2019-2020-1 20175316 《信息安全系统设计基础》第1-2周学习总结
教材学习内容总结
第一周
GCC编译:
- 预处理:gcc –E hello.c –o hello.i;gcc –E调用cpp
- 编 译:gcc –S hello.i –o hello.s;gcc –S调用ccl
- 汇 编:gcc –c hello.s –o hello.o;gcc -c 调用as
- 链 接:gcc hello.o –o hello ;gcc -o 调用ld
带head.h的头文件编译:需要使用"-I + 头文件路径"
例:gcc -I include src/*.c -o bin/xx注意使用GCC编译时要加“-g”参数
GDB基本命令
- gdb programm(启动GDB)
- b 设断点(要会设4种断点:行断点、函数断点、条件断点、临时断点)
- run 开始运行程序
- bt 打印函数调用堆栈
- p 查看变量值
- c 从当前断点继续运行到下一个断点
- n 单步运行
- s 单步运行
- quit 退出GDB
大写“K”可以用来查找函数的帮助信息:查看 man page,命令模式下,将光标放在函数名上,按"K"可以直接察看 man page。
断点调试:
break x (x表示设置断点位置的行号)
delete x (x表示删除断点的行号)
list 显示带行数的代码
start+cotinue=run 运行
s+c=r
watch b 观察变量b的值,变化时程序停止
s 进入函数内部
n 单步调试
quit 退出gdb
info b 查看断点信息并保存
save breakpoint fig.dp 保存断点到fig.dp中
gdb hello2 -x fig.dp 调试时读取保存断点文件
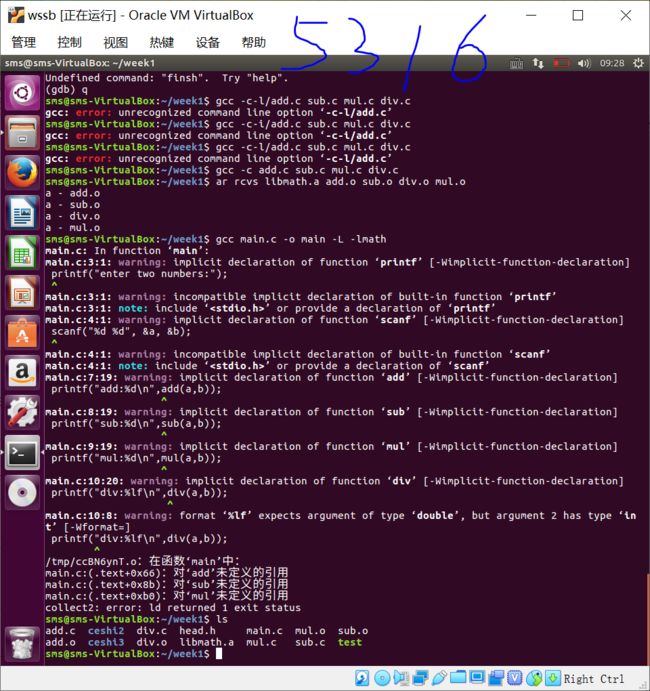
静态库的生成
例:
1、输入 "gcc (-g) -c -I/头文件所在路径 add.c sub.c mul.c div.c" 生成.o文件
2、输入 "ar rcvs libmath.a add.o sub.o mul.o div.o"生成静态库
3、输入 "gcc (-g) main.c -o main -I/头文件所在路径 -L. -lmath" 生成可执行文件main
注意: -I参数用来指定程序要链接的库,-I参数紧接着就是库名
-L参数跟着的是库文件所在的目录名
gcc会在静态库名前加上前缀lib,然后追加扩展名.a得到静态库文件名来查找静态库文件
动态库的生成
例:
1、输入 "gcc (-g) -fPIC -c -I/头文件所在路径 add.c sub.c mul.c div.c" 生成.o文件
2、输入 "gcc -shared -o libmath.so add.o sub.o mul.o div.o"生成动态库
3、将文件libmath.so复制到目录/usr/lib中后,再输入"gcc (-g) main.c -o main -I/头文件所在路径 -L. -lmath"生成可执行文件main
Makefile文件的书写格式:
vim Makefile
文件类型:由哪个文件得到
得到过程
例如:
main:main.o //可执行文件main是由目标文件main.o得到。
gcc main.o –o main //得到过程是将main.o编译成main文件。
main.o:main.c
gcc -c main.c -o main.o 在Makefile文件中一定要将每一个.c文件按执行顺序先编译成.o文件,再按顺序将.o文件编译成可执行文件。
每次编译过后会产生很多的.o文件,对于程序运行没什么太大意义,反而会占内存,所以我们也可以在Makefile文件中添加清除命令(clean),如:
.PHONY:clean
clean: 删除所有文件类型为.o的文件
rm –rf *.o
编译和执行(make:编译, 。/all:执行)
代码调试中的问题和解决过程
- 问题1:在编译时,报错"ld returned 1 exit status"
- 问题1解决方案:在查找资料后,指示编译方式或编译指令有误。最后发现是指令中的I与小写L混淆了。
- 问题2:在做测试的时候,不会使用GDB设置断点
- 问题2解决方案:在参考linux c之gdb常用断点调试总结,学习了(条件)断点的设置和保存,以及一些简单的GDB指令。
- 问题3:GDB调试问题“No source file named file.c. Make breakpoint pending on future shared library load?”和“没有符号表被读取。请使用"file" 命令”
- 问题3解决方案:在编译的时候,没有加-g的选项,导致没有产生调试符号。


第二周
- 无符号编码基于传统的二进制表示法,表示大于或等于0的数字。补码编码是表示有符号整数最常见的方式,有符号整数是可以为正货为负的数字。浮点数编码是表示实数的科学计数法的以2为基数的版本。
- 大多数64位机器可以运行32位机器编译的程序,这是一种向后兼容。例如,当程序prog.c用如下伪指令编译gcc -m32 prog.c该程序就可以在32位或64位机器上正确运行;而该程序用gcc -m64 prog.c运行后,只能在64位机器上运行。
- 小端法:高对高,低对对;大端法:从视觉上,是这次阅读的顺序,与小端法相反。使字节顺序变得可见的三种方式:不同类型的机器之间通过网络传送二进制数据时,网络应用程序的代码编写必须遵守已建立的关于字节顺序的规则;使用反汇编器,处理整数数据的字节序列的存储字节顺序问题;当编写规避正常的类型系统的程序时。
- 逻辑运算容易与位运算相混淆,但他们的功能是完全不同的。逻辑运算认为所有非零的参数都表示true,而参数0表示false。他们返回0或1,分别表示结果为true或false。而按位运算只有在特殊情况下,也就是参数被限制为0或1时,才和与其对应的逻辑运算有相同的的行为。
位运算:
|:或
&:与
~:取反
^:异或 逻辑运算:
逻辑运算符:||(或)、&&(与)、!(非) - 要用C99中的“long long”类型,编译时要用gcc -std=c99
- 有符号数和无符号数之间的转换:
处理同样字长的有符号数和无符号数之间相互转换的一般规则:
数值可能会改变,但是位模式不变。
c语言允许无符号数和有符号数之间的转换。转换的原则是底层的位表示不变。
当从无符号数转换为有符号数是,效果是应用函数U2T,从有符号数转化为无符号数时,应用函数T2U,其中w表示数据类型的位数。
负数和正数相等的情况:u=2147483648 =-2147483648
(当输出分别为无符号形式和有符号形式时)- 在负数x后加上U,可以使其转换为(2^w+x),就可以让负数等于正数
- 对于范围-2^(w-1)≤x<-2^(w-1)内的x,补码的非运算如下:
1.x=-2^(w-1):补码的非为-2^(w-1)
2.x>-2^(w-1):补码的非为-x - 求位级补码非的方法:
对每一位求补,再对结果加1
建立在将位向量分为两部分的基础之上的- 无符号乘法:
两个数x、y相乘且x、y的位数为w,则结果的位数为2w。- 补码乘法:
同无符号乘法。 若为截断后的结果,则取结果的后w位作为计算结果。
注意:无符号运算和补码运算在“+”、“-”、“*”在位级上有相同的结果。- IEEE浮点数表示:
表示形式为:V = (-1)^s * M * 2^E
符号:s决定这个数是负数(s = 1)还是正数(s = 0),而对于数值0的符号位解释作为特殊情况处理。
尾数:M是一个二进制小数,它的范围是1 ~ 2-ε,或者是0 ~ 1-ε。
阶码:E的作用是对浮点数据加权,这个权重是2的E次幂(可能是负数)。
根据阶码的值,可分为一下三种情况:
情况一:规格化的值 (当阶码字段不全为0或全为1时)
E = e-Bias
Bias = 2^(k-1)-1
M = 1+f
情况二:非规格化的值 (当阶码字段全为0时)
E = 1-Bias
Bias = 2^(k-1)-1
M = f
情况三:特殊值 (当阶码字段全为1时)
当小数域全为0时, 当s=1时,为-∞;当s=0时,为+∞。
当小数域不全为0时,为NaN。浮点数的舍入
有四种情况分别是:
向偶数舍入(默认) 向零舍入 向下舍入 向上舍入- 浮点运算
浮点加法:不满足结合性、满足单调性
浮点乘法:不满足结合性、满足单调性,在加法上不满足分配性教材学习中的问题和解决过程
问题1:
length=0时会出现存储器错误,这是因为参数length是无符号的,计算0-1将进行无符号运算,等价于模数加法,结果得到UMax。因为任何数都是小于等于UMax的,所以<=比较总是为真,代码将访问数组a的非法元素。问题1解决方案:
将length声明为int类型
将for循环测试条件改为i>length
上周考试错题总结
- 错题1
第一题没有做出来
其他(感悟、思考等,可选)
- 在学习本门课程的第一周,就对忘了很多的C语言进行了深入的学习。比如编译这一步骤,之前只会用codeblock等点一下就编译了,而没想过中间还需要预处理等步骤,最后还要链接可执行程序。让我有了很大的收获,尤其是刚刚学习的静态库、动态库,让我对C有了新的认识。在这之前,我对Makefile一点认识都没有,在编写Makefile时遇到了一些困难,不论是格式还是编写规则,都是十分新鲜的事物。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 500/1000 | 3/7 | 22/60 |