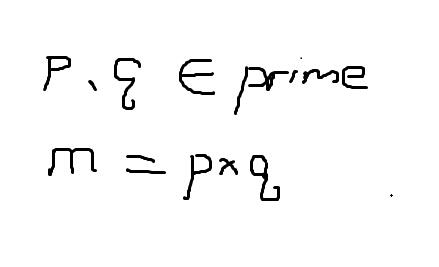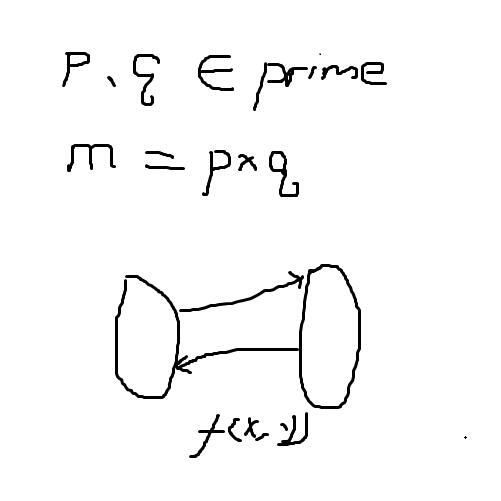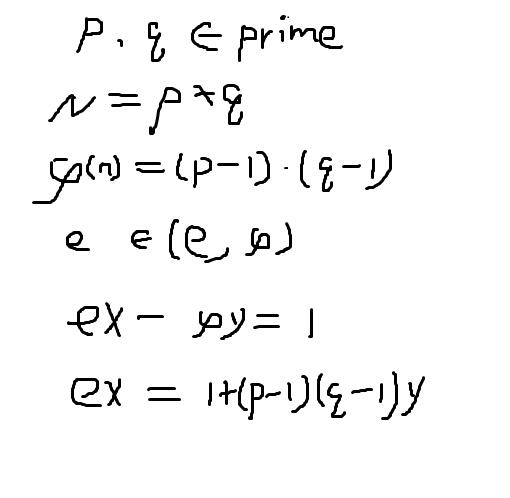同一个密钥可以同时用作信息的加密和解密,这种加密方法称为对称加密。
1975年以前,世界上所有的加密方式都是基于这种的加密方式进行加密。
然而这种对称加密方法的最大问题在于,不管说是发送方还是接收方,这两端都完完全全了解这个密码是个怎么加密与解密的。 所以说第三方如果有心的话,他可以去入侵这两端中的任意一端,他只要成功拿到这个解码或者编码的过程,他就可以破译这个密码。 所有的加密内容对他来说就是没有意义的。
1975年的时候呢,就有人提出一个观念 公钥 ( public key ),这个观念之所以在密码学上是一大进步的原因在于,这个时候,全世界知道怎么解这个密码的人,只有我一个人,我的接收方,我的亲戚朋友,他们拿到的都是公钥。 他们拿到公钥后,等于说是知道了怎么去做这个密码,但是他们没有私钥的情况下是不知道怎么去解这个密码的, 私钥牢牢地掌握在我的手里。 只要我私钥不被窃取,整个加密就是安全的。
公钥与私钥只是一个想法,怎么样去落实呢?
数学家们已经想到了一个方法,就是利用质数的同余的性质
p和q都是代表质数,p和q是很大很大的质数, 那么p*q呢就会变成一个很大很大的数m
请注意,如果我们知道p和q,想要得到m很容易,但是如果我们不知道p和q,想要从一个很大很大的数m中反推出p和q是极端极端困难的,在数学上面,截至目前,都没有找到大数分解的一般算法。
对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用RSA加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA钥匙才可能被强力方式解破。到目前为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被解破的。
RSA 公钥演算法
我们接下来要介绍的这种RSA公钥演算法,是在1977年由MIT的三位数学家提出来的。
Ron Rivest 、 Adi Shamir 、 Leonard Adleman
这三位数学家为公钥演算法找到的一个法宝,就是同余。
我们知道,传统的密码演算法,有点像是函数之间的映射关系。
也就是说呢,我在这边找到一个明文,我通过某种加密方式得到密文,将密文发送给接收方,接收方再进行反演算法,推出的原文。
但是同余的观念完全不是这个样式,同余的观念有点像是一个单方向的转盘,它只能往这边转,不能倒过来转。
什么意思呢? 就是说,我取两个数相乘,模掉19,比如说余数是5, 因为无穷多个自然数相乘模掉19都可能同余5 (mod 19), 所以由同余5 (mod19 ) 反过来推哪两个数相乘,是推不出来的。
所以说RSA公钥演算法,最重要的关键就是它事先透过一种更抽象的分析,我分析说我要再多转几次就可以把原来的资讯转回来。
因为同余就是一种圆运算。 转转转转转,终有一天会把你转回来。
废话这么多,下面就开始正式介绍 RSA公钥演算法。
第一步呢,先找两个非常非常大的质数,p和q,
第二步,p和q相乘得到一个很大很大的数N
下面引入一个很重要的函数,欧拉函数,就是 φ(n)=(p-1)(q-1)
这个φ(n)表示不大于N,并且与N互质的自然数的个数。
以6来举例,
6=2x3
φ(n)=(2-1)(3-1)=2
比6小,并且与6互质的自然数 1,2,3,4,5中 只有1和5,
2个
有了这个 φ(n)之后呢,我就能找到一个 e小于 φ(n),使得e与φ(n)互质。
以21来举例
21=3*7
φ(n)=(3-1)(7-1)=12
表示比21小,并且与21互质的自然数由12个,
分别是 1,2,4,5,8,10,11,12,13,17,19,20
那么我这里就能找到一个5,比φ(n)小,并且与φ(n)互质。
找到e和φ(n)之后, 因为e和φ(n)互质,那么由辗转相除法,我就一定能找到x和y,使得下面等式成立:
ex-φy=1
举例
5和12互质, 那么我就一定能找到x和y使得上面 ex-φy=1 等式成立
5*5-2*12=1
3和7互质
3*5-2*7=1
等等...
这是一个定理。
RSA公钥演算法的精髓就在上面这个等式里面:
ex=1+(p-1)(q-1)
在这个等式里面,x就是我的私钥,我对外发布的公钥是N和e,至于y管都不用管
私钥是只有我一个人才有的,我装在裤衩里任何人都不给看。
公钥等同于说是我向外发出去的一本配钥匙指南,公钥任何人都能看到。
我对外发布N和e,我自己手中留有的是x
实物上的运作
假设你朋友想要发送一段信息给你,这段信息经过编码后呢,就会变成一串数字 A, 什么叫公钥,公钥就是全世界都看得到的两个数字,e和N ,你朋友拿着你给他的公钥e和N,将数字A进行e次方运算, 再去模N,
(前面提到,这个N是个非常非常大的数。由p*q得到。)
你朋友得到这个R之后,全世界的人都知道这个R,也都知道N和e,但是反推出来A是不可能的,因为他们没有私钥,私钥x在你手上。 同余的运算更像是单方向的转盘,抽象理解没有私钥的情况下就不知道转到哪一波,从而就无法得知这个A
你朋友运算后得到的余数 R,将R发送给你,那么你拿出你的私钥x, 将你朋友发送给你的这个R进行x次方运算,再去模掉N,得到的余数A就是你朋友想要发送给你的信息。
实例
在上面的实例中,我找到了一组公钥与私钥,我自保留着私钥x,就是上面的2753,任何人都不给。
我对外发布的是公钥 e和N,这个e和N是全世界的人都能看到的。
如上图所示,A=123是我朋友想要传递给我的信息,经过我的公钥加密后,变成了 855, 我这边通过私钥解密后得到了信息123
(图中蓝色的是公钥,红色的是私钥。)
证明过程,下回分解!