原文地址
写这些的目的是为了做自己的学习笔记,建立自己的知识库。
概念
diffuse 漫反射
ambient 环境; 周围的,包围着的; 产生轻松氛围的;
specular reflection 镜面反射光
directional lights 定向光源
spotlights 点光源
attenuation 变薄; 弄细; 稀薄化; 减少;
Phong reflection model:如下图片解释的够清楚了吧
环境光+漫反射+高光 环境光觉得更应该理解为固有色;
颜色理论
Using only three colors of light, we can make eight different colors: red, green, blue, yellow, cyan, magenta, black and white.
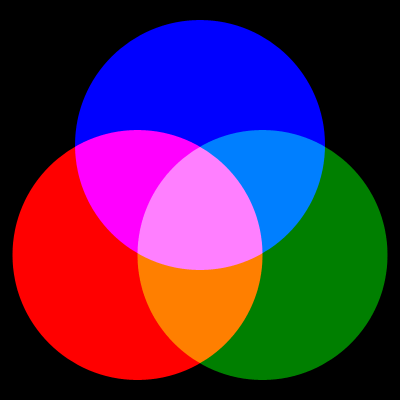
RGB三色光满强度,在白纸上产生8种颜色如图
颜色1
But what about the other colors, like orange? Well, if you take the green light and make it half as bright as it used to be, you would see the image below.
绿光亮度减半后
Lowering the intensity (a.k.a. brightness) of the green has made a few new colors: dark green, sky blue, orange, and pink.
降低绿光强度(亮度),产生了新的颜色:深绿、天蓝、粉红;
Absorption & Reflection Of Color
颜色吸收与反射
If you look at the RGB value of each color, you will notice that the values represent reflectance. (0,0,0) is black, which means reflect none of the light. (1,1,1) is white, which means reflect all of the light. (1,0,0) is red, which means only reflect the red. Cyan is (0,1,1), which means only reflect blue and green. The RGB color of a surface represents how light is absorbed and reflected by that surface.
Calculating the reflected color is simple. The basic formula is:
intensities × surface color = reflected intensities
cyan light × magenta surface = blue light
线性代数计算
(0, 1, 1) × (1, 0, 1) = (0, 0, 1);
Angle of Incidence( 入射角)
决定了表面(看起来)的亮度
If we represent the brightness as a single number, where 0.0 is completely dark and 1.0 is maximum brightness, then it's easy to calculate based on the cosine of the AoI. The formula is brightness = cos(AoI). Let's have a look at the cosine of some angles, just to prove that it works:
cos( 0°) = 1.00 (100% of maximum brightness)
cos( 5°) = 0.98 ( 98% of maximum brightness)
cos( 45°) = 0.71 ( 71% of maximum brightness)
cos( 85°) = 0.09 ( 9% of maximum brightness)
cos( 90°) = 0.00 (Completely dark)
cos(100°) = -0.17 (Completely dark. Negative value means light is hitting the back side)
Once we have a brightness value between 0 and 1, we can multiply it by the intensities of the reflected light to get the final color for the pixel. Here is an example with cyan light:
brightness × light intensities = final color for pixel
1.0 × (0, 1, 1) = (0, 1, 1) (cyan, unchanged)
0.5 × (0, 1, 1) = (0, 0.5, 0.5) (turquoise, which is darkened cyan)
0.0 × (0, 1, 1) = (0, 0, 0) (black)
This "brightness" value between 0 and 1 is sometimes called the "diffuse coefficient."
Surface Normals(表面法线)
要计算AoI入射光夹角就必须知道表面法线和入射光向量;
N = the surface normal vector
L = a vector from the surface to the light source
θ = the angle of incidence
The vector from the surface to the light source, L, can be calculated with vector subtraction, like so:
L=lightPosition−surfacePosition
Calculating The Angle Between Two Vectors: The Dot Product
dot(v1,v2) == length(v1)*length(v2)*cos(angle)
dot(v1,v2)/(length(v1)*length(v2)) == cos(angle)
acos(dot(v1,v2)/(length(v1)*length(v2))) == angle
float brightness = dot(normal, surfaceToLight) / (length(surfaceToLight) * length(normal));
Matrix Transformation Of Normals
法线的矩阵变换:
法线通常是存在于模型空间的,也就是说是相对于未做任何变换的定点坐标的;而计算时向量是经过了positioned/scaled/rotated这些变换的世界坐标中;
So far, we've only used matrices to transform coordinates. The problem is that normals are not coordinates, they are unit vectors representing directions. Rotation transformations are fine, because the rotating a unit vector results in another unit vector, but scaling or translating a normal will result in an incorrect normal. The solution is to multiply the normals by a different matrix – one that has the translation and scaling parts fixed.
之前只是对坐标用矩阵变换,对向量做矩阵变换时旋转没影响但位移和缩放时就会出问题;
Removing the translation part of a 4x4 matrix is simple: we just remove the 4th column and row, converting it to a 3x3 matrix.
mat3 normalMatrix = transpose(inverse(mat3(model)));
vec3 transformedNormal = normalize(normalMatrix * normal);
#version 150
uniform mat4 camera;
uniform mat4 model;
in vec3 vert;
in vec2 vertTexCoord;
in vec3 vertNormal;
out vec3 fragVert;
out vec2 fragTexCoord;
out vec3 fragNormal;
void main() {
// Pass some variables to the fragment shader
fragTexCoord = vertTexCoord;
fragNormal = vertNormal;
fragVert = vert;
// Apply all matrix transformations to vert
gl_Position = camera * model * vec4(vert, 1);
}
#version 150
uniform mat4 model;
uniform sampler2D tex;
uniform struct Light {
vec3 position;
vec3 intensities; //a.k.a the color of the light
} light;
in vec2 fragTexCoord;
in vec3 fragNormal;
in vec3 fragVert;
out vec4 finalColor;
void main() {
//calculate normal in world coordinates
mat3 normalMatrix = transpose(inverse(mat3(model)));
vec3 normal = normalize(normalMatrix * fragNormal);
//calculate the location of this fragment (pixel) in world coordinates
vec3 fragPosition = vec3(model * vec4(fragVert, 1));
//calculate the vector from this pixels surface to the light source
vec3 surfaceToLight = light.position - fragPosition;
//calculate the cosine of the angle of incidence
float brightness = dot(normal, surfaceToLight) / (length(surfaceToLight) * length(normal));
brightness = clamp(brightness, 0, 1);
//calculate final color of the pixel, based on:
// 1. The angle of incidence: brightness
// 2. The color/intensities of the light: light.intensities
// 3. The texture and texture coord: texture(tex, fragTexCoord)
vec4 surfaceColor = texture(tex, fragTexCoord);
finalColor = vec4(brightness * light.intensities * surfaceColor.rgb, surfaceColor.a);
}