机器学习与神经网络（三）：自适应线性神经元的介绍和Python代码实现

前言：本篇博文主要介绍自适应线性神经元的相关知识，采用理论+代码实践的方式，进行相关的学习。本文首先介绍线性神经元的模型，然后介绍LMS学习规则（最小均方规则），最后通过Python代码实现线性神经元模型，从而给读者一个更加直观的认识。

1、线性神经元模型

这里先说一下，一般我们学习映射问题，都是先从“线性映射”开始，然后深入到“非线性映射”，之间最主要的差别就是映射函数f(x):X---->Y,到底是线性的，还是非线性的。所以，线性神经元模型的激活函数肯定就是线性的。我们首先来看下面的图：（图片均来自网络）

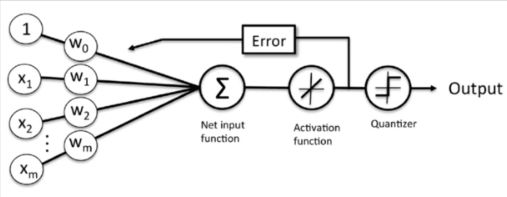
图1：线性神经元模型

解释一下：首先，我们输入训练样本X和初始化权重向量W，将其进行向量的点乘，然后将点乘求和的结果作用于激活函数f(x)=x(典型的线性函数),得到实际的输出O，现在我们根据实际输出O和期望输出d之间的差距error，来调整初始化的权重向量W。如此反复，直到W调整到合适的结果为止。最后在预测阶段，我们就可以使用训练好的W，进行前向传播，即X----->Output的计算，其中的Quantizer可以理解为一个数字转换器，将实际输出压缩到-1到1之间。

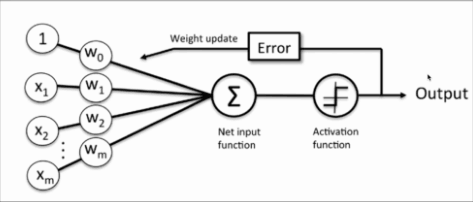
那我们来看看，他与单层感知器模型的差别，比较图1,2，你会发现，他们在结构上非常相似，只是神经元的激活函数不同，由感知器的sign函数变成了purelin函数（f(x)=x）：

图2：单层感知器模型

2.线性神经元的学习规则

有了上面的模型，我们可以看出，他是通过期望输出与实际输出之间的误差进行参数W的调整的，所以介绍一下LMS学习规则如下：

从公式2.26b中可以得出我们权重W的调节程度，那么W=W+△W

3.线性神经元的代码实现

好了，我们已经知道了线性神经元的模型以及相关的学习规则，那么，我们就可以利用Python来实现他（代码基于Python2.7，Anaconda实现）

#! /usr/bin/env python
#coding=utf-8
import numpy as np
import matplotlib.pyplot as plt
#自适应线性神经元类的代码
class AdalineGd(object):
    '''
    eta: float
    学习效率，处于0和1之间
     
    n_iter：int
    对训练数据进行学习，改进次数
     
    w_：一维向量
    存储权重数值
     
    error_：
    一维向量
    存储每次迭代改进时，神经网络对数据进行错误判断的次数
    '''
    def __init__(self,eta = 0.01,n_iter=50):
        self.eta=eta
        self.n_iter =n_iter  
    def fit(self,X,y):
        '''
        :param X: 二维数组[n_samples, n_features]
        n_samples 表示X中含有训练数据条目数
        n_features含有4个数据的一维向量，用于表示一条训练条目
        :param y: 一维向量
        用于存储每一训练条目对应的正确分类
        :return: 
        '''
        self.w_ =np.zeros(1+X.shape[1])#权重初始化为零
        self.cost_ =[]
 
        for i in range(self.n_iter):
            output = self.net_input(X)
            #output=w0+w1*x1+...+wn*xn
            errors = (y - output)#向量，!!!!!!!这里没有用预测predict()
            self.w_[1:]+=self.eta *X.T.dot(errors)
            self.w_[0] +=self.eta *errors.sum()
            cost  =(errors **2).sum()/2
            self.cost_.append(cost)
        return self
 
 
    def net_input(self,X):
        return  np.dot(X,self.w_[1:]+self.w_[0])
 
    def activation(self,X):#线性函数f(x)=x
        return self.net_input(X)
 
    def predict(self,X):#最后的quantizer数字转化器
        return np.where(self.activation(X)>=0,1,-1)
 
 #后面的基本就是为了测试代码，并且进行可视化展示
import pandas as pd
file = 'Iris.csv'
df = pd.read_csv(file,header=None)
y = df.loc[0:100,4].values
y=np.where(y=='Iris-setosa',-1,1)
#根据整数位置选取单列或单行数据
X = df.loc[0:100,[0,2]].values
 
from matplotlib.colors import ListedColormap
def plot_decision_region(X,y,classifier,resolution=0.02):
    markers=('s','x','o','v')
    colors=('red','blue','lightgreen','gray','cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
 
    x1_min ,x1_max = X[:,0].min()-1,X[:,0].max()
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max()
    xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
                      np.arange(x2_min, x2_max, resolution))
    #得到预测分类输出
    Z =classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    print (xx1.ravel())
    print(xx2.ravel())
    print Z
    Z=Z.reshape(xx1.shape)
    plt.contourf(xx1,xx2,Z,alpha =0.4, cmap=cmap)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())
    for idx,cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y==cl,0],y=X[y==cl,1],alpha=0.8,c=cmap(idx),
                    marker=markers[idx],label=cl)
 #这里开始训练
ada = AdalineGd(eta=0.0001,n_iter=100)

ada.fit(X,y)
#这里开始使用predict()并且一些可视化操作
plot_decision_region(X,y,classifier=ada)
plt.xlabel('huajingchang')
plt.ylabel('huabanchang')
plt.legend(loc='upper left')
plt.show()
 
 #可视化W调整的过程中，错误率随迭代次数的变化
plt.plot(range(1,len(ada.cost_)+1),ada.cost_,marker ='o')
plt.xlabel('epochs')
plt.ylabel('sum-squard-error')
plt.show()

实验截图如下：

最后：图片如有侵权，望告知，删。如有错误之处，还望指正。