深度学习(8)——无监督语义分割之全卷积域适应网络(FCAN)
深度学习(8)——无监督语义分割之全卷积域适应网络(FCAN)
Fully Convolutional Adaptation Networks for Semantic Segmentation
篇文章发表在CVPR2018上,主要工作是提出了两种域适应策略,探索了如何使用合成图像提升真实图像的语义分割性能。
讲解论文之前,我们先来看几个概念。
域适应(Domain adaptation):
域适应问题(域自适应问题)中包含两个域,一个包含大量的标签信息,称为源域(source domain);另一个只有少量的甚至没有标签,但是却包含我们要预测的样本 ,称为目标域(target domain)。源域和目标域的数据分布不同,相关但不相同,如猫和虎两个数据集。如何使得源域(Source Domain)上训练好的分类器能够很好地迁移到没有标签数据的目标域上(Target Domain)上,这种迁移学习叫做域适应。
Domain shift:
源域和目标域的数据分布存在巨大的偏差。
了解这两个概念后,我们来看一下这篇文章的背景介绍。
现在获取大量有标签的数据很困难,特别是用于图像分割的像素级标记信息更困难。于是有学者提出通过游戏引擎合成自动驾驶场景下的图像数据,同时得到像素级的语义标签。但是合成图像和真实图像之间存在domain shift问题,这篇文章就是探索这个问题。
相关工作
这篇文章是基于全卷积适应网络的语义分割,所以相关工作分为语义分割和域适应
语义分割的目的是预测给定图像或视频帧的像素级语义标签。最近阶段的工作大都是基于FCN,如包括多尺度特征融合提出的背景信息保存,或用条件随机场等改进FCN;还有使用弱监督进行语义分割。
域适应现在主要的工作方向是无监督、监督和半监督自适应,主要划分依据就是目标域的标记数据是否可用。
这篇文章的主要工作集中在语义分割的无监督自适应。
Method
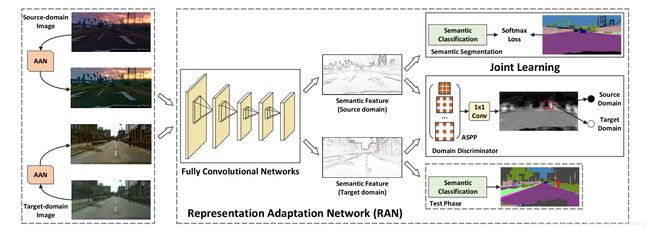
FCAN(全卷积自适应网络)有两个组成部分,左侧的图像域适应网络(AAN),从appearance-level角度处理图像,实际上这部分就是图像风格转换,使得源域图像和目标域图像更加相近。右侧是特征适应网络(RAN),从representation-level角度进行语义分割,实际上就是GANs。其中源域图像是游戏引擎合成图像,目标域是真实街道场景。

AAN结构如上图,它的的作用是将目标域和源域的图像进行预处理,先进行风格转换。将白噪声输入网络,以迭代的方式,通过网络深层的feature correlation,也就是Gram矩阵和目标域图像集合 X t X_t Xt 的深层的feature correlation更相近来约束图像风格,网络浅层的feature map和源域图像 X s X_s Xs 的feature map相近,来约束图像的语义内容,从而实现 X s X_s Xs 到 X t X_t Xt 的转换,得到自适应图像 x o x_o xo,让游戏引擎合成图像看起来更像真实街道图象。
首先使用预训练好的网络训练每一张图像得到feature map,假设每个卷积层 l l l具有 N l N_l Nl个feature map,并且每个feature map的大小是 H l × W l H_l \times W_l Hl×Wl ,那么 l l l层的feature map可以表示为 M l ∈ R N l × H l × W l M^l \in {\Bbb R}^{N_l×H_l×W_l} Ml∈RNl×Hl×Wl
L c o n t e n t = min x o ∑ l ∈ L w s l D i s t ( M o l , M s l ) L_{content} = \min_{x_o} \sum_{l \in L} w^l_s Dist(M^l_o , M^l_s) Lcontent=xominl∈L∑wslDist(Mol,Msl)
上式是关于来自源域图像 X s X_s Xs和自适应输出图像 X o X_o Xo的风格损失函数。取网络训练后几层的feature map,最小化相关图层feature map的欧式距离,训练图层的权重 w s l w^l_s wsl , 得到关于语义内容的损失函数。
对于图像风格的计算是通过Gram矩阵计算相关层feature map像素点之间的协方差矩阵,忽略其之间的空间信息,只保留像素点之间的相关性。
G l , i j = M l , i ⨀ M l , j G^{l,ij} = M^{l,i} \bigodot M^{l,j} Gl,ij=Ml,i⨀Ml,j
和普通图像风格转换不同的是,目标域的输入 X t X_t Xt是一组图像,而源域图像是一张图像 X s X_s Xs。我们将对应层得到的矩阵 G l G^l Gl求平均 G ‾ t l {\overline G}^l_t Gtl,将一张图像的风格拓展到一个域中的风格。
L s t y l e = min x o ∑ l ∈ L w t l D i s t ( G o l , G ‾ t l ) L_{style} = \min_{x_o} \sum_{l\in L}w^l_t Dist(G^l_o , {\overline G}^l_t) Lstyle=xominl∈L∑wtlDist(Gol,Gtl)
同样最小化相关图层的矩阵 G G G ,训练图层权重 w t l w^l_t wtl ,得到关于图像风格的损失函数。
最后总的损失函数是, α \alpha α 取值是 1 0 − 14 10^{-14} 10−14 ,手动设定(因为最终要进行语义分割,所以 α \alpha α 设置很小)
KaTeX parse error: Expected '}', got '\cal' at position 18: …_{AAN}(x_o) = {\̲c̲a̲l̲ ̲L}_{content} + …
在每次迭代 i i i中,图像 x o x_o xo由 x o i − 1 − w i − 1 g i − 1 ∣ ∣ g i − 1 ∣ ∣ 1 x^{i-1}_o - w^{i-1}\frac{g^{i-1}}{\mid\mid g^{i-1} \mid\mid_1} xoi−1−wi−1∣∣gi−1∣∣1gi−1 更新,其中 g i − 1 = ∂ L a p p ( x o i − 1 ) ∂ x o i − 1 , w i − 1 = β I − i I , a n d β = 10 g^{i-1} = \frac{\partial L_{app}(x^{i-1}_o)}{\partial x^{i-1}_o} , w^{i-1} = \beta \frac{I-i}{I} , and \quad \beta = 10 gi−1=∂xoi−1∂Lapp(xoi−1),wi−1=βII−i,andβ=10。
RAN 的结构图如上,实质是一个对抗网络。
将经过AAN的源域图像和目标域图像输入RAN,利用共享的FCN提取特征,使用最后一个卷积层的feature map。
这里先介绍下什么是扩张卷积(也叫空洞卷积),扩张卷积是具有一个扩张因子的常规卷积。首先根据扩张因子对卷积滤波器进行扩张,然后用0填充空白空间,最后使用扩张的滤波器进行常规卷积。
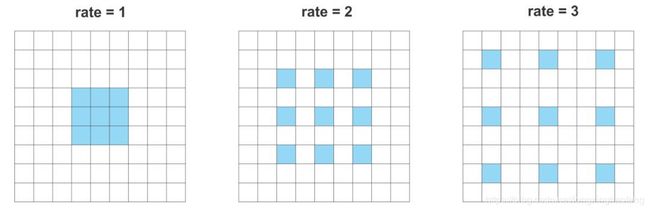
在对抗分支这里有一个概念,叫ASPP,空洞空间金字塔池化。并行计算了4个 3 × 3 × 128 3\times 3\times 128 3×3×128的扩张卷积层,扩张率分别为1,2,3,4。将4个特征图堆叠在一起,形成有128*4个信道的特征图,再用 1 × 1 1\times 1 1×1 的卷积层,接上sigmoid层生成分割逻辑。
这是空洞空间金字塔池化,还有一种池化是金字塔池化。

如上图,在最后一层卷积层后,全连接层前加入一层 spatial pyramid pooling layer(金字塔池化层)。其实就是三个并行的pooling,池化窗口和步长由feature map决定,最终三个pooling输出分别是$4 \times 4 ,2 \times 2 ,1 \times 1 $ ,合成一个向量 1 × 21 1 \times 21 1×21,图中的256是信道数。
假设经过最后一层卷积得到的feature map的大小是 a × a a \times a a×a ,我们想得到的池化视图大小是 n × n n \times n n×n ,那么池化窗口为 ⌈ a n ⌉ \left\lceil \frac{a}{n} \right\rceil ⌈na⌉ , 步长为 ⌊ a n ⌋ \left\lfloor\ \frac{a}{n} \right\rfloor ⌊ na⌋
原文中解释这样做扩充了FCN的输出,实际上也起到多尺度融合的作用,对不同尺度的图像都使用该网络。
空洞空间金字塔池化在对抗分支应用,金字塔池化在分割分支中应用。
通过FECN,我们得到源域中的训练集 X s = { x s i ∣ i = 1 , … , n } X_s = \left\{ x^i_s \mid i = 1,\dots ,n \right\} Xs={xsi∣i=1,…,n}和目标域中的 X t = { x t i ∣ i = 1 , … , m } X_t = \left\{ x^i_t \mid i = 1,\dots ,m \right\} Xt={xti∣i=1,…,m} ,对抗网络的Loss是:
L a d v ( X s , X t ) = − E x t ∼ X t [ 1 Z ∑ i = 1 Z log ( D i ( F ( x t ) ) ) ] − E x s ∼ X s [ 1 Z ∑ i = 1 Z log ( 1 − D i ( F ( x s ) ) ) ] L_{adv}(X_s,X_t) = -E_{x_t \sim X_t}[\frac{1}{Z}\sum^Z_{i=1}\log (D_i(F(x_t)))] -E_{x_s \sim X_s}[\frac{1}{Z}\sum^Z_{i=1}\log (1 - D_i(F(x_s)))] Ladv(Xs,Xt)=−Ext∼Xt[Z1i=1∑Zlog(Di(F(xt)))]−Exs∼Xs[Z1i=1∑Zlog(1−Di(F(xs)))]
其中 Z Z Z是 D D D输出中空间单位的数量。与标准GANs类似,我们的RAN的对抗训练是优化以下最小极大函数
max F min D L a d v ( X s , X t ) \max_F \min_D L_{adv}( X_s , X_t) FmaxDminLadv(Xs,Xt)
同时优化标准像素级分类损失 L s e g L_{seg} Lseg,用于来自源域的图像的监督分割,其中标签可用。因此,RAN的总体目标是将 L s e g L_{seg} Lseg和 L a d v L_{adv} Ladv整合为
max F min D { L a d v ( X s , X t ) − λ L s e g ( X s } \max_F \min_D \left\{ L_{adv}(X_s , X_t) - \lambda L_{seg} (X_s \right\} FmaxDmin{Ladv(Xs,Xt)−λLseg(Xs}
其中 λ \lambda λ 是平衡参数。
先预训练只有分割Loss的RAN,然后设置 λ = 5 \lambda = 5 λ=5 ,加入对抗Loss联合训练。
实验
文章对来自GTA5 (游戏视频)数据集到城市景观(城市街景)数据集的域适应性进行了实验。GTA5数据集是游戏侠盗猎车手游戏里的图像,城市街景用的Cityscapes数据集。
分别对AAN和RAN部分进行了实验,在所有实验中,采用每个类别的联合交叉(IoU),并将所有类别的IoU表示为性能指标。
AAN部分,发现在训练期间用ANN将source domain image转到target domain,然后在测试期间不使用ANN对target domain进行变换,得到的效果最好。
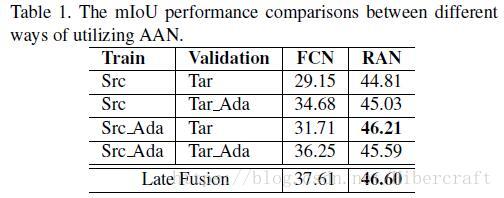
针对RAN部分,文章依次叠加Adaptive Batch Normalization (ABN),Adversarial Domain Adaptation (ADA),使用全卷积网络做decoder(conv),引入ASPP网络,ANN,得到了实验结果如下图。
自适应批量归一化(ABN)简单地将源域中学习的FCN中的BN层的均值和方差替换为在目标域中的图像上计算的BN层的均值和方差。对抗域适应(ADA)利用对抗性训练的思想来学习域不变表示,域判别器在图像级别上判断域。当扩展域判别器以对每个图像区域进行分类时,该设计被命名为Conv。 ASPP进一步扩大了过滤器的视野,以增强对抗性学习。 AAN是我们的appearance-level改编。

与Cityscapes上最先进的无监督域自适应方法的性能比较。
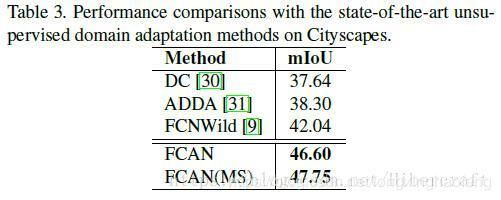
DC和ADDA不太了解,FCNWild仅使用对抗方式进行语义分割的自适应。FCAN基于FCNWild,额外纳入ASPP策略和AAN的强化。多尺度(MS)方案的FCAN性能最佳。多尺度是加入了金字塔池化层。
结论
提出了完全卷积自适应网络(FCAN)架构,该架构探索了语义分割的域自适应。特别是,我们从appearance-level和representation-level适应的角度研究问题。为了验证我们的结论,我们已经在我们的FCAN中分别为每个目的设计了图像适应网络(AAN)和特征适应网络(RAN)。我们未来可能的工作包括两个方向。首先,将在AAN中研究使用另一种统计模式渲染图像的语义内容的更高级技术(即针对AAN部分使用更新的算法进行优化)。其次,我们将进一步将我们的FCAN扩展到其他特定的分割场景,例如室内场景分割或纵向分割,其中可以容易地生成合成数据。
关于“分布”不同的理解:
X,Y分别表示带标签数据的数据以及标签,$P(X,Y) $是X,Y的联合概率分布(joint distribution)
联合概率分布的几何意义为:如果将二维随机变量 ( X , Y ) (X,Y) (X,Y)看成是平面上随机点的坐标,那么分布函数 P ( x , y ) P(x,y) P(x,y)在 ( x , y ) (x,y) (x,y)处的函数值就是随机点 ( X , Y ) (X,Y) (X,Y)落在以点 ( x , y ) (x,y) (x,y)为顶点而位于该点左下方的无穷矩形域内的概率。
P ( X , Y ) s , P ( X , Y ) t P(X,Y)_s,P(X,Y)_t P(X,Y)s,P(X,Y)t 分别对应源域以及目标域的联合分布函数。
P s ( X ) , P s ( Y ) , P t ( X ) , P t ( Y ) P_s(X), P_s(Y), P_t(X), P_t(Y) Ps(X),Ps(Y),Pt(X),Pt(Y)表示源域和目标域中X以及Y的边缘分布(marginal distributions)
某一组概率的加和,叫边缘概率。边缘概率的分布情况,就叫边缘分布。
$ P_s(X|Y), P_s(Y|X), P_t(X|Y), P_t(Y|X)$ 表示X,Y的条件分布。
X = x , Y = y X=x,Y=y X=x,Y=y的联合概率为 P ( X = x , Y = y ) = P ( x , y ) P(X=x,Y=y)=P(x,y) P(X=x,Y=y)=P(x,y)。 x ∈ χ , y ∈ Υ x∈χ,y∈Υ x∈χ,y∈Υ,其中$χ,Υ $表示实例空间以及类标签空间。