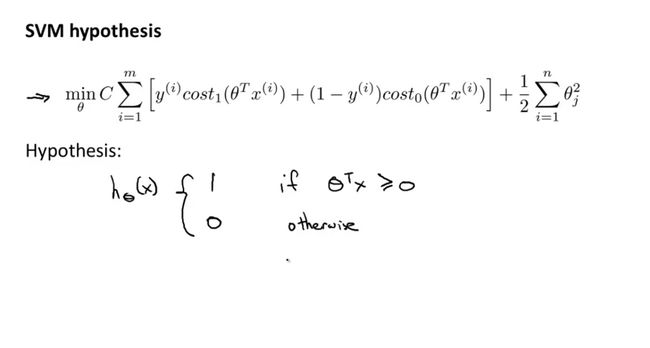【Stanford机器学习笔记】10-Support Vector Machines

这节讲支持向量机在机器学习领域的应用

1. Large Margin Classification

1.1 Optimization Objective

通过逻辑回归的代价函数进行修改得到支持向量机的代价函数，首先定义两个函数：

Cost1(z)Cost0(z)z=θTx

根据逻辑回归模型的代价函数，我们可以得到支持向量机的代价函数及目标函数形式为：

minC∑i=1m[y(i)Cost1(θTx(i))+(1−y(i))Cost0(θTx(i))]+12∑j=1nθ2j

SVM的假设函数是直接通过参数 θ 得出样本所属的类别。

从中可以看出，单个SVM分类器的作用即是把样本分成两个类别，非A即B，不像logistic regression输出的是每个类别的概率大小。

1.2 Large Margin Intuition

（1）SVM又称为最大间隔分类器，由前一节中，我们知道，当 z=θTx 远大于0时，我们就能预测样本属于正样本（y=1），当 z=θTx 远小于0时，我们就能预测样本属于负样本（y=0），根据之前对 Cost1(z) 和 Cost0(z) 的定义，我们现在定义：
当 z=θTx 大于等于1时，我们就能预测样本属于正样本（y=1），当 z=θTx 小于等于-1时，我们就能预测样本属于负样本（y=0），不仅仅大于零活小于零。

（2）现在我们假设一种特殊情况，正则化项C是一个较大的值，例如C=100000；根据SVM的代价函数，

minC∑i=1m[y(i)Cost1(θTx(i))+(1−y(i))Cost0(θTx(i))]+12∑j=1nθ2j

我们可以知道，如果C很大，则我们需要将

∑i=1m[y(i)Cost1(θTx(i))+(1−y(i))Cost0(θTx(i))]=0

所以，我们可以得到当 z=θTx 大于等于1时，我们就能预测样本属于正样本（y=1），当 z=θTx 小于-1时，我们就能预测样本属于负样本（y=0）。
此时，我SVM的代价函数就会变为：

min12∑j=1nθ2jsubject to:θTx≥1 if y=1θTx≤−1 if y=0

此时，我们就会得到一个最大间隔决策边界。

（3）当C较大时，而且当我们的数据集中有异常点是，为了寻求最大间隔分类边界，SVM可能会得出误差较大的决策边界，这时，如果我们把C设置的小一点，则SVM会忽略掉异常点的影像，而且对于一些非线性的分类问题更加适用。

1.3 Mathematics Behind Large Margin Classification

（1）如果想了解SVM是如何寻找最大分类间隔的，需要知道向量内积的概念。假设有两个二维向量u和v：

u=[u1u2]v=[v1v2]

向量内积

uTv=u1v1+u2v2=p∙||u||||u||=u21+u22−−−−−−√表示向量的范数或模

其中p是向量v在向量u上的投影长度，是个实数。介绍向量内积的概念主要是要与 θTx 作类比。

（2）上一节中，我们知道，当我们假设正则化常数C是个很大的值，则SVM的目标函数就是：

min12∑j=1nθ2jsubject to:θTx≥1 if y=1θTx≤−1 if y=0

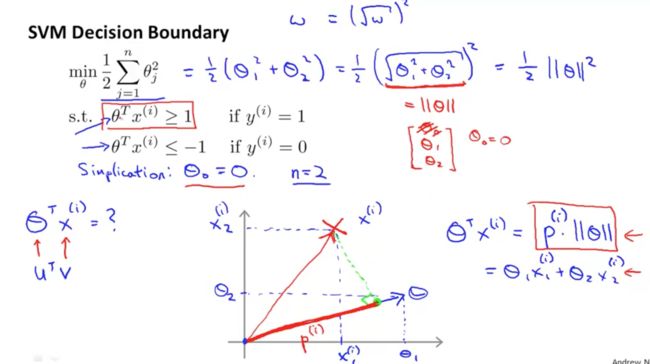
现在我们用向量内积的形式进行表示（为了简化，现假设 θ0=0 and n=2即有两个特征变量 ，便于绘图表示）：

min12∑j=1nθ2j=12(θ21+θ22)=12(θ21+θ22−−−−−−√)2=12||θ||2subject to:θTx=p(i)∙||θ||≥1 if y=1θTx=p(i)∙||θ||≤−1 if y=0

所以现在的优化目标就变成了要最小化 ||θ|| ，根据约束条件可知，如果最小化 ||θ|| ，必须要p最大，即样本到参数向量的投影长度最大，即最大分类间隔。

以上为了简化，都是假设 θ0=0 ,这时决策边界是过原点的，如果 θ0≠0 ,同样可以证明以上过程。

以上的推导都是基于常数C比较大的情况，目标函数为

min12∑j=1nθ2jsubject to:θTx≥1 if y=1θTx≤−1 if y=0

为了求解非线性分类时，需要引入核函数。

2. Kernels

2.1 Kernels I

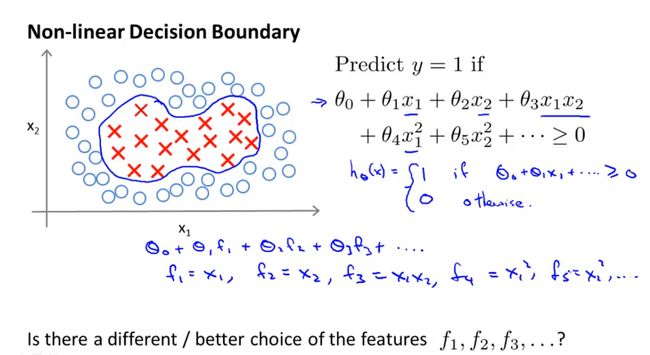
（1）引进核函数是为了解决非线性分类问题，之前在逻辑回归模型中，我们通过构建多项式特征项可以构建出非线性分类器，但是如果有很多特征，就会导致运算很慢。

核函数是另外一种构建新的特征用于解决非线性分类的问题。为了引进核函数，现在定义一系列新的符号代表构建的新的特征集：

f1,f2，f3...fn

（2）首先定义定义三个标记点

l(1),l(2),l(3)

然后利用高斯函数定义三个特征变量 f1,f2，f3 ：

f1=similarity(x,l(1))=k(x,l(1))=exp(−||x−l(1)||22σ2)f2=similarity(x,l(2))=k(x,l(2))=exp(−||x−l(2)||22σ2)f3=similarity(x,l(3))=k(x,l(3))=exp(−||x−l(3)||22σ2)

（3）核函数和相似度函数的含义：

根据以上定义可知

• 如果 x 与 l(1) 很近，则可知 ||x−l(1)||≈0 ,则 f1≈1

• 如果 x 与 l(1) 很远，则可知 ||x−l(1)||≈larger number ,则 f1≈0

  三个标记点定义了三个新的特征。

（4）高斯核函数的图解
高斯核函数的作用就是评估样本与标记点的距离，与标记点距离越近，约等于1，与标记点距离越远，就靠近0，其中另外一个参数 σ2 控制着高斯函数的宽窄，越大则越平缓，越小则越陡峭。

（5）高斯核函数的分类使用
假设已知一组参数向量，

• 如果有一个样点距离标记点 l(1) 比较近，则可以算出 θTf 大于0，该点的类别为y=1；
• 如果有一个样点距离标记点 l(1) 比较远，则可以算出 θTf 小于0，该点的类别为y=0；

通过上述方式，遍历所有样点则可以对样本进行分类。

目前我们还不知道如何选择标记点，以及如何训练参数，下一节将继续阐述。

2.2 Kernels II

（1）如何选择标记样点
机器学习中，一般情况是将样本点直接作为样本点，表示该样本点与其他样本点的距离，即

x(i)=l(i)

这样，我们就一共有m个样点，此时构建的新特征也有n=m个，即

f1,f2,....fm

（2）生成新特征变量
假设有m个训练样本，并选择样本点作为标记点，对于训练样本 (x(i),y(i)) 则有新特征向量：

f(i)1=similarity(x(i),l(1))=k(x(i),l(1))=exp(−||x(i)−l(1)||22σ2)f(i)2=similarity(x(i),l(2))=k(x(i),l(2))=exp(−||x(i)−l(2)||22σ2)f(i)3=similarity(x(i),l(3))=k(x(i),l(3))=exp(−||x(i)−l(3)||22σ2)............f(i)i=similarity(x(i),l(i))=k(x(i),x(i))=exp(−||x(i)−l(3)||22σ2)=1............f(i)m=similarity(x(i),l(3))=k(x(i),l(3))=exp(−||x(i)−l(3)||22σ2)

所以，原来有n个特征的训练样本将转化为有m个新特征的训练样本。

（3）SVM with kernels算法应用流程

• 给定训练样本x
• 确定核函数，根据核函数得出新的特征向量
• 确定假设函数，即模型（ θTf≥0 ，则y=1）
• 最小化代价函数，训练得出参数集
• 代价函数有原始训练样本的
  minC∑i=1m[y(i)Cost1(θTx(i))+(1−y(i))Cost0(θTx(i))]+12∑j=1nθ2j
  变为
  minC∑i=1m[y(i)Cost1(θTf(i))+(1−y(i))Cost0(θTf(i))]+12∑j=1mθ2j

（4）SVM算法的高偏差和高方差的权衡
主要包括正则化常数项C和核函数 σ2 的选择.
对于常数项C，

• 如果C 比较大，则会出现低偏差，高方差
• 如果C比较小，则会出现高偏差，低方差
• 如果 σ2 比较大，则会出现高偏差，低方差
• 如果 σ2 比较小，则会出现低偏差，高方差

理论上讲，核函数是可以用于逻辑函数回归模型中，但是这样的话会使得计算量很大。核函数是专门为SVM设计的。

3. SVMs in Practice

3.1 Using An SVM

（1）为简便计算，一般看利用数值计算库求解参数，但是都需要制定一些特定值：

• 正则化项C
• 核函数类型
  
  • 线性核函数
  • 高斯函数

将训练样本代入高斯函数前需要对特征进行归一化处理。

（2）其他核函数
多项式核函数：

(xl+constant)degree

（3）SVM用于多类别分类问题
假设一共有K类，利用“一对多”的原则，依次训练K个SVM分类器用于每个类别，得到K组参数 θ ,然后将新样本依次代入K个分类器中，选择最大值作为该类别。

（4）逻辑回归模型与SVM
至今，对于分类问题，我们已经学习了逻辑回归模型，神经网络和SVM算法，但是什么时候用什么算法呢？

n	m	algorithm
large	small	logistic Regression or SVM without a kernel
small	intermediate	SVM with Gaussian Kernel
small	large	create/add more features, then use logistic Regression or SVM without a kernel

对于神经网络算法，相对于SVM来说，运行训练较慢，SVM是一种凸优化解，只存在全局最优解，不会出现局部最优解的问题。