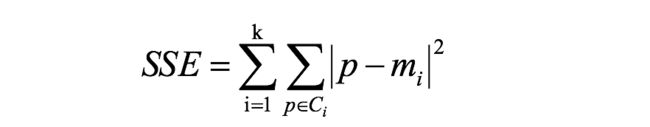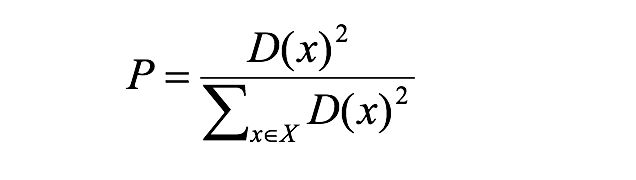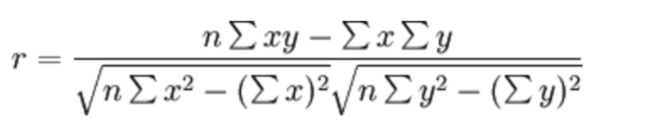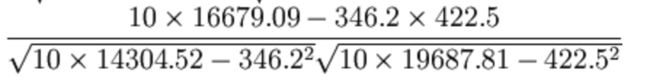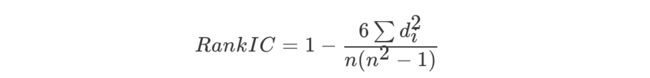机器学习--聚类算法
一.聚类算法简介
认识聚类算法
1.1聚类算法的应用
- 用户画像,广告推荐,Data Segmentation,搜索引擎的流量推荐,恶意流量识别
- 基于位置信息的商业推送,新闻聚类,筛选排序
- 图像分割,降维,识别;离群点检测;信用卡异常消费;发掘相同功能的基因片段
1.2聚类算法的概念
聚类算法:
一种典型的无监督学习算法,主要用于将相似的样本自动归到一个类别中。
在聚类算法中根据样本之间的相似性,将样本划分到不同的类别中,对于不同的相似度计算方法,会得到不同的聚类结果,常用的相似度计算方法有欧式距离法。
1.3聚类算法与分类算法的区别
聚类算法是无监督的学习算法,而分类算法属于监督的学习算法。
二.聚类算法api初识
2.1 api介绍
- sklearn.cluster.KMeans(n_clusters=8)
- 参数:
- n_clusters:开始的聚类中心数量
- 整型,缺省值=8,生成的聚类数,即产生的质心(centroids)数。
- n_clusters:开始的聚类中心数量
- 方法:
- estimator.fit(x)
- estimator.predict(x)
- estimator.fit_predict(x)
- 计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)
- 参数:
2.2案例
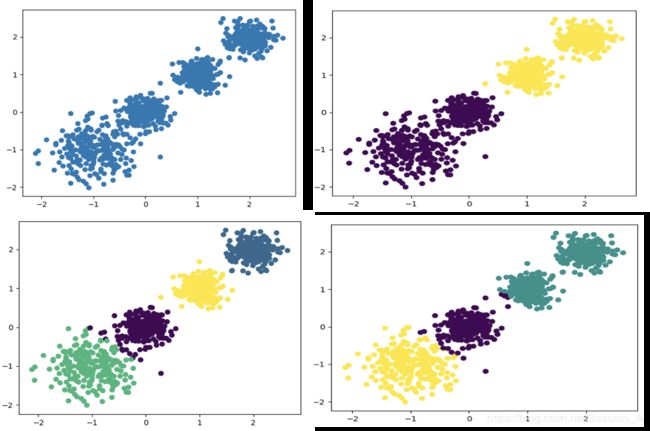
随机创建不同二维数据集作为训练集,并结合k-means算法将其聚类,你可以尝试分别聚类不同数量的簇,并观察聚类效果:
聚类参数n_cluster传值不同,得到的聚类结果不同
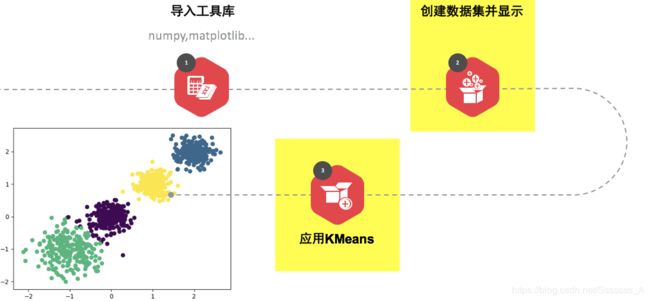
2.2.1流程分析
2.2.2代码实现
-
创建数据集
import matplotlib.pyplot as plt from sklearn.datasets.samples_generator import make_blobs from sklearn.cluster import KMeans from sklearn.metrics import calinski_harabaz_score # 创建数据集 # X为样本特征,Y为样本簇类别, 共1000个样本,每个样本4个特征,共4个簇, # 簇中心在[-1,-1], [0,0],[1,1], [2,2], 簇方差分别为[0.4, 0.2, 0.2, 0.2] X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]], cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=9) # 数据集可视化 plt.scatter(X[:, 0], X[:, 1], marker='o') plt.show() -
使用k-means进行聚类,并使用CH方法评估
y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X) # 分别尝试n_cluses=2\3\4,然后查看聚类效果 plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.show() # 用Calinski-Harabasz Index评估的聚类分数 print(calinski_harabaz_score(X, y_pred))
三.聚类算法实现流程
k-means其实包含两层内容:
K : 初始中心点个数(计划聚类数)
means:求中心点到其他数据点距离的平均值
3.1 k-means聚类步骤
- 随机设置K个特征空间内的点作为初始的聚类中心
- 对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
- 接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
- 如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程
通过下图解释实现流程:
3.2案例
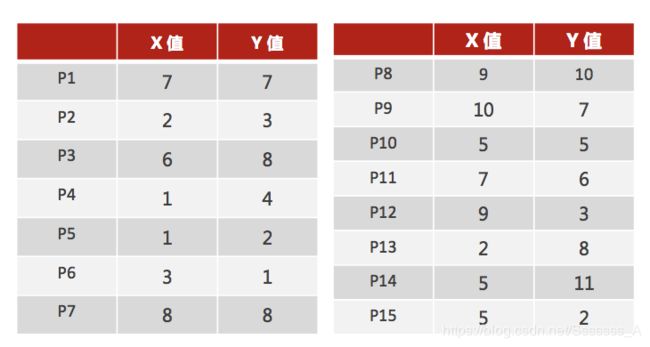
-
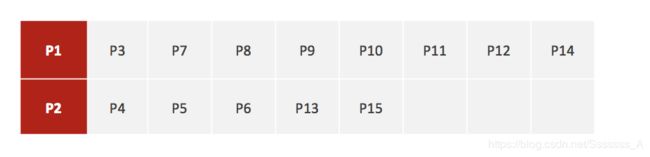
随机设置K个特征空间内的点作为初识的聚类中心(这里选择P1,P2)
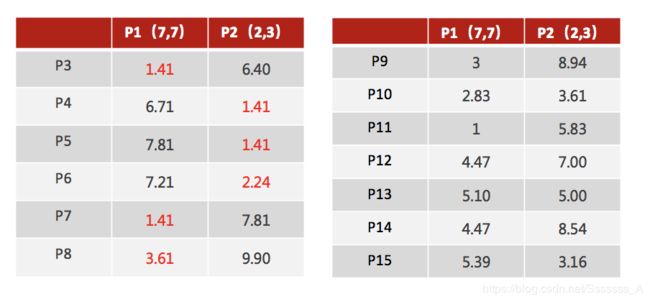
-
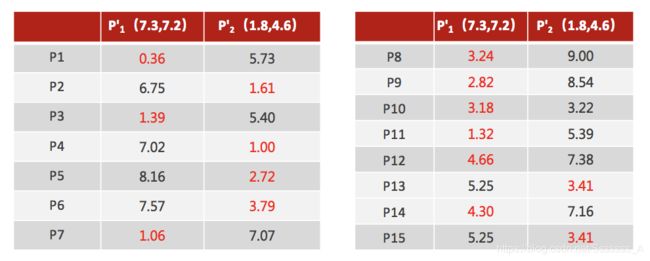
对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
-
接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
-
如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程【经过判断,需要重复上述步骤,开始新一轮迭代】
-
当每次迭代结果不变时,认为算法收敛,聚类完成,K-means一定会停下,不可能陷入一直选质心的过程
3.3总结
流程:
- 事先确定常数K,常数K意味着最终的聚类类别数;
- 首先随机选定初始点为质心,并通过计算每一个样本与质心之间的相似度(这里为欧式距离),将样本点归到最相似的类中,
- 接着,重新计算每个类的质心(即为类中心),重复这样的过程,直到**质心不再改变*
- 最终就确定了每个样本所属的类别以及每个类的质心。
注意:
- 由于每次都要计算所有的样本与每一个质心之间的相似度,故在大规模的数据集上,K-Means算法的收敛速度比较慢。
四.模型评估
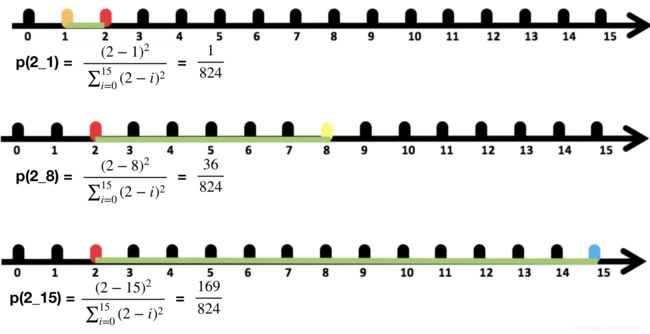
4.1误差平方和
举例:(下图中数据-0.2, 0.4, -0.8, 1.3, -0.7, 均为真实值和预测值的差)
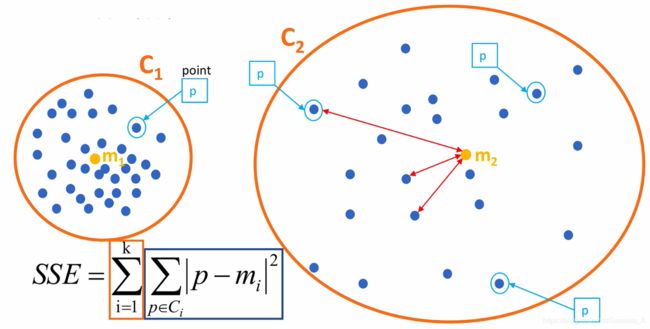
在k-means中的应用:
公式各部分内容:
4.2"肘"方法(Elbow method)-K值确定
-
对于n个点的数据集,迭代计算k from 1 to n,每次聚类完成后计算每个点到其所属的簇中心的距离的平方和;
-
平方和是会逐渐变小的,直到k==n时平方和为0,因为每个点都是它所在的簇中心本身。
-
在这个平方和变化过程中,会出现一个拐点也即“肘”点,下降率突然变缓时即认为是最佳的k值。在决定什么时候停止训练时,肘形判据同样有效,数据通常有更多的噪音,在增加分类无法带来更多回报时,我们停止增加类别。
4.3轮廓系数法
结合了聚类的凝聚度(Cohesion)和分离度(Separation),用于评估聚类的效果:
目的:
内部距离最小化,外部距离最大化
计算样本i到同簇其他样本的平均距离ai,ai 越小样本i的簇内不相似度越小,说明样本i越应该被聚类到该簇。
计算样本i到最近簇Cj 的所有样本的平均距离bij,称样本i与最近簇Cj 的不相似度,定义为样本i的簇间不相似度:bi =min{bi1, bi2, …, bik},bi越大,说明样本i越不属于其他簇。
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。
平均轮廓系数的取值范围为[-1,1],系数越大,聚类效果越好。
簇内样本的距离越近,簇间样本距离越远
案例:
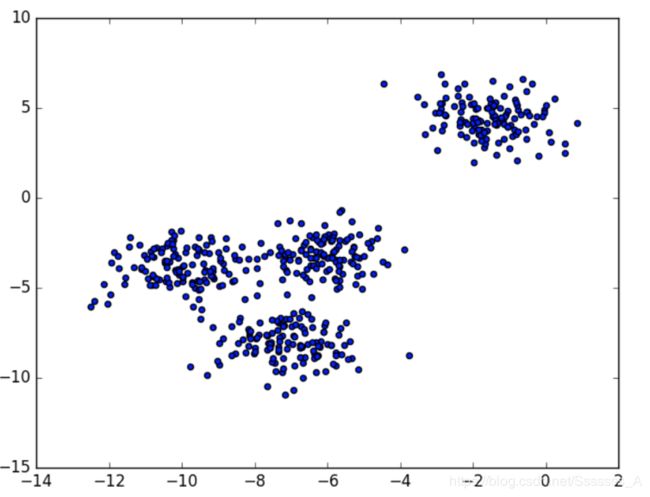
下图是500个样本含有2个feature的数据分布情况,我们对它进行SC系数效果衡量:
n_clusters = 2 The average silhouette_score is : 0.7049787496083262
n_clusters = 3 The average silhouette_score is : 0.5882004012129721
n_clusters = 4 The average silhouette_score is : 0.6505186632729437
n_clusters = 5 The average silhouette_score is : 0.56376469026194
n_clusters = 6 The average silhouette_score is : 0.4504666294372765
n_clusters 分别为 2,3,4,5,6时,SC系数如下,是介于[-1,1]之间的度量指标:
每次聚类后,每个样本都会得到一个轮廓系数,当它为1时,说明这个点与周围簇距离较远,结果非常好,当它为0,说明这个点可能处在两个簇的边界上,当值为负时,暗含该点可能被误分了。
从平均SC系数结果来看,K取3,5,6是不好的,那么2和4呢?
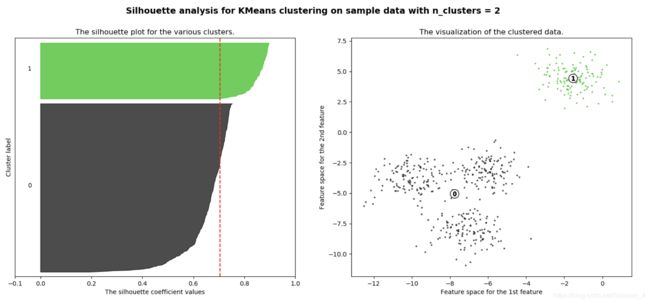
k=2的情况:
k=4的情况:
n_clusters = 2时,第0簇的宽度远宽于第1簇;
n_clusters = 4时,所聚的簇宽度相差不大,因此选择K=4,作为最终聚类个数。
4.4 CH系数
Calinski-Harabasz
类别内部数据的协方差越小越好,类别之间的协方差越大越好(换句话说:类别内部数据的距离平方和越小越好,类别之间的距离平方和越大越好),
这样的Calinski-Harabasz分数s会高,分数s高则聚类效果越好。
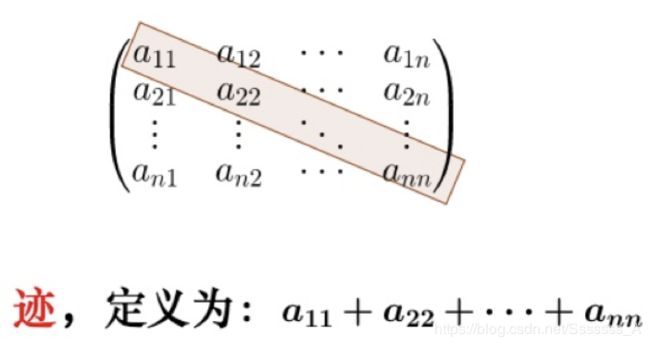
tr为矩阵的迹, Bk为类别之间的协方差矩阵,Wk为类别内部数据的协方差矩阵;
m为训练集样本数,k为类别数。
使用矩阵的迹进行求解的理解:
矩阵的对角线可以表示一个物体的相似性
在机器学习里,主要为了获取数据的特征值,那么就是说,在任何一个矩阵计算出来之后,都可以简单化,只要获取矩阵的迹,就可以表示这一块数据的最重要的特征了,这样就可以把很多无关紧要的数据删除掉,达到简化数据,提高处理速度。
CH需要达到的目的:
用尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果。
4.5总结
1. 肘部法
下降率突然变缓时即认为是最佳的k值
2. SC系数
取值为[-1, 1],其值越大越好
3. CH系数
分数s高则聚类效果越好
五.算法优化
k-means算法小结
优点:
- 原理简单(靠近中心点),实现容易
- 聚类效果中上(依赖K的选择)
- 空间复杂度o(N),时间复杂度o(IKN)
N为样本点个数,K为中心点个数,I为迭代次数
缺点:
- 对离群点,噪声敏感 (中心点易偏移)
- 很难发现大小差别很大的簇及进行增量计算
- 结果不一定是全局最优,只能保证局部最优(与K的个数及初值选取有关)
5.1 Canopy算法配合初始聚类
5.1.1 Canopy算法的实现流程
5.1.2 Canopy算法的优缺点
优点:
- Kmeans对噪声抗干扰较弱,通过Canopy对比,将较小的NumPoint的Cluster直接去掉有利于抗干扰。
- Canopy选择出来的每个Canopy的centerPoint作为K会更精确。
- 只是针对每个Canopy的内做Kmeans聚类,减少相似计算的数量。
缺点:
- 算法中 T1、T2的确定问题 ,依旧可能落入局部最优解
5.2 K-means++
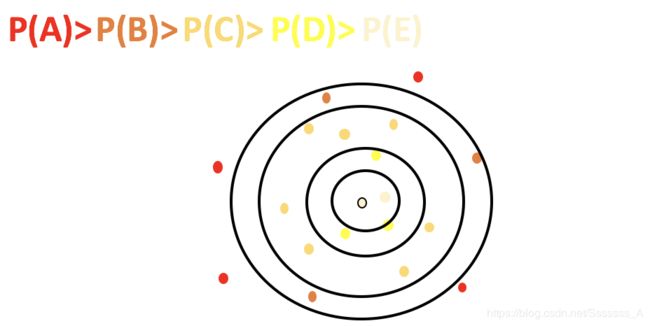
kmeans++目的,让选择的质心尽可能的分散
如下图中,如果第一个质心选择在圆心,那么最优可能选择到的下一个点在P(A)这个区域(根据颜色进行划分)
5.3二分k-means
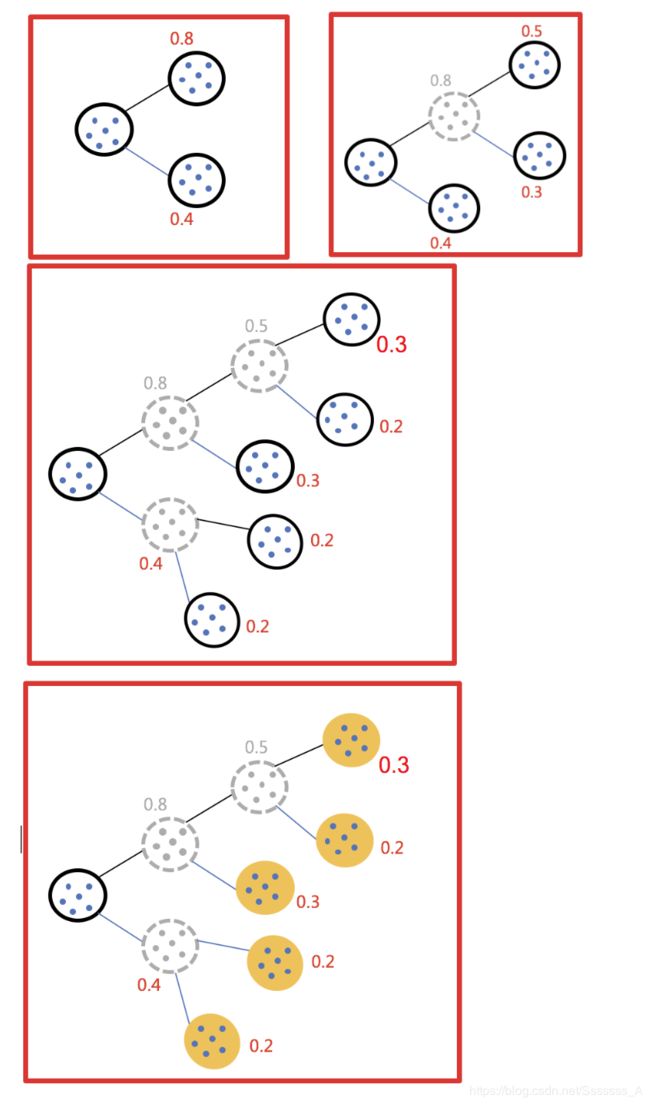
实现流程:
- 1.所有点作为一个簇
- 2.将该簇一分为二
- 3.选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。
- 4.以此进行下去,直到簇的数目等于用户给定的数目k为止。
隐含的一个原则
因为聚类的误差平方和能够衡量聚类性能,该值越小表示数据点越接近于他们的质心,聚类效果就越好。所以需要对误差平方和最大的簇进行再一次划分,因为误差平方和越大,表示该簇聚类效果越不好,越有可能是多个簇被当成了一个簇,所以我们首先需要对这个簇进行划分。
二分K均值算法可以加速K-means算法的执行速度,因为它的相似度计算少了并且不受初始化问题的影响,因为这里不存在随机点的选取,且每一步都保证了误差最小
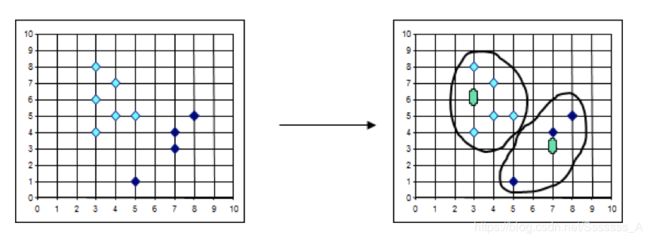
5.4 k-medoids(k-中心聚类算法)
K-medoids和K-means是有区别的,不一样的地方在于中心点的选取
- K-means中,将中心点取为当前cluster中所有数据点的平均值,对异常点很敏感!
- K-medoids中,将从当前cluster 中选取到其他所有(当前cluster中的)点的距离之和最小的点作为中心点。
算法流程:
( 1 )总体n个样本点中任意选取k个点作为medoids
( 2 )按照与medoids最近的原则,将剩余的n-k个点分配到当前最佳的medoids代表的类中
( 3 )对于第i个类中除对应medoids点外的所有其他点,按顺序计算当其为新的medoids时,代价函数的值,遍历所有可能,选取代价函数最小时对应的点作为新的medoids
( 4 )重复2-3的过程,直到所有的medoids点不再发生变化或已达到设定的最大迭代次数
( 5 )产出最终确定的k个类
k-medoids对噪声鲁棒性好。
例:当一个cluster样本点只有少数几个,如(1,1)(1,2)(2,1)(1000,1000)。其中(1000,1000)是噪声。如果按照k-means质心大致会处在(1,1)(1000,1000)中间,这显然不是我们想要的。这时k-medoids就可以避免这种情况,他会在(1,1)(1,2)(2,1)(1000,1000)中选出一个样本点使cluster的绝对误差最小,计算可知一定会在前三个点中选取。
k-medoids只能对小样本起作用,样本大,速度就太慢了,当样本多的时候,少数几个噪音对k-means的质心影响也没有想象中的那么重,所以k-means的应用明显比k-medoids多。
5.5 Kernel k-means
kernel k-means实际上,就是将每个样本进行一个投射到高维空间的处理,然后再将处理后的数据使用普通的k-means算法思想进行聚类。
5.6 ISODATA
类别数目随着聚类过程而变化;
对类别数会进行合并,分裂,
“合并”:(当聚类结果某一类中样本数太少,或两个类间的距离太近时)
“分裂”(当聚类结果中某一类的类内方差太大,将该类进行分裂)
5.7 Mini Batch K-Means
适合大数据的聚类算法
大数据量是什么量级?通常当样本量大于1万做聚类时,就需要考虑选用Mini Batch K-Means算法。
Mini Batch KMeans使用了Mini Batch(分批处理)的方法对数据点之间的距离进行计算。
Mini Batch计算过程中不必使用所有的数据样本,而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本量少,所以会相应的减少运行时间,但另一方面抽样也必然会带来准确度的下降。
该算法的迭代步骤有两步:
(1)从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心
(2)更新质心
与Kmeans相比,数据的更新在每一个小的样本集上。对于每一个小批量,通过计算平均值得到更新质心,并把小批量里的数据分配给该质心,随着迭代次数的增加,这些质心的变化是逐渐减小的,直到质心稳定或者达到指定的迭代次数,停止计算。
5.8总结
| 优化方法 | 思路 |
|---|---|
| anopy + kmeans | Canopy粗聚类配合kmeans |
| kmeans++ | 距离越远越容易成为新的质心 |
| 二分k-means | 拆除SSE最大的簇 |
| k-medoids | 和kmeans选取中心点的方式不同 |
| kernel kmeans | 映射到高维空间 |
| ISODATA | 动态聚类 |
| Mini-batch K-Means | 大数据集分批聚类 |
六.特征降维
6.1降维
6.1.1定义
降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程
正是因为在进行训练的时候,我们都是使用特征进行学习。如果特征本身存在问题或者特征之间相关性较强,对于算法学习预测会影响较大
6.1.2降维的两种方式
- 特征选择
- 主成分分析(可以理解成一种特征提取的方式)
6.2特征选择
6.2.1定义
数据中包含冗余或无关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征。
6.2.2方法
-
Filter(过滤式)主要探究特征本身特点、特征与特征和目标值之间关联
- 方差选择法:低方差特征过滤
- 相关系数
-
Embedded (嵌入式):算法自动选择特征(特征与目标值之间的关联)
- 决策树:信息熵、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
6.2.3低方差特征过滤
删除低方差的一些特征,前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。
- 特征方差小:某个特征大多样本的值比较相近
- 特征方差大:某个特征很多样本的值都有差别
-
API
- sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
- 删除所有低方差特征
- Variance.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。
- sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
-
数据计算
我们对某些股票的指标特征之间进行一个筛选,除去’index,‘date’,'return’列不考虑**(这些类型不匹配,也不是所需要指标)**
一共这些特征
pe_ratio,pb_ratio,market_cap,return_on_asset_net_profit,du_return_on_equity,ev,earnings_per_share,revenue,total_expenseindex,pe_ratio,pb_ratio,market_cap,return_on_asset_net_profit,du_return_on_equity,ev,earnings_per_share,revenue,total_expense,date,return 0,000001.XSHE,5.9572,1.1818,85252550922.0,0.8008,14.9403,1211444855670.0,2.01,20701401000.0,10882540000.0,2012-01-31,0.027657228229937388 1,000002.XSHE,7.0289,1.588,84113358168.0,1.6463,7.8656,300252061695.0,0.326,29308369223.2,23783476901.2,2012-01-31,0.08235182370820669 2,000008.XSHE,-262.7461,7.0003,517045520.0,-0.5678,-0.5943,770517752.56,-0.006,11679829.03,12030080.04,2012-01-31,0.09978900335112327 3,000060.XSHE,16.476,3.7146,19680455995.0,5.6036,14.617,28009159184.6,0.35,9189386877.65,7935542726.05,2012-01-31,0.12159482758620697 4,000069.XSHE,12.5878,2.5616,41727214853.0,2.8729,10.9097,81247380359.0,0.271,8951453490.28,7091397989.13,2012-01-31,-0.0026808154146886697分析:
1.初始化VarianceThreshold,指定阀值方差
2.调用fit_transform
def variance_demo(): """ 删除低方差特征——特征选择 :return: None """ data = pd.read_csv("factor_returns.csv") print(data) # 1、实例化一个转换器类 transfer = VarianceThreshold(threshold=1) # 2、调用fit_transform data = transfer.fit_transform(data.iloc[:, 1:10]) print("删除低方差特征的结果:\n", data) print("形状:\n", data.shape) return None返回结果
index pe_ratio pb_ratio market_cap \ 0 000001.XSHE 5.9572 1.1818 8.525255e+10 1 000002.XSHE 7.0289 1.5880 8.411336e+10 ... ... ... ... ... 2316 601958.XSHG 52.5408 2.4646 3.287910e+10 2317 601989.XSHG 14.2203 1.4103 5.911086e+10 return_on_asset_net_profit du_return_on_equity ev \ 0 0.8008 14.9403 1.211445e+12 1 1.6463 7.8656 3.002521e+11 ... ... ... ... 2316 2.7444 2.9202 3.883803e+10 2317 2.0383 8.6179 2.020661e+11 earnings_per_share revenue total_expense date return 0 2.0100 2.070140e+10 1.088254e+10 2012-01-31 0.027657 1 0.3260 2.930837e+10 2.378348e+10 2012-01-31 0.082352 2 -0.0060 1.167983e+07 1.203008e+07 2012-01-31 0.099789 ... ... ... ... ... ... 2315 0.2200 1.789082e+10 1.749295e+10 2012-11-30 0.137134 2316 0.1210 6.465392e+09 6.009007e+09 2012-11-30 0.149167 2317 0.2470 4.509872e+10 4.132842e+10 2012-11-30 0.183629 [2318 rows x 12 columns] 删除低方差特征的结果: [[ 5.95720000e+00 1.18180000e+00 8.52525509e+10 ..., 1.21144486e+12 2.07014010e+10 1.08825400e+10] [ 7.02890000e+00 1.58800000e+00 8.41133582e+10 ..., 3.00252062e+11 2.93083692e+10 2.37834769e+10] [ -2.62746100e+02 7.00030000e+00 5.17045520e+08 ..., 7.70517753e+08 1.16798290e+07 1.20300800e+07] ..., [ 3.95523000e+01 4.00520000e+00 1.70243430e+10 ..., 2.42081699e+10 1.78908166e+10 1.74929478e+10] [ 5.25408000e+01 2.46460000e+00 3.28790988e+10 ..., 3.88380258e+10 6.46539204e+09 6.00900728e+09] [ 1.42203000e+01 1.41030000e+00 5.91108572e+10 ..., 2.02066110e+11 4.50987171e+10 4.13284212e+10]] 形状: (2318, 8)
6.2.4相关系数
- 主要实现方式:
- 皮尔逊相关系数
- 斯皮尔曼相关系数
皮尔逊相关系数:
-
作用
反映变量之间相关关系密切程度的统计指标
-
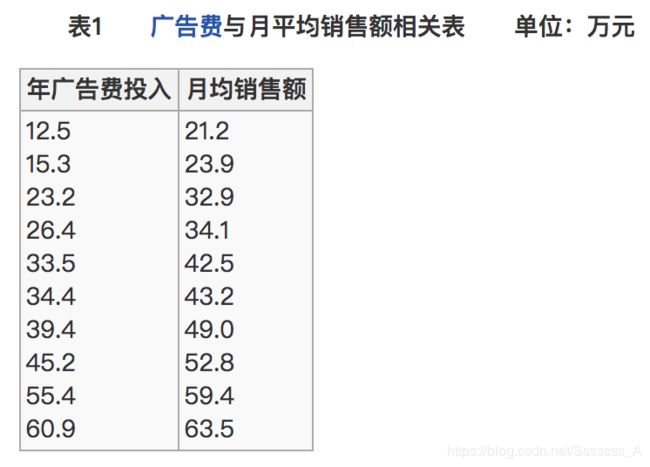
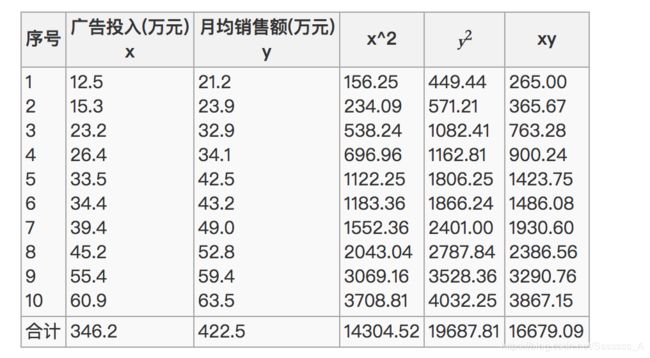
公式计算案例
公式:
举例:
-
特点
相关系数的值介于–1与+1之间,即–1≤ r ≤+1。其性质如下:
- 当r>0时,表示两变量正相关,r<0时,两变量为负相关
- 当|r|=1时,表示两变量为完全相关,当r=0时,表示两变量间无相关关系
- 当0<|r|<1时,表示两变量存在一定程度的相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
- 一般可按三级划分:|r|<0.4为低度相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关
-
api
- from scipy.stats import pearsonr
- x : (N,) array_like
- y : (N,) array_like Returns: (Pearson’s correlation coefficient, p-value)
- from scipy.stats import pearsonr
-
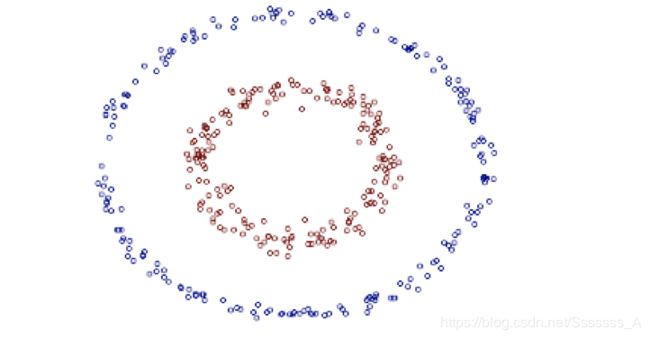
案例
from scipy.stats import pearsonr x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9] x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5] pearsonr(x1, x2)结果
(0.9941983762371883, 4.9220899554573455e-09)
斯皮尔曼相关系数
-
作用
反映变量之间相关关系密切程度的统计指标
-
公式计算案例
公式:
n为等级个数,d为二列成对变量的等级差数
举例:
-
特点
- 斯皮尔曼相关系数表明 X (自变量) 和 Y (因变量)的相关方向。 如果当X增加时, Y 趋向于增加, 斯皮尔曼相关系数则为正
- 与之前的皮尔逊相关系数大小性质一样,取值 [-1, 1]之间
斯皮尔曼相关系数比皮尔逊相关系数应用更加广泛
-
api
- from scipy.stats import spearmanr
-
案例
from scipy.stats import spearmanr x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9] x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5] spearmanr(x1, x2)结果:
SpearmanrResult(correlation=0.9999999999999999, pvalue=6.646897422032013e-64)
6.3主成分分析
6.3.1什么是主成分分析(PCA)
- 定义:高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量
- 作用:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
- 应用:回归分析或者聚类分析当中
对于信息一词,在决策树中会进行介绍
6.3.2 API
- sklearn.decomposition.PCA(n_components=None)
- 将数据分解为较低维数空间
- n_components:
- 小数:表示保留百分之多少的信息
- 整数:减少到多少特征
- PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后指定维度的array
6.3.3数据计算
先拿个简单的数据计算一下
[[2,8,4,5],
[6,3,0,8],
[5,4,9,1]]
from sklearn.decomposition import PCA
def pca_demo():
"""
对数据进行PCA降维
:return: None
"""
data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]
# 1、实例化PCA, 小数——保留多少信息
transfer = PCA(n_components=0.9)
# 2、调用fit_transform
data1 = transfer.fit_transform(data)
print("保留90%的信息,降维结果为:\n", data1)
# 1、实例化PCA, 整数——指定降维到的维数
transfer2 = PCA(n_components=3)
# 2、调用fit_transform
data2 = transfer2.fit_transform(data)
print("降维到3维的结果:\n", data2)
return None
返回结果:
保留90%的信息,降维结果为:
[[ -3.13587302e-16 3.82970843e+00]
[ -5.74456265e+00 -1.91485422e+00]
[ 5.74456265e+00 -1.91485422e+00]]
降维到3维的结果:
[[ -3.13587302e-16 3.82970843e+00 4.59544715e-16]
[ -5.74456265e+00 -1.91485422e+00 4.59544715e-16]
[ 5.74456265e+00 -1.91485422e+00 4.59544715e-16]]
七.案例:探究用户对物品类别的喜好细分降维
数据如下:
- order_products__prior.csv:订单与商品信息
- 字段:order_id, product_id, add_to_cart_order, reordered
- products.csv:商品信息
- 字段:product_id, product_name, aisle_id, department_id
- orders.csv:用户的订单信息
- 字段:order_id,user_id, eval_set,order_number,….
- aisles.csv:商品所属具体物品类别
- 字段: aisle_id, aisle
7.1需求
7.2分析
- 1.获取数据
- 2.数据基本处理
- 2.1 合并表格
- 2.2 交叉表合并
- 2.3 数据截取
- 3.特征工程 — pca
- 4.机器学习(k-means)
- 5.模型评估
- sklearn.metrics.silhouette_score(X, labels)
- 计算所有样本的平均轮廓系数
- X:特征值
- labels:被聚类标记的目标值
- sklearn.metrics.silhouette_score(X, labels)
7.3完整代码
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
-
获取数据
order_product = pd.read_csv("./data/instacart/order_products__prior.csv") products = pd.read_csv("./data/instacart/products.csv") orders = pd.read_csv("./data/instacart/orders.csv") aisles = pd.read_csv("./data/instacart/aisles.csv") -
数据基本处理
-
合并表格
table1 = pd.merge(order_product, products, on=["product_id", "product_id"]) table2 = pd.merge(table1, orders, on=["order_id", "order_id"]) table = pd.merge(table2, aisles, on=["aisle_id", "aisle_id"]) -
交叉表和并
table = pd.crosstab(table["user_id"], table["aisle"]) -
数据截取
table = table[:1000]
-
-
特征工程–PCA
transfer = PCA(n_components=0.9) data = transfer.fit_transform(table) -
机器学习–k-means
estimator = KMeans(n_clusters=8, random_state=22) estimator.fit_predict(data) -
模型评估
silhouette_score(data, y_predict)
八.算法选择
关于在计算的过程中,如何选择合适的算法进行计算,可以参考scikit learn官方给的指导意见