搜索与回溯算法
搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术来求解。
回溯是搜索算法中的一种控制策略。
回溯的基本思想是:为了求得问题的解,先选择某一种可能的情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或 证明无解
如迷宫问题:进入迷宫后,先随意选择一个前进方向,一步步向前试探前进,如果碰到死胡同,说明前进方向已无路可走,这时,首先看其他方向是否还有路可走,如果有路可走,则沿该方向在向前试探;如果无路可走,则返回一步,在看其他方向是否还有路可走;如果有路可走,则沿该方向再向前试探。按此原则不断搜索回溯在搜索,直到找到新的出路或原路返回入口处无解为止。
要有多个情况的才需要回溯
递归回溯算法框架【一】 我更喜欢这种,因为符合递归的思想书写形式
int search(int k)
{
if(到达目的) 输出解;
else
{
for(int i=1;i<=算符种数;i++)
{
if(满足条件)
{
保存结果;
search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
}
}递归回溯算法框架【二】
int search(int k)
{
for(int i=1;i<=算符种数;i++)
{
if(满足条件)
{
保存结果;
if(到达目的) 输出解;
else
search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
}例题1:素数环:从1到20这20个数摆成一个环,要求相邻的俩个数的和是一个素数。
算法分析:
非常明显这是一到回溯的题目。从1开始,每个空位有20个可能,只要填进去数合法,与前面的数不相同,与左边相邻的数和是一个素数。第二十个数还要和判断和第一个数的和是否是素数
其实这个和全排列差不多 就是加点东西而已
这个是我比较喜欢的框架为啥和下面那个x==n,但是这个是x=n+1,是因为这里的num还没有赋值来所以得到下一次去判断
这里的x就是控制每一层的数,反正再怎么递归它也不会超过我们给出的递归出口 比如x=n+1;
再者就是这个x也控制了数组num的每一个值了,再然后与上一相加是mun[x-1]因为x代表的是递归代表的层数,所以x-1肯定是
上一层,也就是上一个数组num的值了
可以看一下全排列和这个一起理解一下:全排列
#include
#include
#include
int n;
int num[10001]; //存储数据
bool mark[10001]; //判断该数是否被标记过
bool check(int x,int y) //判断是否满足"素数环"条件
{
int k=2,i=x+y;
while(k<=sqrt(i)&&i%k!=0) k++;
if(k>sqrt(i)) return true;
return false;
}
void print() //输出函数
{
for(int i=1;i #include
using namespace std;
int n;
int num[10001]; //存储数据
bool mark[10001]; //判断该数是否被标记过
bool check(int x,int y) //判断是否满足"素数环"条件
{
int k=2,i=x+y;
while(k<=sqrt(i)&&i%k!=0) k++;
if(k>sqrt(i)) return true;
return false;
}
void print() //输出函数
{
for(int i=1;i
例题2:八皇后问题(很经典)
规定 i:代表第i行 j代表第j列那么
a[i]=j; 代表是第i行,第j列
肯定八行都要放皇后,那么就是判断皇后是否安全:即检查同一列,同一对角线是否已有皇后,(行列坐标之和或行列坐标之差相等) (a[i]!=a[j])&&(abs(i-j)!=abs(a[i]-a[i])) (i和j分别表示俩个皇后的行号)
#include
using namespace std;
int a[9];
int b[9]={0};
int c[16]={0};
int d[16]={0};
int sum=0;
void print()
{
sum++;
cout<<"sum="<
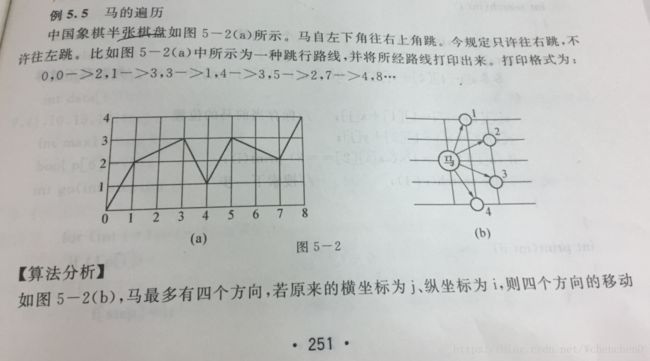
例题3:马的遍历
这个马的遍历只是往右上角从(0,0)跳到(4,8)因为每次在for循环里都会判断是否出了这个范围,而且只是一个方向,所以不需要回溯,因为他会一直往下跳,可以写但是执行结果是一样的
#include
using namespace std;
int a[100][3],t=0;//路径和路径总数
int x[4]={2,1,-1,-2};//四种移动规则
int y[4]={1,2,2,1};
void print(int n)
{
t++;
cout<<"t="<=0&&a[i-1][1]+x[j]<=4&&a[i-1][2]+y[j]>=0&&a[i-1][2]+y[j]<=8)
{
a[i][1]=a[i-1][1]+x[j];//保存当前马的位置
a[i][2]=a[i-1][2]+y[j];
if(a[i][1]==4&&a[i][2]==8) print(i);
else searchh(i+1);
}
}
}
int main()
{
a[1][1]=0;//从坐标(0,0)开始往右跳第二步
a[1][2]=0;
searchh(2);
}
例题4:
这题感觉还是很经典的
首先step是控制人的,每层递归都是A,B,C,D,E step都是他们其中的一个,所以在每层里用for控制工作j,然后就是递归遍历了,求出最大的解,其实知道最主要的思想其中的小细节去慢慢实现还是很容易的比如找到效益最高的一组输出,求最大值等等,然而这些都是是递归回溯法算法的框架中往里加的
#include
using namespace std;
int data[6][6]={{0,0,0,0,0,0},{0,13,11,10,4,7},{0,13,10,10,8,5},{0,5,9,7,7,4},{0,15,12,10,11,5},
{0,10,11,8,8,4}};
int maxn=0;
int g[10];//数组g存放最优的工作选择方案
int f[10];//用数组f储存搜索中工作选择的方案
bool p[6]={0}; //数组p用于表示某项工作有没有被选择了
int go(int step,int t)//step是第几个人,t是之前已得到的效益
{
for(int i=1;i<=5;i++)
{
if(!p[i])//判断第i项工作没人选择
{
f[step]=i;//第step个人,就选第i项工作
p[i]=1;//标记第i项工作被人安排了
t+=data[step][i];//计算效益值
if(step==5)
{
if(t>maxn)
{
maxn=t;
for(int j=1;j<=5;j++)
g[j]=f[j];//保存最优效益下的工作选择方案
}
}
else go(step+1,t);
t-=data[step][i];//回溯;
p[i]=0;
}
}
}
int main()
{
go(1,0);
for(int i=1;i<=5;i++)
{
cout<#include
using namespace std;
bool flag[6];
int sum=0;
int book[6];
bool like[6][6]={{0,0,0,0,0,0},{0,0,0,1,1,0},{0,1,1,0,0,1},{0,0,1,1,0,0},{0,0,0,0,1,0},{0,0,1,0,0,1}};
int print()
{
sum++;
cout<<"sum="<
例题6:跳马问题
这个问题和上一个马的问题还是有点区别的,因为这个是以坐标为二维数组的,上一个的目标就是求到达固定地坐标,而且还是有个问题是上一个没有判断这个啥啥是否被访问过,因为这个不需要,所以不用,但是大多数都是需要的
#include
using namespace std;
int u[8]={1,2,2,1,-1,-2,-2,-1};//八个方向上的x,y增量
int v[8]={-2,-1,1,2,2,1,-1,-2};
int a[100][100]={0};//a的值代表的是往下递归的第几层
int num=0;//代表的是方案数,跳遍真个棋盘要25步,所以用n代替层数,当能够跳够25 步时已经完成
bool b[100][100]={0};//这个相当于(x,y) 坐标,得判断坐标是否是合法,和这个坐标是否被访问过就是用b
void print()
{
num++;
if(num<=5)
{
for(int i=1;i<=5;i++)
{
for(int j=1;j<=5;j++)
{
cout<25)//达到最大规模打印,统计方案
{
print();
}
else
{
for(k=0;k<=7;k++)//遍历八个方向
{
x=i+u[k];//走此方向,得到的新坐标
y=j+v[k];
if(x<=5&&x>=1&&y<=5&&y>=1&&(!b[x][y]))//如果新坐标在棋盘上,并且这一格可以走
{
b[x][y]=1;
a[x][y]=n;
searchh(x,y,n+1);//从(x,y)去搜下一步该如何走
b[x][y]=0;
a[x][y]=0;
}
}
}
}
int main()
{
a[1][1]=1;//从(1,1)第一步开始走
b[1][1]=1;
searchh(1,1,2);
cout<