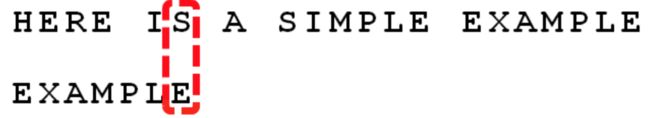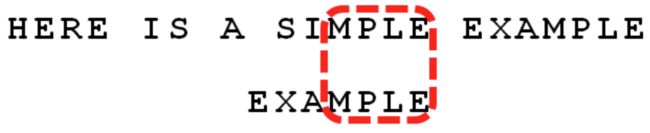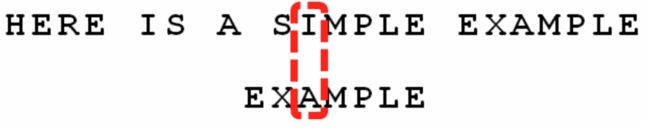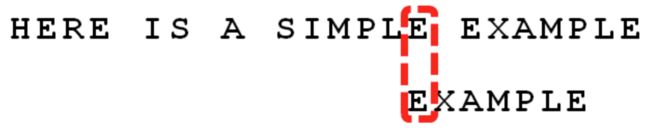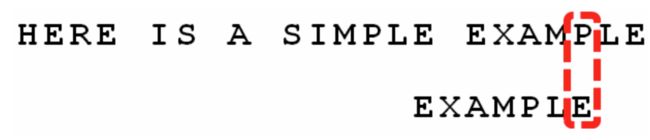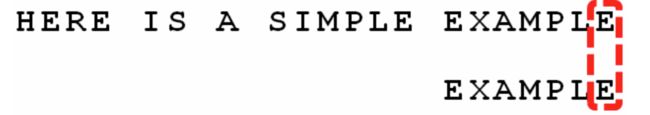BM算法

BM算法（Boyer-Moore算法）是由Robert S. Boyer和J Strother Moore于1997年发明的一种字符串匹配算法，该算法在实际实践中会比KMP算法效率高，因为BM算法即使在最坏情况下其时间复杂度也为O(N)，BM算法不仅算法效率高，而且构思非常巧妙，也很容易理解，下面我们来举例说明BM算法的运行过程：

匹配过程：

1）首先，字符串与搜索词头部对齐，从尾部字符开始比较：

这里跟KMP有很大的不同，就在于从尾部字符开始比较，这是一个非常巧妙的做法，很容易想到，如果对于尾部字符都不匹配的话，那么我们只要一次比较，就可以知道前面相应长度的字符必定不是期望的结果。

2）“S”与“E”不匹配，我们就将“S”称作“坏字符（bad character）”，即不匹配的字符，这时就可以将搜索词直接往后移动几位，这一过程被称作坏字符引起的模式滑动，那么具体应该移动多少位呢？这里存在一个移动规则叫做坏字符规则，规则如下：

step_bad = pos1 - pos2                        公式1

其中，step_bad表示向后移动位数；pos1表示坏字符的位置；pos2表示坏字符在搜索词中出现的最右位置

当然，有时也会出现坏字符不包含在搜索词中，那么这时pos2等于-1；

现在，我们来计算下面对上面的坏字符“S”，我们到底要往后移动多少位？

由于“S”对应的出现在搜索词的第6位（从0开始索引），所以pos1 = 6；

而由于“S”在搜索词中并未出现，所以pos2 = -1；

于是代入公式1可得：step_bad = 6-（-1）= 7；

于是移动7位变成如下：

3）同样的，依然从尾部开始比较，并且利用同样的移动规则，接下我们要移动6-4=2位，得到如下：

4）这时，出现了第一个匹配字符，同上依次比较和移动下去，会得到如下形式：

看到上图中，得到“MPLE”匹配字符串，我们把这个字符串成为“好后缀（good suffix）”，即所有尾部匹配的字符串；注意，“MPLE”，“PLE”，“LE”，“E”等都是好后缀；

关于好后缀，这里同样存在一个关于好后缀的规则：

step_good = pos1 - pos2                   公式2

其中，step_good为后移位数；pos1表示好后缀的位置；pos2表示好后缀在搜索词中剩余部分出现的最右位置；

当然，如果好后缀在搜索词中没有再次出现，设为-1；

5）再继续比较，变成下面：

上图中“I”与“A”不匹配，所以“I”是坏字符，根据坏字符规则，应该往后移动2-（-1）=3位，但是这里有一个容易忽略的重要问题，那就是3就是我们的最优移法么？答案是不一定，为什么？因为这时我们已经有了好后缀夹杂在里面，我们还需要考虑好后缀规则，这样结合得到的才是最优移法，那么根据好后缀规则有：

所有的好后缀：“MPLE”，“PLE”，“LE”，“E”，只有“E”在“EXAMPL”中出现，所以后移6-0=6位，这个值显然要比用坏字符规则求出的值要大，那我们到底是要移动3还是6呢？BM算法的做法是两者取最大者，即每次后移的位数，取两个规则中的较大者，所以我们应该往后移动6位：

这里要注意的是：不论是好后缀规则还是坏字符规则，他们的移动位数都只与搜索词（KMP中叫模式串）有关，而与原字符串（KMP中叫文本串）无关；

6）继续作尾部比较，有：

发现“P”和“E”不匹配，因此“P”是坏字符，根据坏字符规则，应该移动6-4=2位；这时不考虑好后缀规则，为什么呢，因为一开始从尾部字符就匹配失败，那么就还未得到好后缀，所以只考虑坏字符规则；

7）继续移动和比较，得到最终匹配结果：

好辣，至此我们就得到期望的匹配结果了，整个过程是不是很好理解很好懂呢，相信你已经看懂了。。