格子玻尔兹曼方法（LBM）的学习笔记1（附Couette流源代码及解析）

笔记目录

关于学习的教材及说明

在学习之前大致将流体力学学了一下包括一些概念的理解和重要的公式，在看这本《The Lattice Boltzmann Method Principles and Practice（2017）》之前已经看了郭照立老师的《格子Bolzmann方法的原理与应用》的前三章内容，由于基础差，感觉理解起来很吃力，于是转战这本英文教材，教材的前面是我已经看过的内容，所以从第二章开始学习，抱着看懂范例的目标，将部分内容略过，然后将自己觉得有意义的部分翻译成中文记录下来，部分翻译可能存在错误。此文算是比较正式的第一篇博文，希望能有所帮助。

外文教材的链接：链接：https://pan.baidu.com/s/1m–GxcGLPKK8_bgBGFlrTQ 提取码：r5q3

1.Chapter2 流体的数值求解方法介绍

主要讲解不同的方法，通过对比展示LBM的优缺点

1.1 传统N-S求解

有限差分法（FD）：原理简单，可以用于简单问题；但对于复杂变量的问题计算会很复杂且误差大精度不高。

有限体积法（FVM）：与FD相比，在默认情况下时守恒的，能通过细化网格以适应复杂几何机构的不规则网格；但不规则网格本身就很复杂，高阶的FV方法尤其是三维及不规则网格不容易计算，因此精度难以提高。

有限元方法（FEM）：对非结构网格具有良好的数学处理能力，并能通过高阶基函数提高精度；但不是守恒的，且较前两种方法而言更加复杂。

总结：都是从流体的宏观角度出发，针对N-S方程的求解衍生出来的，最终目的都是直接求解方程。

1.2 粒子法求解

从微观及介观的角度出发，通过粒子代表流体中的原子、分子、分子团或者宏观流体的一部分。

分子动力学（MD）：使用Verlet算法，通过粒子过去和现在的位移算将来的位移。虽然粒子法可以用来计算一些的复杂的过程，但是由于一般流体中的微观粒子数过多，计算量太大。
$$x_i(t+\Delta t)=2x_i(t)-x_i(t-\Delta t)+\frac{f_i(t)}{m_i}\Delta t^2$$

晶格模式（LGM）：将流体的运动用碰撞与流动两条准则来描述。格子只有两种状态，利于描述碰撞，因此没有其它CFD方法中浮点运算所固有的舍入误差，可以进行大量的并行运算；但是这种模式在速度增大时会逐渐失控，因此在用FHP模式求解N-S方程时只适用于低马赫数流动，同时晶格法还因为统计噪声而饱受争议。
$$n_i\left(x+c_i\Delta t,t+\Delta t\right)=n_i(x,t)+{\Omega }_i(x,t)$$

耗散分子动力学（DPD）：与LBM相似，是相对较新的介观流体计算方法，通过质量为m的粒子代替分子团，粒子自身的自由度被整合，粒子间的受力由一对保守力、耗散力与随机力表示，并以此保证动量守恒与正确的流体动力学行为。适用于具有有限克努森数的中尺度复杂流体的流体动力学及多相流；但它包含的参数过多需要进行筛选。

$$f_i=f_i^{\mathrm{e}\mathrm{x}\mathrm{t}}+\sum _{j̸=i}{f}_{ij}=f^{\mathrm{e}\mathrm{x}\mathrm{t}}+\sum _{j̸=i}\left(f_{ij}^{\mathrm{C}}+f_{ij}^{\mathrm{D}}+f_{ij}^{\mathrm{R}}\right)$$

多粒子碰撞动力学（MPC）：在尽可能地粗粒化物理系统，同时仍然解决问题底层的基本特征，适用于流体动力学与热力学相结合的复杂问题。满足三条法则：流动与碰撞互换；质量、动量守恒且满足H-定理；各向异性离散化。优点是易于实现和使用，计算效率高，易于并行化；但由于其强大的人工压缩性，不适合Stokes流动及可压缩流体力学。在无滑移边界条件下比LBM更易控制。
$$x_i(t+\Delta t)=x_i(t)+c_i(t)\Delta t$$

直接蒙特卡洛法（DSMC）：是一种基于动力学理论的粒子方法，通过概率模型模拟粒子的碰撞得到流动解，是解决高努森数流问题的主要方法。该算法能很好的描述物理效应（甚至超过LBM方法），其计算结果由样本规模及平均化过程决定，因此可能存在统计误差，其与计算粒子数N的开方呈反比，而计算的成本与粒子数呈正比，因此在保证精度的情况下需要满足较高的计算机资源，目前其在稀薄气体流动的计算方面有最高的精度，随着计算机技术的不断发展，该算法有非常大的潜力。

光滑粒子动力学（SPH）：是一种利用周围相互作用的粒子来进行插值计算的无网格方法。其原理及其自适应分辨率使其在处理具有巨大密度变化的大无界域时具有很大的优势，同时也可以很好的处理爆炸及高速撞击等大变形问题，在求解中能很好的实现质量与动量守恒；但是它的计算精度低，并且在处理边界条件是会变得很复杂，且很难与流体的宏观描述联系起来
$$\lambda (x)=\sum _j\frac{m_j}{{\rho }_j}{\lambda }_{j}W\left(\left|x-x_j\right|,h_j\right)$$

1.3 总结

传统方法是纯数值求解方法，旨在求解流体力学方程，这几种方法都是将流体变量(如速度和压力)表示为域中各个点(节点)的值，通过逼近域来求解偏微分方程。不同之处在于节点值的解释不同。其中FD用正方形网格上的节点值近似整个域，FV用节点值表示节点周围小体积内的流体变量平均值，FE通过节点插值逼近整个域。这些方法在原理上都相对简单，但由于流体力学的复杂性让求解依然比较困难。虽然对传统方法的研究较多，但多数求解依然局限在二阶精度。

粒子法不在于直接求解流体力学方程，而是通过粒子表示原子、分子、分子团或宏观流体的一部分，从而在一定程度上反映出流体的宏观规律，但是粒子法有的不能直接反映宏观流体运动规律，同时存在准确度难以量化、以及噪声问题等等。

LBM方法避免了传统方法求解流体力学方程的复杂求解及低精度，通过介观的方法避免了粒子法存在的噪声问题，具有很强的物理基础：Boltzmann方程，可以很好的将微观粒子的动力学与宏观流体规律相结合，同时具有较好的精度，因此是在很好的弱可压缩N-S方程二阶精准求解方法。
$$\frac{\partial f}{\partial t}+{\xi }_{\beta }\frac{\partial f}{\partial x_{\beta }}+\frac{F_{\beta }}{\rho }\frac{\partial f}{\partial {\xi }_{\beta }}=\Omega (f)$$

LBM方法的优缺点：

优点：简单高效；能适应复杂几何外形及软物质；能良好适应多相流及多组分问题；低噪声；可以适应热效应；

缺点：需要较大的内存，对于静止流体计算效率不高，不适用于强压缩性及，不适合在逼真粘度下直接模拟声音的远距离传播

2.Chapter3 LBM

总结性阐述LBM的过程，主要介绍BGK碰撞算子为例，介绍包括原理及简单案例的编程。

2.1 晶格玻尔兹曼方程

方程中的基本量$f_i(x,t)$为离散速度分布函数，表示在位置x时间t时速度为$c_i$的粒子密度，质量密度及动量密度可以表示为：
$$\rho (x,t)=\sum _i{f}_i(x,t),\rho u(x,t)=\sum _i{c}_i{f}_i(x,t)$$
DdQq中d表示维度，q表示速度分量数，常用的有D1Q3、D2Q9、D3Q15、D3Q19、D3Q27，三维问题中常用D3Q19。在等温问题中有压力与密度间的关系：$p=c_{\mathrm{s}}^2\rho$，其中$c_s=\frac{1}{\sqrt{3}}\frac{\Delta x}{\Delta t}$为声速，根据Boltzmann方程：$$f_i\left(x+c_i\Delta t,t+\Delta t\right)=f_i(x,t)+{\Omega }_i(x,t)$$
BGK碰撞算子：${\Omega }_i(f)=-\frac{f_i-f_i^{\mathrm{e}\mathrm{q}}}{\tau }\Delta t$，其中平衡态分布函数可以表示为：$f_i^{\mathrm{e}\mathrm{q}}(x,t)=w_i\rho \left(1+\frac{u\cdot c_i}{c_{\mathrm{s}}^2}+\frac{{\left(u\cdot c_i\right)}^2}{2c_{\mathrm{s}}^4}-\frac{u\cdot u}{2c_{\mathrm{s}}^2}\right)$,$w_i$为速度分量$c_i$的权重值。运动粘度可以通过松弛时间表示为：$v=c_{\mathrm{s}}^2\left(\tau -\frac{\Delta t}{2}\right)$带BGK碰撞算子的全离散玻尔兹曼方程为：$f_i\left(x+c_i\Delta t,t+\Delta t\right)=f_i(x,t)-\frac{\Delta t}{\tau }\left(f_i(x,t)-f_i^{\mathrm{e}\mathrm{q}}(x,t)\right)$

，包括粒子的碰撞与扩散两个过程。

2.2 LBM的简单编程实现

基于BGK算子的LBM编程流程图如下所示。

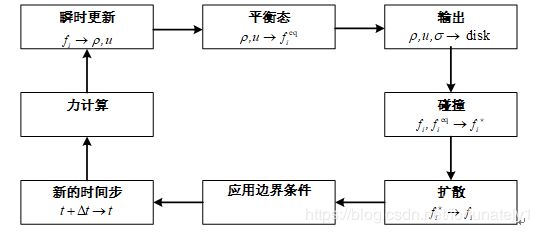
1.初始化：
$f_i^{\mathrm{e}\mathrm{q}}(x,t=0)=f_i^{\mathrm{e}\mathrm{q}}(\rho (x,t=0),u(x,t=0))$
$\rho (x,t=0)=1,u(x,t=0)=0$

2.时间步迭代算法：

a.通过公式先计算出：
$\rho (x,t)=\sum _i{f}_i(x,t),\rho u(x,t)=\sum _i{c}_i{f}_i(x,t)$
b.通过公式计算平衡态分布函数：
$f_i^{\mathrm{e}\mathrm{q}}(x,t)=w_i\rho \left(1+\frac{u\cdot c_i}{c_{\mathrm{s}}^2}+\frac{{\left(u\cdot c_i\right)}^2}{2c_{\mathrm{s}}^4}-\frac{u\cdot u}{2c_{\mathrm{s}}^2}\right)$
c.通过公式计算粘性应力张量：
${\sigma }_{\alpha \beta }\approx -\left(1-\frac{\Delta t}{2\tau }\right)\sum _i{c}_{i\alpha }{c}_{i\beta }(f_i-f_i^{\mathrm{e}\mathrm{q}})$
d.通过公式计算粒子碰撞后分布函数：
$f_i^{\ast }(x,t)=f_i(x,t)\left(1-\frac{\Delta t}{\tau }\right)+f_i^{\mathrm{e}\mathrm{q}}(x,t)\frac{\Delta t}{\tau }$
e.通过公式计算粒子扩散：
$f_i\left(x+c_i\Delta t,t+\Delta t\right)=f_i^{\star }(x,t)$

f.时间步增加，回到步骤a重复计算，当算到最后一步或者收敛时停止。
注：先算碰撞或者先算碰撞都可以。
（公式过多，懒得再弄一遍，直接弄成图片啦）

4 代码

clear all
close all
clc

% simulation parameters

scale=1;                % set simulation size
NX=3*scale;             % channel length  
NY=5*scale;             % channel width 
NSTEPS=1e4*scale^2;     % number of simulation time steps
tau=0.9;                % relaxation time (BGK model) 
omega=1/tau;
u_max=0.1/scale;        % maximum velocity 
nu=(2*tau-1)/6;         % kinematic shear viscosity  
Re=NY*u_max/nu;         % Reynolds number; scaling parameter in simulation 

% Lattice parameters; note zero direction is last 

NPOP=9;                                         % number of velocities
w = [1/9 1/9 1/9 1/9 1/36 1/36 1/36 1/36 4/9]; % weights  
cx = [1 0 -1  0 1 -1 -1  1 0];                  %velocities, x components 
cy = [0 1 0 -1 1  1 -1 -1 0];                  % velocities, y components

% Node locations 
x = (1:NX)-0.5;
y = (1:NY)-0.5;

% Analytical solution: Couette velocity 
u_analy=u_max/NY.*y; %沿Y向的速度分布
 
 % initialize populations 
feq=zeros(NX,NY,NPOP); %生成3*5*9的零矩阵
for k=1:NPOP
  
feq( : , : ,k)=w(k); % assuming density equal one and zero velocity initial state 
end
f=feq;
fprop=feq;
 
% convergence parameters 
tol=1e-12;      % tolerance to steady state convergence 
teval=100;      % time step to evaluate convergence 
u_old=zeros(NX,NY); 

% initalize clock
tstart = tic;

 % Main algorithm
for t=1:NSTEPS
    %Compute macroscopic quantities
    %density
   rho = sum(fprop,3); %密度

        %momentum components
    u= sum(fprop(:,:,[1 5 8]),3) - sum(fprop(:,:,[3 6 7]),3); %X向动量
    v =sum(fprop(:,:,[2 5 6]),3) - sum(fprop(:,:,[4 7 8]),3); %Y向动量
  
    % check convergence
   
if mod(t,teval)==1  %mod是取余函数即判断步数是否是100的步数+1
      conv = abs(mean(u(:))/mean(u_old(:))-1);  
            
if conv