AVL平衡树(详解)-JAVA/C版本
平衡二叉树在进行插入操作的时候可能出现不平衡的情况,AVL树即是一种自平衡的二叉树.
它通过旋转不平衡的节点来使二叉树重新保持平衡,并且查找、插入和删除操作在平均和最坏情况下时间复杂度都是O(log n)
AVL树的旋转一共有四种情形,注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。
RBT VS AVL:
实际上插入AVL树和红黑树的速度取决于你所插入的数据.如果你的数据分布较好,则比较宜于采用AVL树(例如随机产生系列数),
但是如果你想处理比较杂乱的情况,则红黑树是比较快的,因为红黑树对已经处理好的数据重新平衡减少了不心要的操作.另外一方面,如果是一种非寻常的插入系列比较常见(比如,插入密钥系列),则AVL树比较快,因为它的严格的平衡规则将会减少树的高度
在做插入和删除操作的时候,AVL树要做的调整比红黑树多了很多
RBT调整到平衡最多只需旋转2次,这就是优点,高度不会超过2lg(n),所以查找效率一样
老式的Linux内核的任务调度就是用的AVL,从某一个版本开始换RBT了.
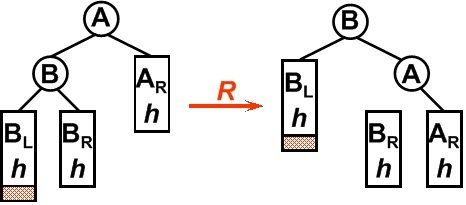
1. LL型
平衡二叉树某一节点的左孩子的左子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向右旋转一次即可,如图所示,原A的左孩子B变为父结点,A变为其右孩子,而原B的右子树变为A的左子树,注意旋转之后Brh是A的左子树(图上忘在A于Brh之间标实线)
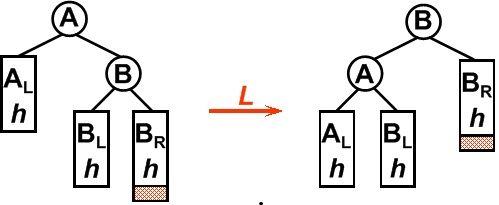
2. RR型
平衡二叉树某一节点的右孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向左旋转一次即可,如图所示,原A右孩子B变为父结点,A变为其左孩子,而原B的左子树Blh将变为A的右子树。
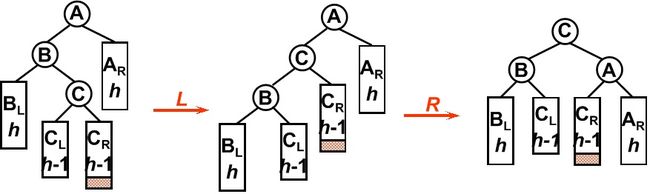
3. LR型
平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,这时还需要再向右旋转一次。
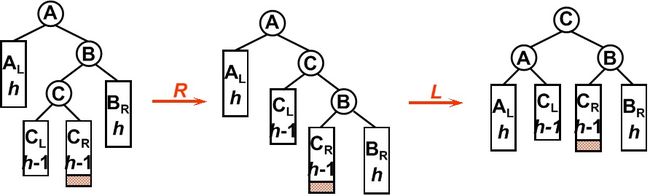
4. RL型
平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。
import java.util.Arrays;
import java.util.Collection;
import java.util.Scanner;
public class Main {
static Node proot = null;
static int TOT = 0;
/**
* 中序遍历打印AVL树
* @param node
*/
static void print(Node node) {
if (null == node)
return;
print(node.lson);
System.out.print(node.data + "("+node.freq +") ");
print(node.rson);
}
/**
* 求树的高度
* @param node
* @return
*/
static int getHigh(Node node) {
if (null == node)
return -1;
return node.high;
}
/**
* AVL查找
* @param node
* @param data
* @return
*/
static Node find(Node node, int data) {
if (null == node)
return null;
if (node.data < data)
return find(node.lson, data);
else if (node.data > data)
return find(node.rson, data);
else
return node;
}
/**
* AVL插入
* @param node
* @param data
* @return
*/
static Node insert(Node node, int data) {
if (null == node){
node = new Node(data);
TOT++;
} else if (node.data > data) {
node.lson = insert(node.lson, data);
if (getHigh(node.lson) - getHigh(node.rson) == 2) {
if (data < node.lson.data)
node = LL(node);
else
node = DL(node);
}
} else if (data > node.data) {
node.rson = insert(node.rson, data);
if (getHigh(node.rson) - getHigh(node.lson) == 2) {
if (data > node.rson.data)
node = RR(node);
else
node = DR(node);
}
} else
node.freq++;
node.high = Math.max(getHigh(node.lson), getHigh(node.rson)) + 1;
return node;
}
/**
* AVL单左旋转
* @param node
* @return
*/
static Node LL(Node node) {
Node t = node.lson;
node.lson = t.rson;
t.rson = node;
node.high = Math.max(getHigh(node.rson), getHigh(node.lson)) + 1;
t.high = Math.max(getHigh(t.rson), t.high) + 1;
return t;
}
/**
* AVL单右旋转
* @param node
* @return
*/
static Node RR(Node node) {
Node t = node.rson;
node.rson = t.lson;
t.lson = node;
node.high = Math.max(getHigh(node.rson), getHigh(node.lson)) + 1;
t.high = Math.max(getHigh(t.rson), t.high) + 1;
return t;
}
/**
* AVL双左旋转,即先右在左
* @param node
* @return
*/
static Node DL(Node node) {
node.lson = RR(node.lson);
return LL(node);
}
/**
* AVL双右旋转,即先左再右
* @param node
* @return
*/
static Node DR(Node node) {
node.rson = LL(node.rson);
return RR(node);
}
/**
* AVL删除
* @param node
* @param data
* @return
*/
static Node delete(Node node, int data) {
if (null == node)
;
else if (data < node.data) {
node.lson = delete(node.lson, data);
if (2 == getHigh(node.rson) - getHigh(node.lson)) {
if (getHigh(node.rson.lson) > getHigh(node.rson.rson))
node = DR(node);
else
node = RR(node);
}//在左边删一个点,右边的height有可能更大了
} else if (data > node.data) {
node.rson = delete(node.rson, data);
if (2 == getHigh(node.lson) - getHigh(node.rson)) {
if (getHigh(node.lson.rson) > getHigh(node.lson.lson))
node = DL(node);
else
node = LL(node);
}//在右边删一个点,左边的height有可能更大了
} else{
if(null == node.lson && null == node.rson){
node = null;//刚开始这里漏了
}else if(null != node.lson && null != node.rson){
Node now = node.rson;
while(null != now.lson )
now = now.lson;//找到要删除点右子树的最左树
node.data = now.data;
node.freq = now.freq;
node.rson = delete(node.rson,node.data);
if (2 == getHigh(node.lson) - getHigh(node.rson)) {
if (getHigh(node.lson.rson) > getHigh(node.lson.lson))
node = DL(node);
else
node = LL(node);
}
}else{
if(null == node.lson)
node = node.rson;
else node = node.lson;
}
}
if(null == node) return null;
node.high = Math.max(getHigh(node.lson), getHigh(node.rson)) + 1;
return node;
}
/**
* 更新操作,先删除再插入
* @param node
* @param data
* @param newdata
* @return
*/
static Node update(Node node, int data, int newdata) {
node = delete(node,data);
return insert(node,newdata);
}
/**
* 后序遍历删除树
* @param node
*/
static void deleteTree(Node node){
if(null == node)
return;
deleteTree(node.lson);
deleteTree(node.rson);
node.free();
}
public static void main(String[] args) {
System.out.println("AVL Tree");
int [] num = new int [20];
Node root = null;
for (int i = 0; i < 20; i++) {
num[i] = (int) (Math.random() * 1000);
root = insert(root, num[i]);
}
print(root);
System.out.printf("\n");
root = update(root,num[3],(int) (Math.random() * 1000));
root = update(root,num[5],(int) (Math.random() * 1000));
root = update(root,num[9],(int) (Math.random() * 1000));
print(root);
System.out.printf("\n");
root = delete(root,num[1]);
root = delete(root,num[2]);
root = delete(root,num[7]);
print(root);
System.out.printf("\n");
}
}
class Node {
Node lson, rson;
int high;
int data;
int freq;
public Node() {
super();
lson = rson = null;
freq = high = 0;
}
public Node(int data) {
// TODO Auto-generated constructor stub
this();
this.data = data;
}
public void free(){
this.lson = this.rson = null;
}
}C:
#include
#include
#include
typedef struct AVLTree
{
int nData;
struct AVLTree* pLeft;
struct AVLTree* pRight;
int nHeight;
}AVLTree;
int Max(int a, int b);
int Height(AVLTree* pNode);
AVLTree* Insert(int nData, AVLTree* pNode);
AVLTree* SingleRotateWithLeft(AVLTree* pNode);
AVLTree* SingleRotateWithRight(AVLTree* pNode);
AVLTree* DoubleRotateWithLeft(AVLTree* pNode);
AVLTree* DoubleRotateWithRight(AVLTree* pNode);
void DeleteTree(AVLTree** ppRoot);
void PrintTree(AVLTree* pRoot);
int main()
{
int i;
AVLTree* pRoot = NULL;
srand((unsigned int)::time(NULL));
for (i = 0; i < 10000; ++i)
{
pRoot = Insert(::rand(), pRoot);
}
PrintTree(pRoot);
DeleteTree(&pRoot);
return 0;
}
int Max(int a, int b)
{
return (a > b ? a : b);
}
int Height(AVLTree* pNode)
{
if (NULL == pNode)
return -1;
return pNode->nHeight;
}
AVLTree* Insert(int nData, AVLTree* pNode)
{
if (NULL == pNode)
{
pNode = (AVLTree*)malloc(sizeof(AVLTree));
pNode->nData = nData;
pNode->nHeight = 0;
pNode->pLeft = pNode->pRight = NULL;
}
else if (nData < pNode->nData) /// 插入到左子树中
{
pNode->pLeft = Insert(nData, pNode->pLeft);
if (Height(pNode->pLeft) - Height(pNode->pRight) == 2) /// AVL树不平衡
{
if (nData < pNode->pLeft->nData)
{
/// 插入到了左子树左边, 做单旋转
pNode = SingleRotateWithLeft(pNode);
}
else
{
/// 插入到了左子树右边, 做双旋转
pNode = DoubleRotateWithLeft(pNode);
}
}
}
else if (nData > pNode->nData) /// 插入到右子树中
{
pNode->pRight = Insert(nData, pNode->pRight);
if (Height(pNode->pRight) - Height(pNode->pLeft) == 2) /// AVL树不平衡
{
if (nData > pNode->pRight->nData)
{
/// 插入到了右子树右边, 做单旋转
pNode = SingleRotateWithRight(pNode);
}
else
{
/// 插入到了右子树左边, 做双旋转
pNode = DoubleRotateWithRight(pNode);
}
}
}
pNode->nHeight = Max(Height(pNode->pLeft), Height(pNode->pRight)) + 1;
return pNode;
}
/********************************************************************
pNode pNode->pLeft
/ \
pNode->pLeft ==> pNode
\ /
pNode->pLeft->pRight pNode->pLeft->pRight
*********************************************************************/
AVLTree* SingleRotateWithLeft(AVLTree* pNode)
{
AVLTree* pNode1;
pNode1 = pNode->pLeft;
pNode->pLeft = pNode1->pRight;
pNode1->pRight = pNode;
/// 结点的位置变了, 要更新结点的高度值
pNode->nHeight = Max(Height(pNode->pLeft), Height(pNode->pRight)) + 1;
pNode1->nHeight = Max(Height(pNode1->pLeft), pNode->nHeight) + 1;
return pNode1;
}
/********************************************************************
pNode pNode->pRight
\ /
pNode->pRight ==> pNode
/ \
pNode->pRight->pLeft pNode->pRight->pLeft
*********************************************************************/
AVLTree* SingleRotateWithRight(AVLTree* pNode)
{
AVLTree* pNode1;
pNode1 = pNode->pRight;
pNode->pRight = pNode1->pLeft;
pNode1->pLeft = pNode;
/// 结点的位置变了, 要更新结点的高度值
pNode->nHeight = Max(Height(pNode->pLeft), Height(pNode->pRight)) + 1;
pNode1->nHeight = Max(Height(pNode1->pRight), pNode->nHeight) + 1;
return pNode1;
}
AVLTree* DoubleRotateWithLeft(AVLTree* pNode)
{
pNode->pLeft = SingleRotateWithRight(pNode->pLeft);
return SingleRotateWithLeft(pNode);
}
AVLTree* DoubleRotateWithRight(AVLTree* pNode)
{
pNode->pRight = SingleRotateWithLeft(pNode->pRight);
return SingleRotateWithRight(pNode);
}
/// 后序遍历树以删除树
void DeleteTree(AVLTree** ppRoot)
{
if (NULL == ppRoot || NULL == *ppRoot)
return;
DeleteTree(&((*ppRoot)->pLeft));
DeleteTree(&((*ppRoot)->pRight));
free(*ppRoot);
*ppRoot = NULL;
}
/// 中序遍历打印树的所有结点, 因为左结点 < 父结点 < 右结点, 因此打印出来数据的大小是递增的
void PrintTree(AVLTree* pRoot)
{
if (NULL == pRoot)
return;
static int n = 0;
PrintTree(pRoot->pLeft);
printf("[%d]nData = %d\n", ++n, pRoot->nData);
PrintTree(pRoot->pRight);
}