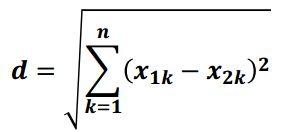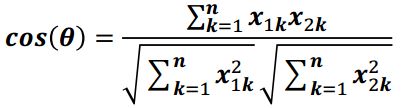python3（五）无监督学习

无监督学习

目录

• 1 关于机器学习
• 2 sklearn库中的标准数据集及基本功能
  • 2.1 标准数据集
  • 2.2 sklearn库的基本功能
• 3 关于无监督学习
• 4 K-means方法及应用
• 5 DBSCAN方法及应用
• 6  PCA方法及其应用
• 7 NMF方法及其实例
• 8 基于聚类的“图像分割”

 

正文

回到顶部

1 关于机器学习

　　机器学习是实现人工智能的手段, 其主要研究内容是如何利用数据或经验进行学习, 改善具体算法的性能 

　　　　多领域交叉, 涉及概率论、统计学, 算法复杂度理论等多门学科

　　　　广泛应用于网络搜索、垃圾邮件过滤、推荐系统、广告投放、信用评价、欺诈检测、股票交易和医疗诊断等应用
　　机器学习的分类

　　　　监督学习 （Supervised Learning）

　　　　　　从给定的数据集中学习出一个函数, 当新的数据到来时, 可以根据这个函数预测结果, 训练集通常由人工标注

　　　　无监督学习 （Unsupervised Learning）

　　　　　　相较于监督学习, 没有人工标注

　　　　强化学习（Reinforcement Learning，增强学习）

　　　　　　通过观察通过什么样的动作获得最好的回报, 每个动作都会对环境有所影响, 学习对象通过观察周围的环境进行判断

　　　　半监督学习（Semi-supervised Learning）

　　　　　　介于监督学习和无监督学习

　　　　深度学习 (Deep Learning)

　　　　　　利用深层网络神经模型, 抽象数据表示特征

　　在Python中使用Scikit-learn(简化为sklearn)这一模块来处理机器学习

　　　　官网

　　　　主要是依赖于numpy, scipy和matplotlib库

　　　　开源可复用

　　sklearn中机器学习模型十分丰富, 需要根据问题的类型来选择适当的模型

　　sklearn常用的函数

　　

　　关于sklearn库

　　　　sklearn是scikit-learn的简称，是一个基于Python的第三方模块。sklearn库集成了一些常用的机器学习方法，在进行机器学习任务时，并不需要实现算法，只需要简单的调用sklearn库中提供的模块就能完成大多数的机器学习任务。

　　　　安装sklearn库需要安装numpy, scipy(sklearn的基础, 集成了多种数学算法和函数), matplotlib(数据绘图工具)

　　　　安装地址

　　　　注意安装有顺序: numpy -> scipy -> matplotlib -> sklearn

回到顶部

2 sklearn库中的标准数据集及基本功能

2.1 标准数据集

　　

　　1) 波士顿房价数据集

　　　　波士顿房价数据集包含506组数据，每条数据包含房屋以及房屋周围的详细信息。其中包括城镇犯罪率、一氧化氮浓度、住宅平均房间数、到中心区域的加距离以及自住房平均房价等。因此，波士顿房价数据集能够应用到回归问题上。

　　　　加载数据集

sklearn.datasets.load_boston()

　　　　其中有参数return_X_y, 设置为True是会返回(data, target)两个数据, 默认为False, 只返回data(包含了data和target两个部分的内容)

　　　　具体使用

　　　　

　　2) 鸢尾花数据集

　　　　鸢尾花数据集采集的是鸢尾花的测量数据以及其所属的类别

　　　　测量数据包括: 萼片长度、萼片宽度、花瓣长度、花瓣宽度

　　　　类别共分为三类: Iris Setosa，Iris Versicolour，Iris Virginica, 该数据集可用于多分类问题

　　　　加载数据集

sklearn.datasets. load_iris()

　　　　同样有参数return_X_y, 使用方法雷同

　　　　具体实例

　　　　

　　3) 手写数字数据集

　　　　手写数字数据集包括1797个0-9的手写数字数据，每个数字由8*8大小的矩阵构成，矩阵中值的范围是0-16，代表颜色的深度。

　　　　加载数据集

sklearn.datasets.load_digits()

　　　　return_X_y: 效果依旧, True返回(data, target), 默认False直接返回全部内容

　　　　n_class: 设置数据类别, 返回数据的类别比设置类别低的数据样本, 设置为5就会返回0~4的数据 

　　　　基本使用
　　　　

2.2 sklearn库的基本功能

　　sklearn库的共分为6大部分，分别用于完成分类任务、回归任务、聚类任务、降维任务、 模型选择以及数据的预处理

　　1) 分类任务

　　

　　2) 回归任务

　　

　　3) 聚类任务

 　　

　　4) 降维任务

　　

回到顶部

3 关于无监督学习

　　无监督学习的目标

　　　　利用无标签的数据学习数据的分布或数据与数据之间的关系被称作无监督学习

　　　　有监督学习和无监督学习的最大区别在于数据是否有标签

　　　　无监督学习最常应用的场景是聚类(clustering)和降维(DimensionReduction)

　　聚类

　　　　聚类(clustering)，就是根据数据的“相似性”将数据分为多类的过程

　　　　评估两个不同样本之间的“相似性” ，通常使用的方法就是计算两个样本之间的“距离”。使用不同的方法计算样本间的距离会关系到聚类结果的好坏

　　1) 欧氏距离

　　　　欧氏距离是最常用的一种距离度量方法，源于欧式空间中两点的距离。

　　　　计算公式

　　　　

　　　　直观表示

　　　　

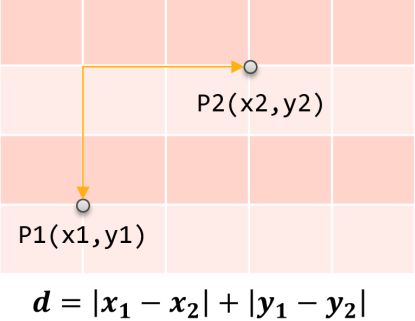
　　2) 曼哈顿距离

　　　　曼哈顿距离也称作“城市街区距离”，类似于在城市之中驾车行驶，从一个十字路口到另外一个十字楼口的距离(x与y两个方向的距离之和)

　　　　计算公式

 　　　　

　　　　直观表示

　　　　

　　3) 马氏距离

　　　　马氏距离表示数据的协方差距离，是一种尺度无关的度量方式。也就是说马氏距离会先将样本点的各个属性标准化，再计算样本间的距离。

　　　　计算公式, 其中s是协方差矩阵

　　　　

　　　　马氏空间的距离

　　　　

　　4) 夹角余弦

　　　　余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。余弦值越接近1，说明两个向量夹角越接近0度，表明两个向量越相似

　　　　计算公式

　　　　

　　　　二维空间显示

　　　　

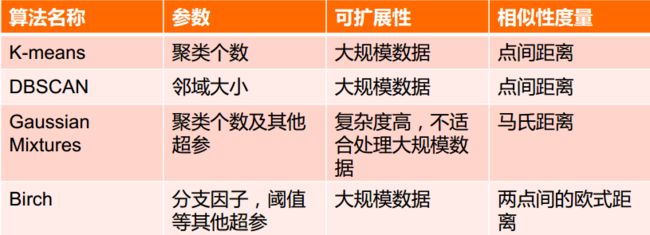
　　sklearn提供的常用聚类算法函数包含在sklearn.cluster这个模块中

　　以同样的数据集应用于不同的算法，可能会得到不同的结果，算法所耗费的时间也不尽相同，这是由算法的特性决定的

　　sklearn.cluster

　　　　sklearn.cluster模块提供的各聚类算法函数可以使用不同的数据形式作为输入

　　　　标准数据输入格式:[样本个数，特征个数]定义的矩阵形式

　　　　相似性矩阵输入格式：即由[样本数目，样本数目]定义的矩阵形式，矩阵中的每一个元素为两个样本的相似度，如DBSCAN，AffinityPropagation(近邻传播算法)接受这种输入。如果以余弦相似度为例，则对角线元素全为1. 矩阵中每个元素的取值范围为[0,1]

　　具有代表性的聚类函数

　　　　

　　降维

　　　　降维就是在保证数据所具有的代表性特征或分布的情况下, 将高维数据转化为低维数据的过程

　　　　作用:

　　　　　　数据可视化

　　　　　　作为中间过程, 起到精简数据, 提高其他机器学习算法效率的作用

　　分类和降维

　　　　聚类和分类都是无监督学习的典型任务，任务之间存在关联，比如某些高纬数据的分类可以通过降维处理更好的获得，另外学界研究也表明代表性的分类算法如k-means与降维算法如NMF之间存在等价性

　　sklearn和降维

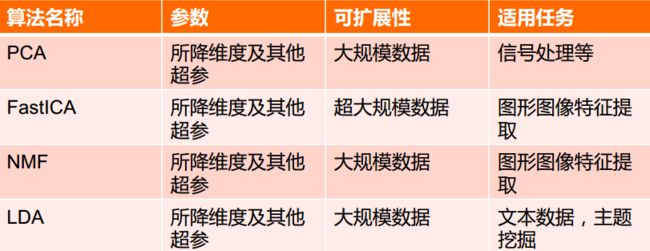
　　　　降维是机器学习领域的一个重要研究内容，有很多被工业界和学术界接受的典型算法，截止到目前sklearn库提供7种降维算法

　　　　降维过程也可以被理解为对数据集的组成成份进行分解（decomposition）的过程，因此sklearn为降维模块命名为decomposition, 在对降维算法调用需要使用sklearn.decomposition模块

　　　　sklearn.decomposition的常用算法

　　　　

回到顶部

4 K-means方法及应用

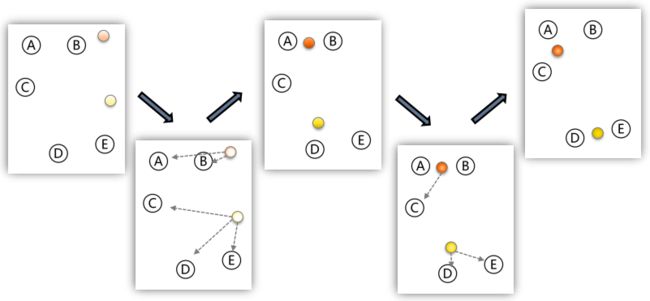
　　k-means算法也就是k均值算法

　　k-means算法以k为参数，把n个对象分成k个簇, 使簇内具有较高的相似度, 而簇间的相似度较低

　　处理结果如下

　　　　1 随机选择k个点作为初始的聚类中心；

　　　　2 对于剩下的点，根据其与聚类中心的距离，将其归入最近的簇

　　　　3 对每个簇，计算所有点的均值作为新的聚类中心

　　　　4 重复2、 3直到聚类中心不再发生改变

　　k-meams方法的处理过程如下

　　　　

　　创建k-means实例

　　　　创建实例

sklearn.cluster.Kmeans()

　　　　n_clusters: 用于指定聚类中心的个数, 一般设定此参数, 别的参数使用默认值

　　　　init: 初始聚类中心的初始化方法, 默认值是k-means++

　　　　max_iter: 最大的跌打次数, 默认值是30

　　创建实例后, 可以通过实例对象调用fit_predict()计算簇中心以及为簇分配序号

　　　　其中会传入参数data, 用于传入需要加载的数据

　　　　返回的结果是一个label, 是聚类后各个数据所属的标签

　　k-means实例还有一个参数 cluster_centers_, 可以通过处理该参数的值来得到更进一步的处理数据　　

　　k-means的应用

　　处理中国1999年各省份的消费水平

　　　　处理的技术路线: sklearn.cluster.Kmeans

　　　　数据模型为

　　　　

　　　　具体实例代码如下

import numpy as np
from sklearn.cluster import KMeans


def loadData(filePath):
    fr = open (filePath, 'r+' )
    lines = fr.readlines()
    retData = []
    retCityName = []
    for line in lines:
        items = line.strip().split( "," )
        retCityName.append(items[ 0 ])
        retData.append([ float (items[i]) for i in range ( 1 , len (items))])
    return retData,retCityName


if __name__ = = '__main__' :
    data,cityName = loadData( '31省市居民家庭消费水平-city.txt' )
    km = KMeans(n_clusters = 4 )
    label = km.fit_predict(data)
    expenses = np. sum (km.cluster_centers_,axis = 1 )
    #print(expenses)
    CityCluster = [[],[],[],[]]
    for i in range ( len (cityName)):
        CityCluster[label[i]].append(cityName[i])
    for i in range ( len (CityCluster)):
        print ( "Expenses:%.2f" % expenses[i])
        print (CityCluster[i])

　　　　程序结果

　　　　

　　深入程序解释

　　　　label是一个列表类型, 具体的值是 对应的数据被分成哪一类的索引

　　　　也就是说, 遍历cityname的时候同步取得label的值, 就可以对应的把城市名字放到合适的分类中, 这就是下面这句话的来源

CityCluster[label[i]].append(cityName[i])

　　　　生成的cluster_centers_是一个二维数据, 是一个列表里面套列表, 里面列表存储的是一个分类中, 每个城市的值对应处理得到的结果

　　　　所以对这个值在1维上相加得到的就是每一个聚类的综合的值, 这就是这句话的来源

expenses = np. sum (km.cluster_centers_,axis = 1 )

　　深入k-means

　　　　k-means在计算两条数据相似性时, 默认是使用欧式距离, 且没有给对应的参数来修改这个默认的计算距离的方法

　　　　如果需要修改这个默认的距离方式, 需要修改源代码

　　　　源码位置为C:\Python36\Lib\site-packages\sklearn\metrics\pairwise.py

　　　　162行的euclidean_distances()函数

　　　　建议使用scipy.spatial.distance.cdist方法

回到顶部

5 DBSCAN方法及应用

　　DBSCAN算法是一种基于密度的聚类算法

　　　　DBSCAN算法聚类的时候不要预先指定簇的个数

　　　　因而最终的簇的个数不确定

　　DBSCAN算法将数据点分为三类

　　　　核心点: 在半径Eps内含有超过MinPts数据的点

　　　　边界点: 在半径Eps内点的数量小于MinPts, 但是落在核心点的邻域内

　　　　噪音点: 既不是核心点也不是边界点的点

　　DBSCAN的算法流程

　　　　1.将所有点标记为核心点、边界点或噪声点;

　　　　2.删除噪声点;

　　　　3.为距离在Eps之内的所有核心点之间赋予一条边;

　　　　4.每组连通的核心点形成一个簇;

　　　　5.将每个边界点指派到一个与之关联的核心点的簇中(哪一个核心点的半径范围之内)

　　获得密度聚类的实例

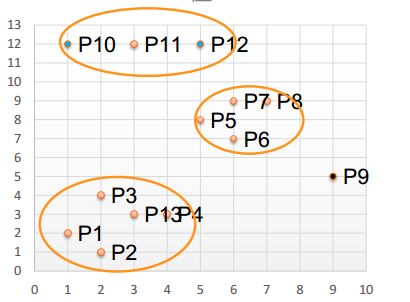
　　　　设Eps=3, MinPts=3, 采用曼哈顿距离聚类

　　　　

　　　　处理核心点, 边界点, 噪声点

　　　　

　　　　将不超过Eps=3的点相互圈起来形成一个簇, 核心点邻域内的点都会被加入到这个簇当中

　　　　

　　创建DBSCAN的实例

　　　　使用代码

sklearn.cluster.DBSCAN()

　　　　其中有几个参数

　　　　eps: 两个样本被看做邻居节点的最大距离

　　　　min_samples: 簇的样本数

　　　　metric: 距离的计算方式

　　　　详细介绍

　　创建完毕DBSCAN的对象之后

　　　　可以后 DBSCAN对象.fix(数据) 来生成一个结果, 这个结果有一个属性是labels_

　　　　这个就是我们需要的标签

 　　　　其中标签中值为-1表示噪声

　　实例处理, 学生上网时间分布

　　数据

　　　　

　　　　分别是 记录编号, 学生编号, MAC地址, IP地址, 开始上网时间, 结束上网时间, 上网时长(秒), …

　　具体代码

import numpy as np
import sklearn.cluster as skc
from sklearn import metrics
import matplotlib.pyplot as plt

onlinetimes = {}
with open ( "学生月上网时间分布-TestData.txt" , encoding = "utf8" ) as f:
    for line in f:
        info_list = line.strip().split( ',' )
        mac = info_list[ 2 ]
        onlinetime = int (info_list[ 6 ])
        # 获取上网的起始时候的小时 "2014-07-21 08:14:29.287000000" 这个的08
        starttime = int (info_list[ 4 ].split( ' ' )[ 1 ].split( ':' )[ 0 ])
        onlinetimes[mac] = (starttime, onlinetime)
real_X = np.array([onlinetimes[key] for key in onlinetimes]).reshape(( - 1 , 2 ))
# 只获取上网的时间点
X = real_X[:, 0 : 1 ]

db = skc.DBSCAN(eps = 0.01 , min_samples = 20 ).fit(X)
labels = db.labels_

# 获得噪声点比例
raito = len (labels[labels[:] = = - 1 ]) / len (labels)
print ( 'Noise raito:' , format (raito, '.2%' ))

# 显示算法性能
n_clusters_ = len ( set (labels)) - ( 1 if - 1 in labels else 0 )
print ( 'Estimated number of clusters: %d' % n_clusters_)
print ( "Silhouette Coefficient: %0.3f" % metrics.silhouette_score(X, labels))

for i in range (n_clusters_):
    print ( 'Cluster ' , i, ':' )
    print ( list (X[labels = = i].flatten()))

plt.hist(X, 24 )
plt.show()

　　实验结果

　　　　

　　处理数据的技巧

　　　　如果原始数据不协调, 不利于数据处理, 可以对原始数据进行无损变化来使得数据大小更加合适处理

　　　　具体的处理办法就是取对数变换

回到顶部

6  PCA方法及其应用

　　PCA(Principal Component Analysis), 主成分分析, 是最常用的一种降维方法, 通常用于高维数据集的探索与可视化, 还可以用作数据压缩和预处理等

　　PCA可以把具有相关性的高维变量合成为线性无关的低维变量，称为主成分。主成分能够尽可能保留原始数据的信息

　　相关术语

　　1) 方差

　　　　是各个样本和样本均值的差的平方和的均值，用来度量一组数据的分散程度

　　　　公式

　　　　

　　2) 协方差

　　　　用于度量两个变量之间的线性相关性程度，若两个变量的协方差为0，则可认为二者线性无关。协方差矩阵则是由变量的协方差值构成的矩阵（对称阵）

　　　　公式

　　　　

　　3) 特征向量

　　　　矩阵的特征向量是描述数据集结构的非零向量

　　　　公式

　　　　

　　主成分分析的原理

　　　　矩阵的主成分就是其协方差矩阵对应的特征向量，按照对应的特征值大小进行排序，最大的特征值就是第一主成分，其次是第二主成分，以此类推

　　使用PCA

　　　　创建PCA对象

sklearn.decomposition.PCA()

　　　　主要有两个参数

　　　　n_components: 指定主要成分的个数

　　　　svd_solver: 设置特征值分解的方法, 默认为auto, 其他可选的还有full, arpack, randomized

　　创建PCA对象之后, 可以通过调用fit_transform(data)函数传入需要降维的数据, 返回的数据就是降维之后处理完毕的数据

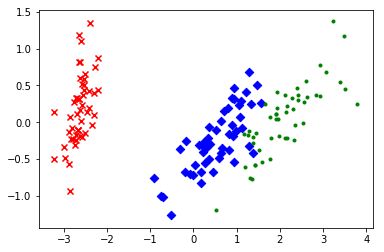
　　实例, 处理鸢尾花数据集

　　　　鸢尾花数据集是(150, 4)

　　　　可以利用PCA将数据集处理成(150, 2)的数据

　　　　处理鸢尾花数据让其从4维数据编程2位平面数据, 具体代码如下

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

data = load_iris()
y = data.target
X = data.data
pca = PCA(n_components = 2 )
reduced_X = pca.fit_transform(X)

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []

for i in range ( len (reduced_X)):
    if y[i] = = 0 :
        red_x.append(reduced_X[i][ 0 ])
        red_y.append(reduced_X[i][ 1 ])
    elif y[i] = = 1 :
        blue_x.append(reduced_X[i][ 0 ])
        blue_y.append(reduced_X[i][ 1 ])
    else :
        green_x.append(reduced_X[i][ 0 ])
        green_y.append(reduced_X[i][ 1 ])

plt.scatter(red_x, red_y, c = 'r' , marker = 'x' )
plt.scatter(blue_x, blue_y, c = 'b' , marker = 'D' )
plt.scatter(green_x, green_y, c = 'g' , marker = '.' )
plt.show()

　　具体结果

　　

回到顶部

7 NMF方法及其实例

　　NMF(Non-negative Matrix Factorization, 非负矩阵分解), 是在矩阵中所有元素均为非负数约束条件之下的矩阵分解方法

　　基本思想：给定一个非负矩阵V，NMF能够找到一个非负矩阵W和一个非负矩阵H，使得矩阵W和H的乘积近似等于矩阵V中的值

　　

　　W矩阵：基础图像矩阵, 相当于从原矩阵V中抽取出来的特征

　　H矩阵：系数矩阵

　　NMF能够广泛应用于图像分析、文本挖掘和语音处理等领域

　　

　　矩阵分解优化目标: 最小化W矩阵H矩阵的乘积和原始矩阵之间的差别，目标函数如下

　　

　　基于KL散度的优化目标, 损失函数如下

　　

　　公式的推导

　　在sklearn库中，可以使用sklearn.decomposition.NMF加载NMF算法，主要参数有

　　生成NMF对象

sklearn.decomposition.NMF()

　　　　n_components：用于指定分解后矩阵的单个维度k

　　　　init：W矩阵和H矩阵的初始化方式，默认为‘ nndsvdar’

　　使用NMF对人脸数据进行特征提取

　　　　使用 NMF对象.fit(数据) 来处理数据, 生成的内容还是在NMF对象中

　　　　获取处理数据 NMF对象.components_ 获取得到的数据

　　具体使用PCA和NMF处理人脸数据并且对比展示的代码如下

from numpy.random import RandomState
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn import decomposition

n_row, n_col = 2 , 3
n_components = n_row * n_col
image_shape = ( 64 , 64 )

# Load faces data
dataset = fetch_olivetti_faces(shuffle = True , random_state = RandomState( 0 ))
faces = dataset.data

def plot_gallery(title, images, n_col = n_col, n_row = n_row):
    plt.figure(figsize = ( 2. * n_col, 2.26 * n_row))
    plt.suptitle(title, size = 16 )
    for i, comp in enumerate (images):
        plt.subplot(n_row, n_col, i + 1 )
        vmax = max (comp. max (), - comp. min ())

        plt.imshow(comp.reshape(image_shape), cmap = plt.cm.gray,
                   interpolation = 'nearest' , vmin = - vmax, vmax = vmax)
        plt.xticks(())
        plt.yticks(())
    plt.subplots_adjust( 0.01 , 0.05 , 0.99 , 0.94 , 0.04 , 0. )


plot_gallery( "First centered Olivetti faces" , faces[:n_components])

estimators = [
    ( 'Eigenfaces - PCA using randomized SVD' ,
         decomposition.PCA(n_components = 6 ,whiten = True )),

    ( 'Non-negative components - NMF' ,
         decomposition.NMF(n_components = 6 , init = 'nndsvda' , tol = 5e - 3 ))
]

for name, estimator in estimators:
    print ( "Extracting the top %d %s..." % (n_components, name))
    print (faces.shape)
    estimator.fit(faces)
    components_ = estimator.components_
    plot_gallery(name, components_[:n_components])

plt.show()

回到顶部

8 基于聚类的“图像分割”

　　图像分割：利用图像的灰度、颜色、纹理、形状等特征，把图像分成若干个互不重叠的区域，并使这些特征在同一区域内呈现相似性，在不同的区域之间存在明显的差异性。 然后就可以将分割的图像中具有独特性质的区域提取出来用于不同的研究

　　图像分割技术已在实际生活中得到广泛的应用。例如：在机车检验领域，可以应用到轮毂裂纹图像的分割，及时发现裂纹，保证行车安全；在生物医学工程方面，对肝脏CT图像进行分割，为临床治疗和病理学研究提供帮助

　　图像分割常用方法：

　　　　1 阈值分割：对图像灰度值进行度量，设置不同类别的阈值，达到分割的目的

　　　　2 边缘分割：对图像边缘进行检测，即检测图像中灰度值发生跳变的地方，则为一片区域的边缘

　　　　3 直方图法：对图像的颜色建立直方图，而直方图的波峰波谷能够表示一块区域的颜色值的范围，来达到分割的目的

　　　　4 特定理论：基于聚类分析、小波变换等理论完成图像分割

　　实例描述

　　　　目标: 利用K-means聚类算法对图像像素点颜色进行聚类实现简单的图像分割 

　　　　输出: 同一聚类中的点使用相同颜色标记，不同聚类颜色不同

　　　　技术路线: sklearn.cluster.KMeans

　　具体代码

import numpy as np
import PIL.Image as image
from sklearn.cluster import KMeans

def loadData(filePath):
    f = open (filePath, 'rb' )
    data = []
    img = image. open (f)
    m,n = img.size
    for i in range (m):
        for j in range (n):
            x,y,z = img.getpixel((i,j))
            data.append([x / 256.0 ,y / 256.0 ,z / 256.0 ])
    f.close()
    return np.mat(data),m,n

imgData,row,col = loadData( 'kmeans/bull.jpg' )
label = KMeans(n_clusters = 4 ).fit_predict(imgData)

label = label.reshape([row,col])
pic_new = image.new( "L" , (row, col))
for i in range (row):
    for j in range (col):
        pic_new.putpixel((i,j), int ( 256 / (label[i][j] + 1 )))
pic_new.save( "result-bull-4.jpg" , "JPEG" )