深度学习2
文章目录
- 神经网络学习
- 损失函数
- 均方误差
- 交叉熵误差
- mini-batch学习
- 数值微分
- 导数公式
- 数值微分举例
神经网络学习
机器学习中,一般将数据分为训练数据和测试数据。训练数据也称为监督数据。
泛化能力是指处理未被观察过的数据(不包含在训练数据中的数据)的能力。
对某个数据集过度拟合的状态称为过拟合(over fitting)。
损失函数
损失函数(loss function)是表示神经网络性能的“恶劣程度”的指标,即当前的神经网络对监督数据在多大程度上不拟合,在多大程度上不一致。
均方误差
mean squared error
公式如下:
E = 1 2 ∑ k ( y k − t k ) 2 E=\frac{1}{2}\sum_{k} \left ( y_{k}-t_{k}\right )^{2} E=21k∑(yk−tk)2
y k y_{k} yk是表示神经网络的输出, t k t_{k} tk 表示监督数据, k k k 表示数据的维数。
交叉熵误差
cross entropy error
E = − ∑ k t k l o g y k E=-\sum_{k}{t_{k} \\log y_{k}} E=−k∑tklogyk
x等于1时,y为0;随着x向0靠近,y逐渐变小。
正确解标签对应的输出越大,交叉熵误差越接近0;当输出为1时,交叉熵误差为0。
正确解标签对应的输出较小,交叉熵误差较大。
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
参数y和t是NumPy数组,当出现np.log(0)时,np.log(0)会变为负无限大的-inf,故加上了一个微小值delta。
mini-batch学习
神经网络的学习也是从训练数据中选出一批数据(称为mini-batch, 小批量),然后对每个mini-batch 进行学习。
训练数据的损失函数的总和, 以交叉熵误差为例
E = − 1 N ∑ n ∑ k t n k l o g y n k E=-\frac{1}{N}\sum_{n}\sum_{k}{t_{nk} \\log y_{nk}} E=−N1n∑k∑tnklogynk
数据有 N N N个, t n k t_{nk} tnk 表示第 n n n个数据的第 k k k个元素的值( y n k y_{nk} ynk是神经网络的输出, t n k t_{nk} tnk 是监督数据)
通过除以 N N N,可以求单个数据的“平均损失函数”。通过这样的平均化,可以获得和训练数据的数量无关的统一指标。
使用np.random.choice()可以从指定的数字中随机选择想要的数字
>>> np.random.choice(60000, 10)
array([ 8013, 14666, 58210, 23832, 52091, 10153, 8107, 19410, 27260,21411])
同时处理单个数据和批量数据(数据作为batch 集中输入)两种情况
监督数据为one-hot表示 ,交叉熵误差代码实现如下:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
y是神经网络的输出,t是监督数据。
y的维度为1 时,即求单个数据的交叉熵误差时,需要改变数据的形状。
监督数据为标签形式(非one-hot表示),交叉熵误差代码实现如下:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
np.log( y[np.arange(batch_size), t] )
假设batch_size为5,np.arange(5)生成一个NumPy 数组[0, 1, 2, 3, 4]
t中标签是以[2, 7, 0, 9, 4]的形式存储的。
y[np.arange(batch_size), t] 会生成NumPy 数组[y[0,2], y[1,7], y[2,0],y[3,9], y[4,4]])。
>>> y=np.arange(36).reshape(6,6)
>>> y
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35]])
>>> t=np.array([5,4,3,2,1])
>>> a=y[np.arange(5),t]
>>> a
array([ 5, 10, 15, 20, 25])
数值微分
导数公式
d f ( x ) ) d x = f ( x + h ) − f ( x ) h \frac{\mathrm{d} f(x))}{\mathrm{d} x}=\frac{f(x+h)-f(x)}{h} dxdf(x))=hf(x+h)−f(x)
导数的实现
def numerical_diff(f, x):
h = 1e-50
return (f(x+h) - f(x)) / h
优化版
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
消除舍入误差(省略小数的精细部分的数值带来的误差)
数值微分含有误差,采用中心差分
数值微分举例
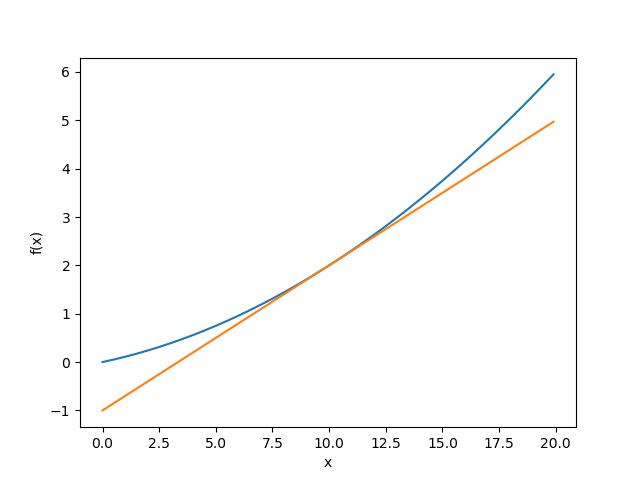
函数 y = 0.01 x 2 + 0.1 x y=0.01x^{2}+0.1x y=0.01x2+0.1x 在 x = 10 x=10 x=10处的导数及切线
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
return 0.01*x**2 + 0.1*x
def tangent_line(f, x):
d = numerical_diff(f, x)
print(d)
y = f(x) - d*x
print(y)
return lambda t: d*t + y
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
tf = tangent_line(function_1, 5)
y1 = tf(x)
plt.plot(x,y)
plt.plot(x,y1)
plt.show()
偏导数
f ( x 0 , x 1 ) = x 0 2 + x 1 2 f\left ( x_{0},x_{1} \right )= x_{0}^{2}+x_{1}^{2} f(x0,x1)=x02+x12