pytorch实战 ----线性回归

虽然大部分内容都是从github上找的。但是里面还是有些我自己的想法的，不喜勿喷，反正我主要是给自己看的。

数据准备

首先还是要导入一些库，matplotlib是画图的。torch.autograd是为了转换数据类型的，因为pytorch只能处理variable类型的数据，所以就算自己的数据也要转化为variable类型的。

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
from torch.autograd import Variable as V
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  
y = x.pow(2) + 0.2*torch.rand(x.size())                 
x,y = V(x),V(y)

神经网络结构

构造函数定义了两个线性结构，毕竟数据也是比较简单。激活函数有时加载构造函数中，有时加在向前传播函数中但是写法稍微不同。区别是如果模型有可学习的参数，最好用nn.Module，否则既可以使用nn.functional也可以使用nn.Module，二者在性能上没有太大差异，具体的使用取决于个人的喜好。如激活函数（ReLU、sigmoid、tanh），池化（MaxPool）等层由于没有可学习参数，则可以使用对应的functional函数代替，而对于卷积、全连接等具有可学习参数的网络建议使用nn.Module
对于神经网络的结构还是推荐用Sequential的写法，好处是当神经万罗结构很长时，写forward函数比较简单。

class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)  
        self.predict = torch.nn.Linear(n_hidden, n_output)   

    def forward(self, x):
        x = F.relu(self.hidden(x))      
        x = self.predict(x)            
        return x

net = Net(n_feature=1, n_hidden=10, n_output=1)
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()

训练及绘图

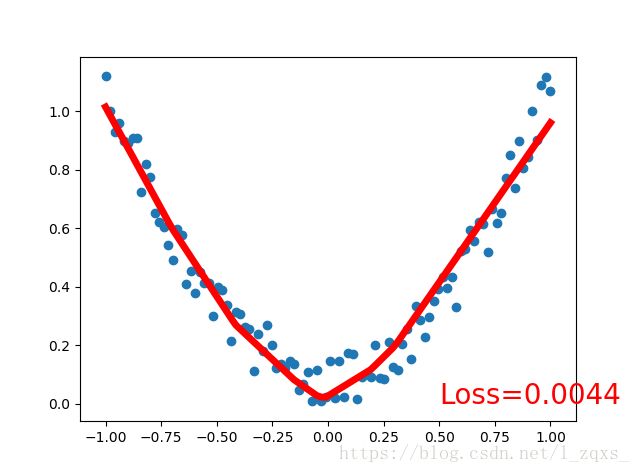
一开始我看到这个循环时，我不太明白加循环的意义。当时我觉得数据量这么少，肯定用不到批处理，而且循环变量根数据没什么关系。最近恍然大悟，咱们的目的是拟合函数，数据量少，一次就能用完，所以通过循环一遍又一遍（过拟合），这样才会逼近原数据。
说实话这种故意过拟合还是比较少见的，关于绘图的一些函数我写在注释里了，在一般的编译器中matplotlib是默认非交互的。
最后，把每段程序依次复制下俩就嫩那个成功的运行了。

plt.ion()   #打开交互模式
for t in range(200):
    prediction = net(x)     

    loss = loss_func(prediction, y)    

    optimizer.zero_grad()   
    loss.backward()         
    optimizer.step()   

    if t % 5 == 0:
        plt.cla()#即清除当前图形中的当前活动轴。其他轴不受影响
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

plt.ioff()#关闭交互模式
plt.show()