数据结构总结（全）

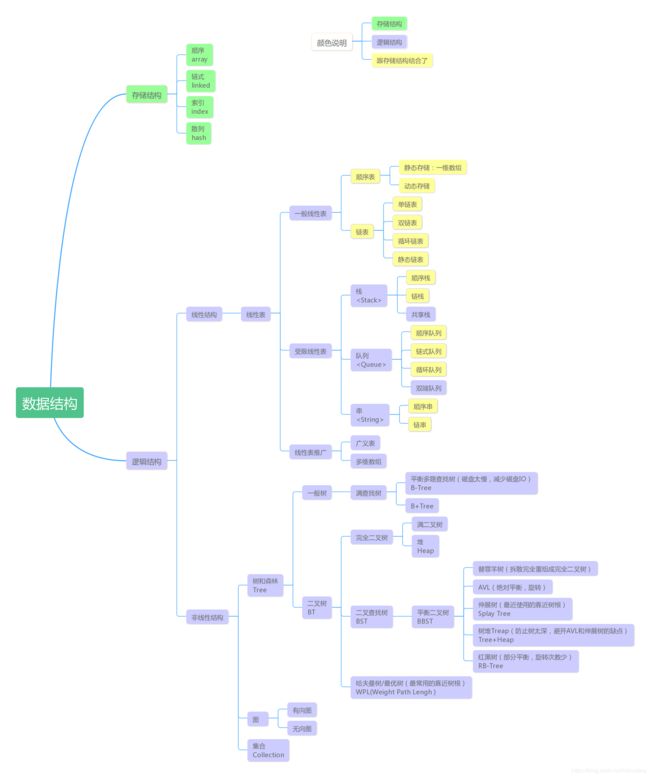
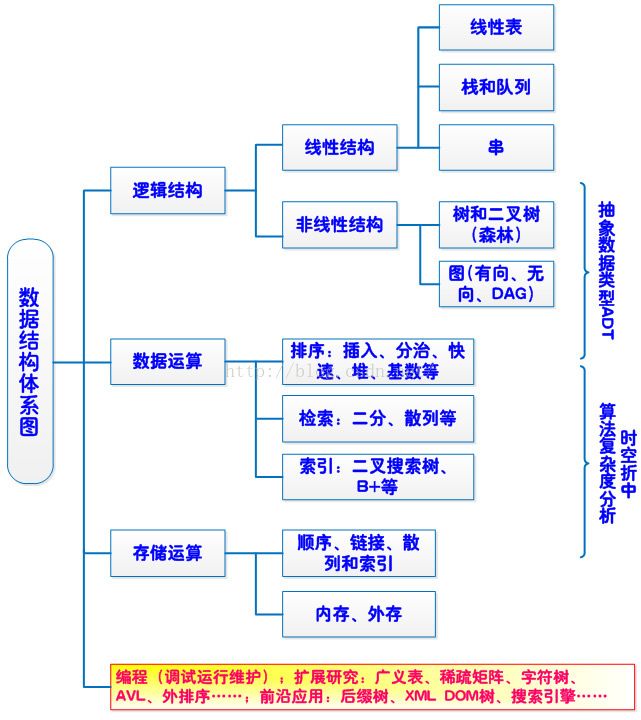
总分类，看图

标题

1 数据结构

       数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
       数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。记为：
Data_Structure=(D,R)，其中D是数据元素的集合，R是该集合中所有元素之间的关系的有限集合。

数据结构的由来

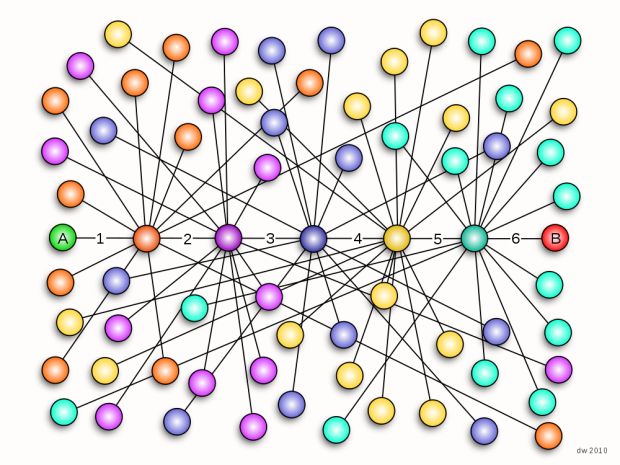
美国心理学家提出了一个六度分离理论。指的是 ‘’你和任何一个陌生人之间所间隔的人不会超过五个（100的6次方就是一百亿），也就是说，最多通过五个人你就能够认识任何一个陌生人。”根据这个理论，你和世界上的任何一个人之间只隔着五个人，不管对方在哪个国家，属哪类人种，是哪种肤色。

 

由此可见，我们生活在一个如蜘蛛网般错综复杂的世界，我们每个人并不是单独的个体，而是和其他人有联系的。在当今这个大数据时代，数据即财富。所以我们需要用计算机存储、分析大量的数据，提取出对我们来说有价值的数据。

我们每个人每天都在产生数据，例如我们在淘宝搜索了某个商品，购买了某本书等等。正如人和人之间有很多联系一样，数据和数据之间也会有许多联系，没有哪个数据是单独存在的，即使有，这种数据也没有利用价值，我们没有必要去分析，研究它。

数据结构恰恰就是用来囊括数据以及数据与之间关系的一种集合。如何把相关联的数据存储到计算机，为后续的分析提供有效的数据源，是数据结构产生的由来。数据结构就是计算机存储、组织数据的方式。好的数据结构，让我们做起事来事半功倍。精心选择的数据结构可以带来更高的计算速度和存储效率。

逻辑结构是面向问题的，而物理结构就是面向计算机的，其基本的目标就是将数据及其逻辑关系存储到计算机的内存中。

1.1 物理结构

数据的逻辑结构在计算机存储空间的存放形式被称为数据的物理结构。

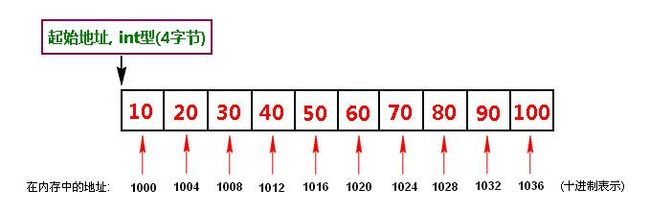
1.顺序存储结构

把逻辑上相邻的结点存储在物理位置上相邻的存储单元里，结点间的逻辑关系由存储单元的邻接关系来体现。在计算机中用一组地址连续的存储单元依次存储线性表的各个数据元素,称作线性表的顺序存储结构。

 

特点：

1、随机存取表中元素。

2、插入和删除操作需要移动元素。

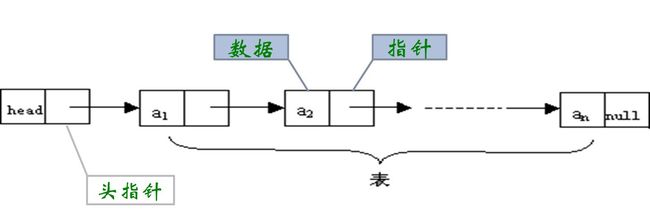
2.链接存储结构

在计算机中用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。它不要求逻辑上相邻的元素在物理位置上也相邻.因此它没有顺序存储结构所具有的弱点,但也同时失去了顺序表可随机存取的优点。

 

特点：

1、比顺序存储结构的存储密度小 (每个节点都由数据域和指针域组成，所以相同空间内假设全存满的话顺序比链式存储更多)。

2、逻辑上相邻的节点物理上不必相邻。

3、插入、删除灵活 (不必移动节点，只要改变节点中的指针)。

4、查找结点时链式存储要比顺序存储慢。

5、每个结点是由数据域和指针域组成。

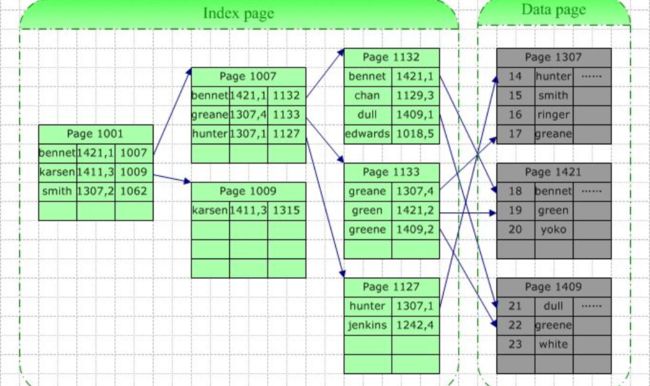
3.数据索引存储结构

除建立存储结点信息外，还建立附加的索引表来标识结点的地址。索引表由若干索引项组成，如果每个节点在索引表中都有一个索引项，则该索引表就被称为稠密索引。若一组节点在索引表中只对应于一个索引项，则该索引表就成为稀疏索引。索引项的一般形式一般是关键字、地址。在搜索引擎中，需要按某些关键字的值来查找记录，为此可以按关键字建立索引，这种索引就叫做倒排索引(因为是根据关键词来找链接地址，而不是通过某个链接搜索关键词，这里反过来了，所以称为倒排索引)，带有倒排索引的文件就叫做倒排索引文件，又称为倒排文件。倒排文件可以实现快速检索，这种索引存储方法是目前搜索引擎最常用的存储方法。

存储单词的过程：先在某个地址空间存储单词，然后把该单词的关键词和存储地址存到附加的索引表。

查找某个单词的过程：先根据关键词找索引表，得到数据存储地址。然后再通过存储地址得到数据。

特点：

索引存储结构是用结点的索引号来确定结点存储地址，其优点是检索速度快，缺点是增加了附加的索引表,会占用较多的存储空间。

4.数据散列存储结构

散列存储，又称hash存储，是一种力图将数据元素的存储位置与关键字之间建立确定对应关系的查找技术。比如将汤高这个名字通过一个函数转换成为一个值，这个值就是姓名汤高在计算机中的存储地址，这个函数称为hash函数。hash函数有很多种，今天先不谈。以后再细讲。

散列法存储的基本思想是：它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表

 

特点：

散列是数组存储方式的一种发展，相比数组，散列的数据访问速度要高于数组。要依据数据的某一部分来查找数据时数组一般要从头遍历数组才能确定想要查找的数据位置，而散列是通过函数通过“想要查找的数据”作为“输入”、“数据的位置”作为“输出”来实现快速访问，因此时间复杂度可以认为为O(1)，而数组遍历的时间复杂度为O(n)。

1.2 逻辑结构

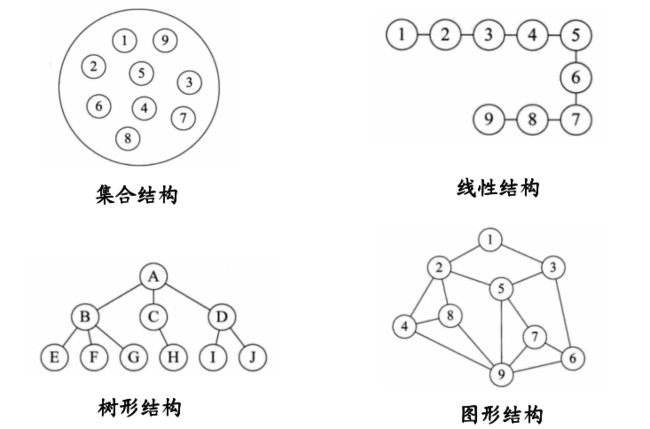
数据与数据之间的联系被称为数据的逻辑结构 ，根据关系的紧密程度，逻辑结构被分为四种

1.集合

数据结构中的元素之间除了“同属一个集合” 的相互关系外，别无其他关系。打个比方，我有一个篮子，篮子里面放了一个苹果，一个香蕉，一个梨子。这三种水果除了放在一个篮子里面，他们没有其它联系。这篮子里三种水果就属于一个集合，他们老死不相往来。

2.线性结构

数据结构中的元素存在一对一的相互关系；打个比方，我要高考了，但是我数学不好，所以我请了一个数学老师给我单独补课，并且规定在我补课期间，该数学老师不能跟其他人补课，那么我和这个数学老师就是一对一的关系，我们之间的关系就是他跟我补课。还比如排队，每列只站一个人，每列总共十个人，那么他们每个人之间有先后关系，但是都是一对一的先后关系。

第1章第1节 线性表的顺序表示：数组 https://blog.csdn.net/u013595419/article/details/50469346

第1章第2节 线性表的链式表示（1）单链表： https://blog.csdn.net/u013595419/article/details/50481785

第1章第2节 线性表的链式表示（2）双链表：https://blog.csdn.net/u013595419/article/details/50488122

第1章第2节 线性表的链式表示（3）循环链表和静态链表：https://blog.csdn.net/u013595419/article/details/50491780

第1章第3节 线性表的比较  https://blog.csdn.net/u013595419/article/details/50515255

 

第2章 受限的线性表：https://blog.csdn.net/u013595419/article/details/50516508

第2章第1节 栈： https://blog.csdn.net/u013595419/article/details/50518427

第2章第2节 队列：https://blog.csdn.net/u013595419/article/details/50523068

第2章第3节 串： https://blog.csdn.net/u013595419/article/details/50529017

 

 

第3章 线性表的推广： https://blog.csdn.net/u013595419/article/details/50803891

第3章第1节 数组的存储结构：https://blog.csdn.net/u013595419/article/details/50803912

 

3.树形结构

数据结构中的元素存在一对多的相互关系；比如，一个数学老师给两个或者多个学生补课，那么老师和学生之间就是一对多的关系。

第4章树与森林：https://blog.csdn.net/u013595419/article/details/51347703

第4章第1节 二叉树的基本概念：https://blog.csdn.net/u013595419/article/details/51465096

二叉搜索树：https://blog.csdn.net/u014634338/article/details/39102739

平衡二叉树（一般是AVL）图解与实现：https://blog.csdn.net/u014634338/article/details/42465089

伸展树(Splay tree)图解与实现：https://blog.csdn.net/u014634338/article/details/49586689
Treap(树堆)图解与实现：https://blog.csdn.net/u014634338/article/details/49612159

亲自动手画红黑树：https://blog.csdn.net/u014634338/article/details/78007490

二叉树的应用--哈夫曼树： https://blog.csdn.net/u014634338/article/details/39619959

伸展树(Splay tree)图解与实现https://blog.csdn.net/u014634338/article/details/49586689

红黑树和AVL树的比较  https://www.jianshu.com/p/37436ed14cc6

 

图解B树的前世今生：https://blog.csdn.net/u014634338/article/details/84886476

BTree和B+Tree详解：https://www.cnblogs.com/vianzhang/p/7922426.html

4.图形结构

数据结构中的元素存在多对多的相互关系。

比如我们的交通网，长沙有n条高速公路到达上海，同时上海也有k条高速公路到达长沙，长沙到上海是一对三n的关系，上海到长沙也是一对k的关系，所以长沙和上海是多对多的关系。

 

 

 

 

 

（一）常用结构 

1.数组:在程序设计中，为了处理方便， 把具有相同类型的若干变量按有序的形式组织起来。这些按序排列的同类数据元素的集合称为数组。在C语言中， 数组属于构造数据类型。一个数组可以分解为多个数组元素，这些数组元素可以是基本数据类型或是构造类型。因此按数组元素的类型不同，数组又可分为数值数组、字符数组、指针数组、结构数组等各种类别。

2.栈：(点击打开链接)是只能在某一端插入和删除的特殊线性表。它按照先进后出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。

3.队列:(点击打开链接)一种特殊的线性表，它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列是按照“先进先出”或“后进后出”的原则组织数据的。队列中没有元素时，称为空队列。

4.链表:是一种物理存储单元上非连续、非顺序的存储结构，它既可以表示线性结构，也可以用于表示非线性结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。

5.树:(点击打开链接)是包含n（n>0）个结点的有穷集合K，且在K中定义了一个关系N，N满足 以下条件：
（1）有且仅有一个结点 K0，他对于关系N来说没有前驱，称K0为树的根结点。简称为根（root）。　 

（2）除K0外，K中的每个结点，对于关系N来说有且仅有一个前驱。

（3）K中各结点，对关系N来说可以有m个后继（m>=0）。
6.图:（点击打开链接）是由结点的有穷集合V和边的集合E组成。其中，为了与树形结构加以区别，在图结构中常常将结点称为顶点，边是顶点的有序偶对，若两个顶点之间存在一条边，就表示这两个顶点具有相邻关系。

7.堆:在计算机科学中，堆是一种特殊的树形数据结构，每个结点都有一个值。通常我们所说的堆的数据结构，是指二叉堆。堆的特点是根结点的值最小（或最大），且根结点的两个子树也是一个堆。

8.散列表（Hash table，也叫哈希表）:（点击打开链接）若结构中存在关键字和K相等的记录，则必定在f(K)的存储位置上。由此，不需比较便可直接取得所查记录。称这个对应关系f为散列函数(Hash function)，按这个思想建立的表为散列表。

9.八大排序算法：（点击打开链接）排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。

 

 

 

（三）结构算法 
       算法的设计取决于数据（逻辑）结构，而算法的实现依赖于采用的存储结构。数据的存储结构实质上是它的逻辑结构在计算机存储器中的实现，为了全面的反映一个数据的逻辑结构，它在存储器中的映象包括两方面内容，即数据元素之间的信息和数据元素之间的关系。不同数据结构有其相应的若干运算。数据的运算是在数据的逻辑结构上定义的操作算法，如检索、插入、删除、更新和排序等。
       数据结构不同于数据类型，也不同于数据对象，它不仅要描述数据类型的数据对象，而且要描述数据对象各元素之间的相互关系。

       数据类型是一个值的集合和定义在这个值集上的一组操作的总称。数据类型可分为两类：原子类型、结构类型。一方面，在程序设计语言中，每一个数据都属于某种数据类型。类型明显或隐含地规定了数据的取值范围、存储方式以及允许进行的运算。可以认为，数据类型是在程序设计中已经实现了的数据结构。另一方面，在程序设计过程中，当需要引入某种新的数据结构时，总是借助编程语言所提供的数据类型来描述数据的存储结构。计算机中表示数据的最小单位是二进制数的一位，叫做位。我们用一个由若干位组合起来形成的一个位串表示一个数据元素，通常称这个位串为元素或结点。当数据元素由若干数据项组成时，位串中对应于各个数据项的子位串称为数据域。元素或结点可看成是数据元素在计算机中的映象。

一个软件系统框架应建立在数据之上，而不是建立在操作之上。一个含抽象数据类型的软件模块应包含定义、表示、实现三个部分。
对每一个数据结构而言，必定存在与它密切相关的一组操作。若操作的种类和数目不同，即使逻辑结构相同，数据结构能起的作用也不同。

不同的数据结构其操作集不同，但下列操作必不可缺：
1,结构的生成；
2.结构的销毁；
3,在结构中查找满足规定条件的数据元素；
4,在结构中插入新的数据元素；
5,删除结构中已经存在的数据元素；
6,遍历。
       抽象数据类型：一个数学模型以及定义在该模型上的一组操作。抽象数据类型实际上就是对该数据结构的定义。因为它定义了一个数据的逻辑结构以及在此结构上的一组算法。抽象数据类型可用以下三元组表示：（D，S，P）。D是数据对象，S是D上的关系集，P是对D的基本操作集。ADT的定义为：ADT 抽象数据类型名：{数据对象：（数据元素集合），数据关系：（数据关系二元组结合），基本操作：（操作函数的罗列）}； ADT抽象数据类型名;抽象数据类型有两个重要特性：

       数据抽象：用ADT描述程序处理的实体时，强调的是其本质的特征、其所能完成的功能以及它和外部用户的接口（即外界使用它的方法）。

       数据封装：将实体的外部特性和其内部实现细节分离，并且对外部用户隐藏其内部实现细节。

       数据（Data）是信息的载体，它能够被计算机识别、存储和加工处理。它是计算机程序加工的原料，应用程序处理各种各样的数据。计算机科学中，所谓数据就是计算机加工处理的对象，它可以是数值数据，也可以是非数值数据。数值数据是一些整数、实数或复数，主要用于工程计算、科学计算和商务处理等；非数值数据包括字符、文字、图形、图像、语音等。

       数据元素（Data Element）是数据的基本单位。在不同的条件下，数据元素又可称为元素、结点、顶点、记录等。例如，学生信息检索系统中学生信息表中的一个记录等，都被称为一个数据元素。有时，一个数据元素可由若干个数据项（Data Item）组成，例如，学籍管理系统中学生信息表的每一个数据元素就是一个学生记录。它包括学生的学号、姓名、性别、籍贯、出生年月、成绩等数据项。这些数据项可以分为两种：一种叫做初等项，如学生的性别、籍贯等，这些数据项是在数据处理时不能再分割的最小单位；另一种叫做组合项，如学生的成绩，它可以再划分为数学、物理、化学等更小的项。通常，在解决实际应用问题时是把每个学生记录当作一个基本单位进行访问和处理的。

       数据对象（Data Object）或数据元素类（Data Element Class）是具有相同性质的数据元素的集合。在某个具体问题中，数据元素都具有相同的性质（元素值不一定相等），属于同一数据对象（数据元素类），数据元素是数据元素类的一个实例。例如，在交通咨询系统的交通网中，所有的顶点是一个数据元素类，顶点A和顶点B各自代表一个城市，是该数据元素类中的两个实例，其数据元素的值分别为A和B。 数据结构（Data Structure）是指互相之间存在着一种或多种关系的数据元素的集合。在任何问题中，数据元素之间都不会是孤立的，在它们之间都存在着这样或那样的关系，这种数据元素之间的关系称为结构。

 

 

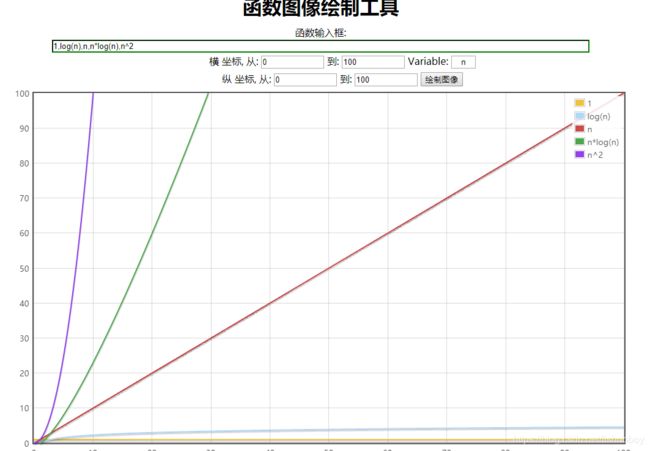
https://zh.numberempire.com/graphingcalculator.php

1,log(n),n,n*log(n),n^2