Colorful Image Colorization
这篇论文是加里福利亚大学Richard Zhang发表在ECCV 2016上的文章,论文的工作是灰度图的自动着色,这里博主想要重点关注一下论文对颜色分布预测的工作,所以把一篇这么老的论文翻出来重新看。
论文主页:http://richzhang.github.io/colorization/,东西比较全,论文,github,在线demo都有
1. 论文贡献
用论文作者自己的话说,论文贡献主要体现在两方面:
- 在自动图像着色的图形学领域取得了进步:设计了一个合适的损失函数来处理着色问题中的多模不确定性(简单来说就是物体可以有多种可能的上色),维持了颜色的多样性;介绍了一种新型的着色算法评估框架,而且这种评估框架有应用到其他图像合成任务的潜力;通过在百万数量级的彩色图片上训练在这类任务上抵达了一个新的水准。
- 将图像着色任务转化为一个自监督表达学习的任务,并且在一些基准上获得了最好的效果。
论文所做的事情用一句话就能概括:给灰度图上色。不过论文的切入点我觉得很巧妙,它不是恢复灰度图的真实颜色,而是用灰度图中物体的纹理、语义等信息作为线索,来预测可能的上色,最后的上色结果只要真实即可。这不仅降低了上色的难度,而且也符合人们的认知:比如一个苹果,给它上青色,上红色都是正常的,不限于某一个颜色,只要不是紫色黑色等奇怪的颜色。
2. 论文动机
考虑到这篇论文是发表于2016年,当时图像着色方面的工作还不是很多,已有的方法比如ICCV 2015的《Deep colorization》,可以看到下图中的上色结果,虽然大体上正确,但是颜色显得饱和度比较低,有些单调的感觉。Richard Zhang认为,前人的目标只是优化预测结果和真实图片间的欧氏距离(即MSE),这种损失函数会鼓励比较保守的预测(原因在后面会将),从而导致颜色饱和度不高,色彩不丰富。
《Very deep convolutional networks for large-scale image recognition》这篇文章指出,颜色预测是一个多模的问题,一个物体本来就可以上不同的颜色。为了对这种多模性建模,Richard Zhang为各个像素预测一个颜色的分布,这可以鼓励探索颜色的多样性,而不仅仅局限在某一种颜色中。
3. 论文模型
基本模型还是比较简单的,输入图片的 L L L通道,使用一个CNN预测对应的 a b ab ab通道取值的概率分布,最后转化为 R G B RGB RGB图像结果。网络模型这里不存在什么难点,下面着重看一下作者是怎么设计损失函数的。
损失函数
给定输入的 L L L通道 X ∈ R H × W × 1 X\in \mathbb{R}^{H\times W \times 1} X∈RH×W×1,现在的目标是学习一个到相应 a b ab ab通道 Y ∈ R H × W × 2 Y \in \mathbb{R}^{H \times W \times 2} Y∈RH×W×2的映射 Y ^ = F ( X ) \hat{Y}=\mathcal{F}(X) Y^=F(X)。最自然的一个想法是使用预测结果和真实图像间的 L 2 L_2 L2损失: (1) L 2 ( Y ^ , Y ) = 1 2 ∑ h , w ∥ Y h , w − Y ^ h , w ∥ 2 2 L_2(\hat{Y}, Y)=\frac{1}{2}\sum_{h,w}\|Y_{h, w}-\hat{Y}_{h,w}\|_2^2\tag{1} L2(Y^,Y)=21h,w∑∥Yh,w−Y^h,w∥22(1)但是这种损失函数对于着色问题的固有歧义和多模特性不是很鲁棒。如果一个物体可以上若干种颜色, L 2 L_2 L2损失函数的最优解将会是这几种颜色的平均值,直观上来看就是那些灰色的,不饱和的结果。而且,如果可能颜色所在的平面是非凸的,平均后的结果可能就会在平面之外,从而出现比较诡异的颜色(这里的平面可以理解为真实自然上色的解集)。
这篇论文将上色问题视为一个分类问题。首先将 a b ab ab通道的输出空间以10为步长量化为 Q = 313 Q=313 Q=313类,对于给定的输入 X X X,学习一个到颜色概率分布 Z ^ ∈ [ 0 , 1 ] H × W × Q \hat{Z} \in [0, 1]^{H \times W\times Q} Z^∈[0,1]H×W×Q的映射 Z ^ = G ( X ) \hat{Z}=\mathcal{G}(X) Z^=G(X)。
为了比较预测的结果 Z ^ \hat{Z} Z^和真实值的差距,我们定义一个函数 Z = H g t − 1 ( Y ) Z=\mathcal{H}^{-1}_{gt}(Y) Z=Hgt−1(Y)将真实颜色 Y Y Y转换成向量 Z Z Z(通过搜索最接近的分类将 Y Y Y变为One-Hot向量)。论文中的soft-encoding scheme是指在313类的输出空间中找到 Y h , w Y_{h,w} Yh,w的5个最近邻,并按照它们距离 Y h , w Y_{h,w} Yh,w的距离按比例进行高斯加权。最后使用多分类交叉熵作为损失函数: (2) L c l ( Z ^ , Z ) = − ∑ h , w v ( Z h , w ) ∑ q log ( Z ^ h , w , q ) L_{cl}(\hat{Z}, Z)=-\sum_{h,w}v(Z_{h,w})\sum_q\log(\hat{Z}_{h,w,q})\tag{2} Lcl(Z^,Z)=−h,w∑v(Zh,w)q∑log(Z^h,w,q)(2)其中 v ( ⋅ ) v(\cdot) v(⋅)是用来平衡那些出现频率较少的类的权重(下一节会将)。最后再使用函数 Y ^ = H ( Z ^ ) \hat{Y}=\mathcal{H}(\hat{Z}) Y^=H(Z^)将预测得到的概率分布 Z ^ \hat{Z} Z^映射到具体的颜色值 Y ^ \hat{Y} Y^(下下节中会讲)。
分类再平衡
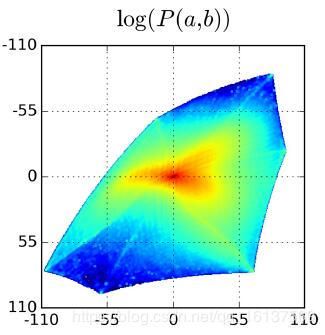
由于云朵、路面、沙漠等经常大面积地作为背景出现在图片中,自然图像中 a b ab ab的取值倾向于较小的方向。下图是从130万的数据集中统计的 a b ab ab取值分布,可以发现自然图片中取值都集中在不饱和区域,如果不考虑这个问题,那损失函数将会被不饱和的 a b ab ab取值主导。
为了处理这问题,作者在训练的时候为每个像素的loss重新调整权重,这个权重的大小是基于像素颜色的稀有度来设置的: (3) v ( Z h , w ) = w q ∗ q ∗ = arg max q Z h , w , q v(Z_{h,w})=w_{q*} q^*=\arg \max_q Z_{h,w,q}\tag{3} v(Zh,w)=wq∗ q∗=argqmaxZh,w,q(3) (4) w ∝ ( ( 1 − λ ) p ~ + λ Q ) − 1 E [ w ] = ∑ q p ~ q w q = 1 w\propto((1-\lambda)\tilde{p}+\frac{\lambda}{Q})^{-1} \mathbb{E}[w]=\sum_q\tilde{p}_qw_q=1\tag{4} w∝((1−λ)p~+Qλ)−1 E[w]=q∑p~qwq=1(4)为了得到平滑的经验分布 p ~ ∈ Δ Q \tilde{p}\in \Delta^Q p~∈ΔQ,作者统计了ImageNet训练集的 a b ab ab概率分布,并使用高斯核 G σ G_\sigma Gσ进行平滑。然后再用权重为 λ ∈ [ 0 , 1 ] \lambda \in [0,1] λ∈[0,1]的均匀分布进行混合并进行归一化。作者发现 λ = 1 2 , σ = 5 \lambda=\frac{1}{2},\sigma=5 λ=21,σ=5时效果比较好。
分类概率到点估计
最后,我们定义函数 H \mathcal{H} H,将预测的概率分布 Z ^ \hat{Z} Z^映射到 a b ab ab空间的点估计 Y ^ \hat{Y} Y^。一种方法是直接取每个像素,预测得到的模式,如下图最右边一列所示( T = 0 T=0 T=0),这种情况下能得到鲜艳的颜色,但是有时会出现颜色在空间上不连续,比如巴士上红色的点。如果取预测分布的平均值,将没有颜色不连续的现象,但是颜色的饱和度不高,显得不自然(最左边一列, T = 1 T=1 T=1)。造成这种低饱和度问题的原因和使用MSE损失是一样的,为了在这两者之前寻求一个平衡点,作者通过在softmax分布中引入参数 T T T,然后取结果的平均值: (5) H ( Z h , w ) = E [ f T ( Z h , w ) ] f T ( z ) = exp ( log ( z ) / T ) ∑ q exp ( log ( z q ) / T ) \mathcal{H}(Z_{h,w})=\mathbb{E}[f_T(Z_{h,w})] f_T(z)=\frac{\exp(\log(z)/T)}{\sum_q\exp(\log(z_q)/T)}\tag{5} H(Zh,w)=E[fT(Zh,w)] fT(z)=∑qexp(log(zq)/T)exp(log(z)/T)(5)参数 T T T的选择借鉴模拟退火的思想,最终选定 T = 0.38 T=0.38 T=0.38,效果如下图所示。
整个模型 F \mathcal{F} F最终包含两个部分:用于预测所有像素颜色分布的卷积神经网络 G \mathcal{G} G,和用于产生最终预测图像的退火平均操作 H \mathcal{H} H。虽然整个系统不能严格意义的端到端训练,但是可以注意到 H \mathcal{H} H是对每个像素单独作用的,只有一个参数,可以作为CNN的前向转播的一部分实现。
4. 论文实验
这篇论文的实验设计的还是蛮精心的,这里来好好学习一下。
上色质量评估
使用ImageNet的130万数据集训练,1万的验证集上测试。实验了不同Loss函数的效果,并和另外两种上色方法(Dahl, Larsson et al.)进行了对比,结果如下表所示:
下面来解释一下表格每一行具体代表什么:
- Ours(full):完整的模型,包括分类损失 L c l L_{cl} Lcl,分类再平衡
- Ours(class):损失函数只有分类损失 L c l L_{cl} Lcl,没有分类再平衡(式4中 λ = 1 \lambda=1 λ=1)
- Ours(L2):使用 L 2 L_2 L2损失函数
- Ours(L2,ft):在训练好的Ours(full)模型上,再使用 L 2 L_2 L2损失函数进行微调
- Gray:即 L L L通道, ( a , b ) = 0 (a,b)=0 (a,b)=0
- Random:从训练集中随机挑一张图片进行颜色复制
接下来再来看看使用了哪些评价指标。因为评价合成图像的质量缺少定量的指标,而RMS误差通常又难以衡量视觉真实性,作者使用了3种指标来总和评价:
- 视觉真实性( AMT):着色的最终目的是为了使图片看起来真实可信,为了衡量图像真实程度,作者设计了如下实验——随机给出一组图片(里面包含真实图片和着色后的图片),每次呈现两张图片,让人类受试者从中选择他们认为包含不自然颜色的图片。为了测试受试者是否有能力完成这项测试,使用随机上色的图片让受试者分辨。作者还贴心给出了一些例子帮助读者理解受试者的评判情况。(这个实验我是觉得没啥必要,随机上色的结果想想就知道很差了)
- 语义解释性(VGG分类):为了评价上色的真实性,作者还设计了另一个实验——使用现有的VGG分类器来对上色的图片进行分类。这种评价方法在CVPR 2016的一篇论文《Visually Indicated Sounds》提出用来评价合成数据的真实性。从表格数据来看,相比灰度图,上色后的分类正确率还是有提升的。然后作者得出这种上色方法还是有实用性的,我这里还是有所疑问,VGG本来就是用RGB图片训练分类的,用灰度图去分类自然效果不好,这里用上色后的图片去分类,效果有提升,这确实能证明上色后的效果比灰度图好,但总觉得这两者之间没啥必然的关联,毕竟瘦死的骆驼比马大嘛。
- 原始准确率(AuC):上面两个指标都是在真实性、语义这种高级层面上的评价,对于低级的指标,作者使用了真值图像和上色图像ab通道的 L 2 L_2 L2距离。然后后面解释的部分没咋看懂,明明 L 2 L_2 L2距离就只是衡量颜色预测的准确性的指标,然后作者说着说着就到了分类再平衡是有效果的?
自监督特征提取的交叉通道编码
为了进一步说明上色对于图形学任务的重要地位,作者解释了上色是如何作为表达学习的一种pretext task。这部分就不详细说了,作者就是把上色网络编码器的权重固定,然后重新训练成为一个分类、分割、识别网络,来检验这个上色网络特征学习的能力。
黑白照片的上色
为了阐述图片上色的应用价值,这里用的是黑白老照片上色。黑白老照片的灰度值分布和训练的 L L L通道图像还是有差别的,但是效果不错。