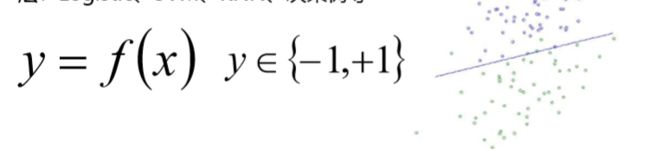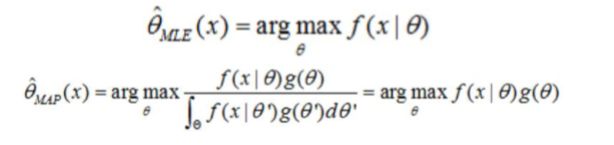一、单标签多分类
1、单标签二分类算法原理
1、单标签二分类这种问题是我们最常见的算法问题,主要是指label 标签的取值只有两种,并且算法中只有一个需要预测的label标签;
直白来讲就是每个实例的可能类别只有两种(A or B);此时的分类 算法其实是在构建一个分类线将数据划分为两个类别。
2、常见的算法:Logistic、SVM、KNN、决策树等
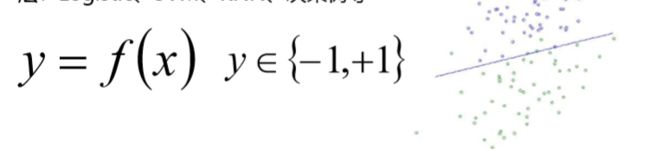
2、单标签多分类算法原理
1、单标签多分类问题其实是指待预测的label标签只有一个,但是 label标签的取值可能有多种情况;直白来讲就是每个实例的可能
类别有K种(t1,t2,...tk,k≥3);
2、常见算法:Softmax、SVM、KNN、决策树(集成学习 ----RF(Bagging)、Boosting(Adaboost、GBDT);XGBoost)
3、是一个多分类的问题,我们可以将这个待 求解的问题转换为二分类算法的延伸,即将多分类任务拆分为若 干个二分类任务求解,
具体的策略如下:
• One-Versus-One(ovo):一对一
• One-Versus-All / One-Versus-the-Rest(ova/ovr): 一对多
• Error Correcting Output codes(纠错码机制):多对多
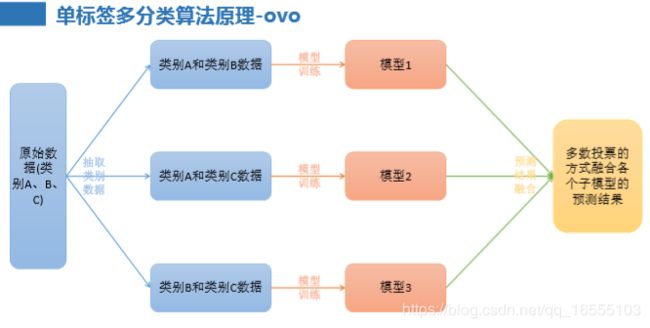
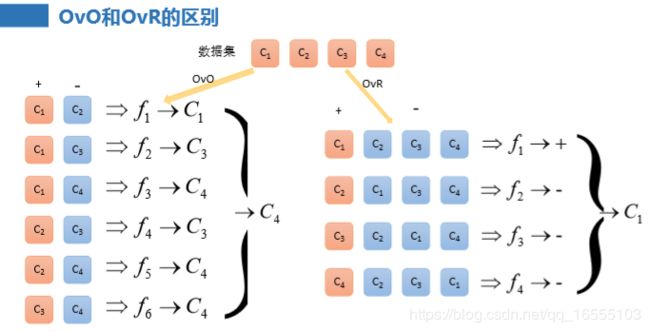
3、单标签多分类算法原理-ovo
• 原理:将K个类别中的两两类别数据进行组合,然后使用组合后的 数据训练出来一个模型,从而产生K(K-1)/2个分类器,将这些分类
器的结果进行融合,并将分类器的预测结果使用多数投票的方式 输出最终的预测结果值。
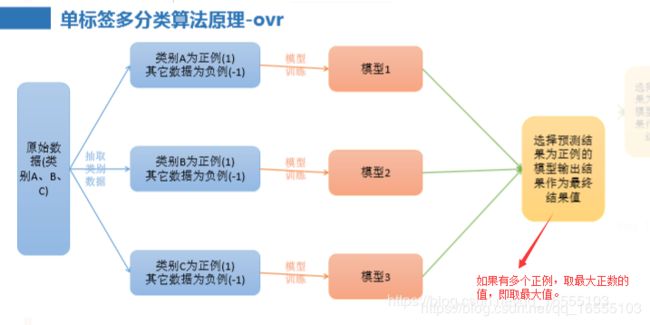
4、单标签多分类算法原理-ovr
1、ovr与softmax的区别:
① softmax 每一次训练模型用的是整个训练数据中的某一类别的数据,从而的该类别的权重系数,通过测试集计算各个类型权
重的预测值,取最大的预测值(或者概率)的类型作为预测类型。
② ovr 每一次是代入所有的训练集数据来训练子模型,取出结果为正例的类别(多个正例取最大值)。
5、OvO和OvR的区别
6、单标签多分类算法原理-Error Correcting
• 原理:将模型构建应用分为两个阶段:编码阶段和解码阶段;编 码阶段中对K个类别中进行M次划分,每次划分将一部分数据分 为
正类,一部分数据分为反类,每次划分都构建出来一个模型, 模型的结果是在空间中对于每个类别都定义了一个点;解码阶段
中使用训练出来的模型对测试样例进行预测,将预测样本对应的 点和类别之间的点求距离,选择距离最近的类别作为最终的预
测 类别。

二、多标签多分类
1、多标签多分类这类问题的解决方案可以分为两大类:
1) 转换策略(Problem Transformation Methods);
• Binary Relevance(first-order) --------- y标签之间相互独立
• Classifier Chains(high-order) --------- y标签之间相互依赖(链式)
• Calibrated Label Ranking(second-order) --------- 了解
2) 算法适应(Algorithm Adaptation)。
• ML-kNN
• ML-DT
1、 转换策略(Problem Transformation Methods)
1、转换策略思想:将多标签多分类问题转化为多个单标签二分类(通过哑编码转换 >>>>>>> -1 , +1 )的子模型,将这些子模
型的结果合并。
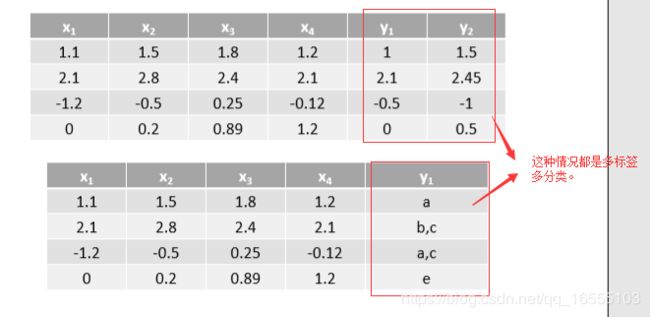
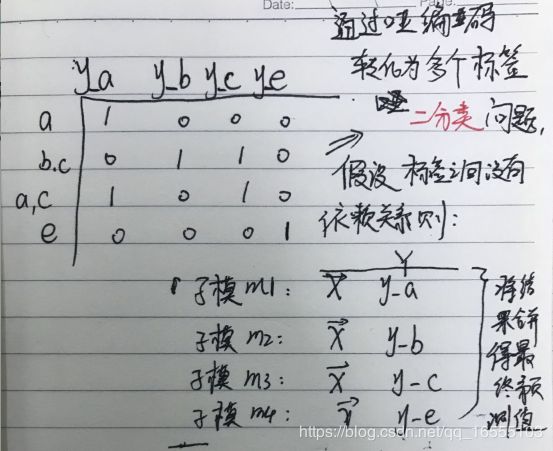
- Binary Relevance 与 Classifier Chains区别

---------------------------------------------------------------------------------------------
• Binary Relevance方式的优点如下:
• 实现方式简单,容易理解;
• 当y值之间不存在相关的依赖关系的时候,模型的效果不错。
• 缺点如下:
• 如果y直接存在相互的依赖关系,那么最终构建的模型的泛化能力比较 弱;
• 需要构建q个二分类器,q为待预测的y值数量,当q比较大的时候,需 要构建的模型会比较多。
---------------------------------------------------------------------------------------------
• Classifier Chains方式的优点如下:
• 实现方式相对比较简单,容易理解;
• 考虑标签之间的依赖关系,最终模型的泛化能力相对于Binary Relevance方 式构建的模型效果要好。
• 缺点如下:
• 很难找到一个比较适合的标签依赖关系。
---------------------------------------------------------------------------------------------
• Calibrated Label Ranking 方式的优点如下:
• 考虑了标签两两组合的情况,最终的模型相对来讲泛化能力比较好。
• 缺点如下:
• 只考虑两两标签的组合,没有考虑到标签与标签之间的所有依赖关系。
2、算法适应性
1、ML-kNN的思想:对于每一个实例来讲,先获取距离它最近的k个实例,然 后使用这些实例的标签集合,通过最大后验概率(MAP)来
断这个实例的 预测标签集合的值。
2、最大后验概率估计(MAP)贝叶斯估计 与 最大似然估计(MLE)区别?
答:最大后验概率(MAP)贝叶斯估计:其实就是在最大似然估计(MLE,样本划分目标属性Y的概率不是处处相等)中加入了这个要估
计量的先验概率分布(即样本划分目标属性Y的概率不是处处相等)。
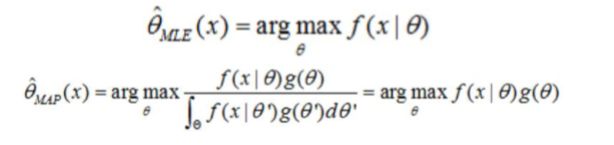
三、API的使用
1、单标签多分类
from sklearn.multiclass import OneVsRestClassifier,OneVsOneClassifier,OutputCodeClassifier
class sklearn.multiclass.OneVsRestClassifier(estimator, n_jobs=1)
'''
estimator ------- 子模型
n_jobs=1 ------- CPU使用
'''
class sklearn.multiclass.OneVsOneClassifier(estimator, n_jobs=1)
class sklearn.multiclass.OutputCodeClassifier(estimator, code_size=1.5, random_state=None, n_jobs=1)
2、多标签多分类
from sklearn.multiclass import XXX
class sklearn.multioutput.MultiOutputClassifier(estimator, n_jobs=1) ----- 没有依赖关系的多标签多分类
class sklearn.multioutput.MultiOutputRegressor(estimator, n_jobs=1)