> rm(list = ls())
> library(openxlsx)
> electric= read.xlsx("data101.xlsx",sheet = 1) #打开文件
> electric
No x y
1 1 679 0.79
2 2 292 0.44
3 3 1012 0.56
4 4 493 0.79
5 5 582 2.70
6 6 1156 3.64
7 7 997 4.73
8 8 2189 9.50
9 9 1097 5.34
10 10 2078 6.85
11 11 1818 5.84
12 12 1700 5.21
13 13 747 3.25
14 14 2030 4.43
15 15 1643 3.16
16 16 414 0.50
17 17 354 0.17
18 18 1276 1.88
19 19 745 0.77
20 20 435 1.39
21 21 540 0.56
22 22 874 1.56
23 23 1543 5.28
24 24 1029 0.64
25 25 710 4.00
26 26 1434 0.31
27 27 837 4.20
28 28 1748 4.88
29 29 1381 3.48
30 30 1428 7.58
31 31 1255 2.63
32 32 1777 4.99
33 33 370 0.59
34 34 2316 8.19
35 35 1130 4.79
36 36 463 0.51
37 37 770 1.74
38 38 724 4.10
39 39 808 3.94
40 40 790 0.96
41 41 783 3.29
42 42 406 0.44
43 43 1242 3.24
44 44 658 2.14
45 45 1746 5.71
46 46 468 0.64
47 47 1114 1.90
48 48 413 0.51
49 49 1787 8.33
50 50 3560 14.94
51 51 1495 5.11
52 52 2221 3.85
53 53 1526 3.93
求λ的第一种方法,用包
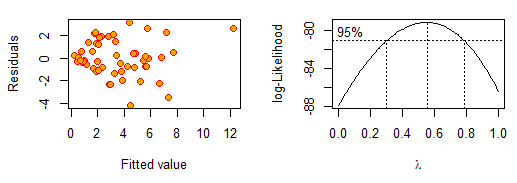
library(MASS) #MASS包有box-cox变换 op<-par(mfrow=c(2,2),mar=0.4+c(4,4,1,1),oma=c(0,0,2,0)) #将四张图放在一起,调整边界。(以后也采用此行) #绘制拟合值与残差的散点图(图1) plot(fitted(lm4.sol),resid(lm4.sol),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals") #box-cox变换 a1=boxcox(lm4.sol,lambda=seq(0,1,by=0.1)) #进行box-cox变换(图2)
根据box-cox指令画出来的图,λ=0.5包含在区间中,于是令λ=0.5
#### lambda=0.5 ####
lambda=0.5
Ylam<-(y^lambda-1)/lambda #对回归响应变量Y作变换
lm.lam<-lm(Ylam~x) #对变换后的响应变量与回归变量作回归
summary(lm.lam)
#绘制拟合值与残差的散点图
plot(fitted(lm.lam),resid(lm.lam),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals")
beta0=lm.lam$coeff[1]
beta1=lm.lam$coeff[2]
#绘制变换后函数曲线
curve( (1+lambda*(beta0+beta1*x))^(1/lambda),from=min(x),to=max(x),col="blue",lwd=2,xlab="能耗",ylab="用电需求量")
points(x,y,pch=21,cex=1.2,col="red", bg="orange")
mtext("Box-Cox Transformations",outer=T,cex=1.5) #四幅图的总标题
求λ的第二种方法
(1)对给定的λ,计算z(λ)
(2)求残差平方和
(3)对一系列的λ值,重复上述步骤,得到响应的残差平方和。以λ为横轴,残差平方和为纵轴,做出响应的曲线,值观看出使得残差平方和最小的λ
(4)求β*
lamb=c(-2,-1,-0.5,0,0.125,0.25,0.375,0.5,0.625,0.75,1,2)
### lamb=seq(-1,1,length=100)
n=length(x) #数据x的长度
k=length(lamb) #数据λ的长度
z=numeric(n) #构造一个长度为n的数字向量
SS=numeric(k) #构造一个长度为k的数字向量
X=matrix(c(rep(1,n),x),nr=n,nc=2) #设计矩阵
N=diag(n)-X%*%solve(crossprod(X))%*%t(X) #I-H
#求y的变换后的值
for(i in 1:k){
if(lamb[i]==0){
z= log(y)*(prod(y)^(1/n))
} else{
z=(y^lamb[i])/((prod(y))^((lamb[i]-1)/n))
}
SS[i]=z %*% N %*% z
}
SS ###SS[5]=1.84684 lamb=0.125
plot(lamb,SS,type='l')