动态规划理论学习

1. 理论总结

动态规划理论总结为“一个模型、三个特征”。

1.1 “一个模型”

• 它指的是动态规划适合解决的问题的模型。我把这个模型定义为“多阶段决策最优解模型"。
• 一般是用动态规划来解决最优问题。
• 解决问题的过程，需要经历多个决策阶段。每个决策阶段对应着一组状态。
• 然后我们寻找一组决策序列，经过这组决策序列，能够产生最终期望求解的最优值。

1.2 “三个特征”

1.2.1 最优子结构

• 问题的最优解包含子问题的最优解。
• 反过来说就是，可以通过子问题的最优解，推导出问题的最优解。后面阶段的状态可以通过前面阶段的状态推导出来。

1.2.2 无后效性

• 在推导后面阶段的状态时，我们只关心前面阶段的状态值，不关心这个状态是怎么一步一步推导出来的。
• 某阶段状态一旦确定，就不受之后阶段的决策影响。只要满足前面提到的动态规划问题模型，其实基本上都会满足无后效性。

1.2.3 重复子问题

• 不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。

2. 实例剖析

2.1 问题描述

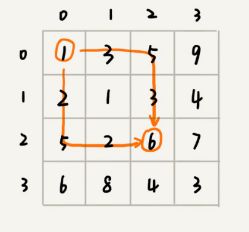
一个n乘以n的矩阵w[n][n]。存储的都是正整数。棋子起始位置在左上角，终止位置在右下角。每次只能向右或者向下移动一位。把每条路径经过的数字加起来看作路径的长度。最短路径长度是多少？

• 是否符合“一个模型”

1. 从（0，0）走到（n-1，n-1），总共要走 2n-1 步，对应着 2n-1 个阶段。
2. 每个阶段都有向右或向下走两种决策，并且每个阶段都会对应一个状态集合。
3. 我们把状态定义为 min_dist（i，j），其中 i 表示行，j 表示列。min_dist 表达式的值表示从（0，0）到达（i，j）的最短路径长度。
4. 所以，这个问题是一个多阶段决策最优解问题，符合动态规划的模型。
   

• 是否符合“三个特征”

1. 我们可以用回溯算法来解决这个问题。自己写一下代码，画一下递归树，就会发现，递归树中有重复的节点。重复的节点表示，从左上角到节点对应的位置，有多种路线，这也能说明这个问题中存在重复子问题。

   

下面给出回溯解法

/**
 * @description: dp课第二节，案例回溯法求解
 * @author: michael ming
 * @date: 2019/7/19 19:55
 * @modified by: 
 */
#include 
#define N 4//地图大小
#define k (2*N-1)//需要走的步数
using namespace std;
int selectWay[k], shortestWay[k];
void step(int (*map)[N], int s, int &mins, int r, int c, int idx)
{
    selectWay[idx++] = map[r][c];//记录选择的路
    if(r == N-1 && c == N-1)
    {
        if(s < mins)
        {
            mins = s;//更新最小的总路程
            for(int i = 0; i < k; ++i)//把最终的路线记录下来
                shortestWay[i] = selectWay[i];
        }
        return;
    }
    if(r == N || c == N)
        return;//走出地图边界了
    step(map,s+map[r+1][c],mins,r+1,c,idx);//往下走
    step(map,s+map[r][c+1],mins,r,c+1,idx);//往右走
}
int main()
{
    int s = 0, mins = 65535;
    int map[N][N] = {1,3,5,9,2,1,3,4,5,2,6,7,6,8,4,3};
    step(map,s+map[0][0],mins,0,0,0);
    cout << "最短路径是：" << mins << endl;
    cout << "走过的点的距离分别是：" << endl;
    for(int i = 0; i < k; ++i)
        cout << shortestWay[i] << " ";
    return 0;
}

2. 走到（i，j）这个位置，只能通过（i-1，j），（i，j-1）这两个位置移动过来，也就是，想要计算（i，j）位置对应的状态，只需关心（i-1，j），（i，j-1）两个位置对应的状态，并不关心棋子是通过什么样的路线到达这两个位置。而且，我们仅仅允许往下和往右移动，不允许后退，所以，前面阶段的状态确定后，不会被后面的决策所改变，所以，这个问题符合“无后效性”这一特征。

3. 把从起始位置（0，0）到（i，j）的最小路径，记作函数min_dist（i，j）。因为只能往右或往下移动，所以只有可能从（i，j-1）或（i-1，j）两个位置到达（i，j）。到达（i，j）的最短路径肯定包含到达这两个位置的最短路径之一。换句话说就是，min_dist（i，j）可以通过min_dist（i，j-1）和min_dist（i-1，j）两个状态推导出来。这就说明，这个问题符合“最优子结构”。

   min_dist(i, j) = w[i][j] + min{min_dist(i, j-1), min_dist(i-1, j)}
   

2.2 两种DP解题思路

2.2.1 状态转移表

• 一般能用动态规划的，都可以使用回溯暴力搜索。所以，可以先用简单的回溯算法解决，然后定义状态，对应画出递归树。

• 从递归树中，我们很容易可以看出来，是否存在重复子问题，以及重复子问题是如何产生的。以此来寻找规律，看是否能用动态规划解决。

• 找到重复子问题之后，有两种处理思路，第一种是回溯加“备忘录”的方法，来避免重复子问题。从效率上来讲，这跟动态规划的解决思路没有差别。

• 第二种是使用动态规划，状态转移表法。

• 先画出一个状态表，一般是二维的，可以把它想象成二维数组。其中，每个状态包含三个变量，行、列、数组值。

• 根据决策的先后，从前往后，根据递推关系，分阶段填充状态表中的每个状态。最后，将这个递推填表的过程，翻译成代码，就是动态规划代码。

• 尽管大部分状态表都是二维的，如果问题的状态比较复杂，需要很多变量来表示，那对应的状态表就是高维的，这个时候，不适合用状态转移表法来解决了。一方面高维状态转移表不好画图表示，另一方面人脑不擅长思考高维的东西。

1. 根据回溯代码画出递归树，递归树中，一个状态（节点）包含三个变量（i，j，dist），其中i，j表示行和列，dist表示从起点到达点（i，j）的路径长度。图中看出，尽管（i，j，dist）不存在重复，但是（i，j）重复的有很多。对（i，j）重复的节点，我们只选择 dist最小的节点，继续递归求解，其他节点舍弃。
   

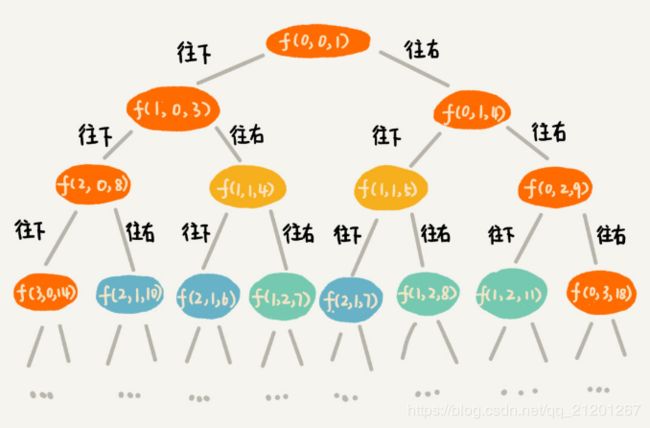
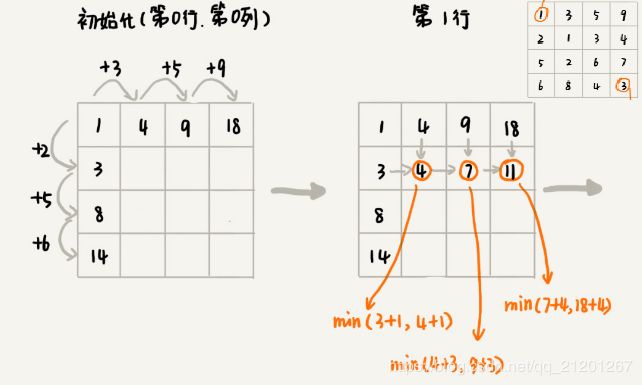
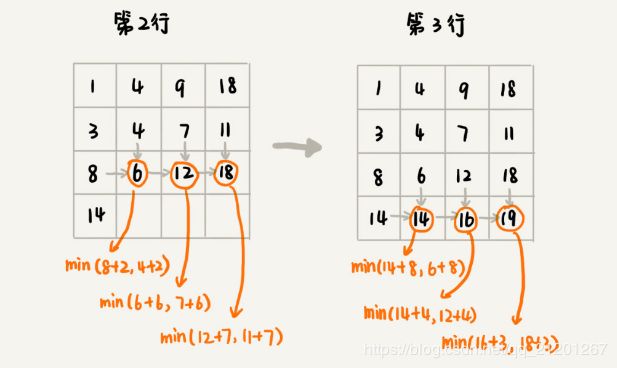
2. 画出二维状态表，表中行、列表示棋子位置，表中数值表示从起点到这个位置的最短路径。我们按照决策过程，将状态表填好。为了方便，我们按行来进行依次填充。

   
   

   dp状态表法代码如下：

   /**
    * @description: 
    * @author: michael ming
    * @date: 2019/7/19 23:30
    * @modified by: 
    */
   #include 
   #include 
   #define N 4//地图大小
   using namespace std;
   void printShortestWay(int (*map)[N], int (*states)[N])
   {
       stack<int> path;
       path.push(map[N-1][N-1]);//终点
       for(int i = N-1,j = N-1; j != 0 && i != 0; )
       {
           if(states[i][j]-map[i][j] == states[i-1][j])
               path.push(map[--i][j]);//从上面过来的
           else
               path.push(map[i][--j]);//从左边过来的
       }
       path.push(map[0][0]);//起点
       cout << "走过的点的距离分别是：" << endl;
       while(!path.empty())//栈逆序弹出路径
       {
           cout << path.top() << " ";
           path.pop();
       }
   }
   void step_dp(int (*map)[N])
   {
       int (*states)[N] = new int [N][N];
       int i, j, sum = 0;
       for(j = 0; j < N; ++j)//初始化第一行状态
       {
           sum += map[0][j];
           states[0][j] = sum;
       }
       sum = 0;
       for(i = 0; i < N; ++i)//初始化第一列状态
       {
           sum += map[i][0];
           states[i][0] = sum;
       }
       for(i = 1; i < N; ++i)//填写状态表
           for(j = 1; j < N; ++j)
               states[i][j] = map[i][j]+min(states[i][j-1],states[i-1][j]);
       cout << "最短路径是：" << states[N-1][N-1] << endl;
       printShortestWay(map,states);
       delete [] states;
       return;
   }
   int main()
   {
       int map[N][N] = {1,3,5,9,2,1,3,4,5,2,6,7,6,8,4,3};
       step_dp(map);
       return 0;
   }
   

   

2.2.2 状态转移方程

• 状态转移方程法有点类似递归。根据最优子结构，写出递归公式，也就是状态转移方程。

• 有两种代码实现方法，一种是递归加“备忘录”，另一种是迭代递推。

  min_dist(i, j) = w[i][j] + min{min_dist(i, j-1), min_dist(i-1, j)}
  

• 状态转移方程是解DP的关键。如果能写出状态转移方程，那DP问题基本上就解决一大半了。但是很多DP问题的状态本身就不好定义，状态转移方程也就更不好想到。

下面用递归加“备忘录”的方式，将状态转移方程翻译成代码。对于另一种实现方式，跟状态转移表法的代码实现是一样的，只是思路不同。

/**
 * @description: dp 状态方程 递归
 * @author: michael ming
 * @date: 2019/7/20 9:35
 * @modified by: 
 */
#include 
#include 
#define N 4//地图大小
using namespace std;
int states [N][N];
void printShortestWay(int (*map)[N])
{
    stack<int> path;
    path.push(map[N-1][N-1]);//终点
    for(int i = N-1,j = N-1; j != 0 && i != 0; )
    {
        if(states[i][j]-map[i][j] == states[i-1][j])
            path.push(map[--i][j]);//从上面过来的
        else
            path.push(map[i][--j]);//从左边过来的
    }
    path.push(map[0][0]);//起点
    cout << "走过的点的距离分别是：" << endl;
    while(!path.empty())//栈逆序弹出路径
    {
        cout << path.top() << " ";
        path.pop();
    }
}
int minDist(int (*map)[N], int i, int j)//从起点到i,j点的最小距离
{
    if(i == 0 && j == 0)//从起点到起点，返回该位置数值
        return map[0][0];
    if(states[i][j] > 0)//遇到算过的，直接返回结果
        return states[i][j];
    int minLeft, minUp;
    minLeft = minUp = 65535;
    if(j-1 >= 0)
        minLeft = minDist(map,i,j-1);//点左边的点的最小距离
    if(i-1 >= 0)
        minUp = minDist(map,i-1,j);//点上面的点的最小距离
    int currMinDist = map[i][j]+min(minLeft,minUp);
    states[i][j] = currMinDist;//备忘录更新
    return currMinDist;
}
int main()
{
    int map[N][N] = {1,3,5,9,2,1,3,4,5,2,6,7,6,8,4,3};
    cout << "最短路径是：" << minDist(map,N-1,N-1) << endl;
    printShortestWay(map);
    return 0;
}

强调一点，不是每个问题都同时适合这两种解题思路。有的问题可能用状态表更清晰，而有的问题可能用状态方程思路更清晰。

3. 四种算法思想比较

到现在为止，已经学习了四种算法思想，贪心、分治、回溯、动态规划。

• 贪心、回溯、动态规划，都可以抽象成多阶段决策最优解模型
• 而分治解决的问题尽管大部分也是最优解问题，但是，大部分都不能抽象成多阶段决策模型

算法	算法特点
回溯	穷举所有的情况，然后对比得到最优解。时间复杂度非常高，指数级，只能用来解决小规模问题。大规模问题，执行效率很低
动态规划	需要满足三个特征，最优子结构、无后效性和重复子问题，动态规划之所以高效，是因为回溯算法实现中存在大量的重复子问题
分治	要求分割成的子问题，不能有重复子问题，与动态规划正好相反
贪心	高效，代码简洁。可以解决的问题也有限。需要满足三个条件，最优子结构、无后效性和贪心选择性。“贪心选择性”的意思是，通过局部最优的选择，能产生全局的最优选择。每一个阶段，都选择当前看起来最优的决策，所有阶段的决策完成之后，最终由这些局部最优解构成全局最优解