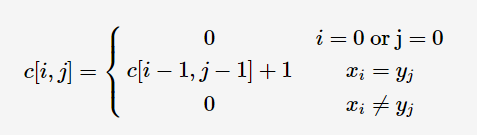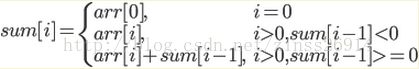动态规划经典问题总结
1.硬币找零
假设有几种硬币,如1、3、5,并且数量无限。请找出能够组成某个数目的找零所使用最少的硬币数。
这是一道经典的动态规划方法,我们可以维护一个一维动态数组dp,其中dp[i]表示钱数为i时的最小硬币数的找零,递推式为:dp[i] = min(dp[i], dp[i - coins[j]] + 1);
其中coins[j]为第j个硬币,而i - coins[j]为钱数i减去其中一个硬币的值,剩余的钱数在dp数组中找到值,然后加1和当前dp数组中的值做比较,取较小的那个更新dp数组。
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int Max = amount + 1;
vector<int> dp(amount + 1, Max);
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
for (int j = 0; j < coins.size(); j++) {
if (coins[j] <= i) {
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
};假设有几种硬币,每个值代表一张钱的面值,再给定一个整数代表要找的钱数,求换钱有多少种方法。
一个硬币一个硬币的增加,每增加一个硬币,都从1遍历到amount,对于遍历到的当前钱数j,组成方法就是不加上当前硬币的频发dp[i-1][j],还要加上,去掉当前硬币值的钱数的组成方法,当然钱数j要大于当前硬币值,那么我们的递推公式为:dp[i][j] = dp[i - 1][j] + (j >= coins[i - 1] ? dp[i][j - coins[i - 1]] : 0)
注意我们要初始化每行的第一个位置为1。
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<vector<int>> dp(coins.size() + 1, vector<int>(amount + 1, 0));
dp[0][0] = 1;
for (int i = 1; i <= coins.size(); ++i) {
dp[i][0] = 1;
for (int j = 1; j <= amount; ++j) {
dp[i][j] = dp[i - 1][j] + (j >= coins[i - 1] ? dp[i][j - coins[i - 1]] : 0);
}
}
return dp[coins.size()][amount];
}
};扩展:
一个矩形区域被划分为N*M个小矩形格子,在格子(i,j)中有A[i][j]个苹果。现在从左上角的格子(1,1)出发,要求每次只能向右走一步或向下走一步,最后到达(N,M),每经过一个格子就把其中的苹果全部拿走。请找出能拿到最多苹果数的路线。
分析:这道题中,当前位置(i,j)是状态,用M[i][j]来表示到达状态(i,j)所能得到的最多苹果数,那么M[i][j] = max(M[i-1][j],M[i][j-1]) + A[i][j] 。特殊情况是M[1][1]=A[1][1],当i=1且j!=1时,M[i][j] = M[i][j-1] + A[i][j];当i!=1且j=1时M[i][j] = M[i-1][j] + A[i][j]。
2. 字符串相似度/编辑距离
给定两个字word1和word2,找到将word1转换为word2所需的最小步骤数。 (每个操作计为1步)。
您对单词允许以下3种操作:
a)插入字符
b)删除字符
c)替换字符
dp[i][j]指把word1[0..i - 1]转换为word2[0..j - 1] 的最小操作数。
边界条件:
dp[i][0] = i; 从长度为 i 的字符串转为空串 要删除 i 次
dp[0][j] = j. 从空串转为长度为 j 的字符串 要添加 j 次
一般情况:
如果word[i - 1] == word2[j - 1],则dp[i][j] = dp[i - 1][j - 1],因为不需要进行操作,即操作数为0.
如果word[i - 1] != word2[j - 1],则需考虑三种情况,取最小值:
Replace word1[i - 1] by word2[j - 1]: (dp[i][j] = dp[i - 1][j - 1] + 1 (for replacement));
Delete word1[i - 1]: (dp[i][j] = dp[i - 1][j] + 1 (for deletion));
Insert word2[j - 1] to word1[0..i - 1]: (dp[i][j] = dp[i][j - 1] + 1 (for insertion)).
class Solution {
public:
int minDistance(string word1, string word2) {
int row = word1.size(), col = word2.size();
vector<vector<int>> dp(row+1, vector<int>(col+1,0));
for(int i = 1; i <= row; i++) //从长度为 i 的字符串转为空串 要删除 i 次
dp[i][0] = i;
for(int j = 1; j <= col; j++) //从空串转为长度为 j 的字符串 要添加 j 次
dp[0][j] = j;
for(int i = 1; i <= row; i++){
for(int j = 1; j <= col; j++){
if(word1[i-1] == word2[j-1])
dp[i][j] = dp[i-1][j-1];
else
dp[i][j] = min(min(dp[i-1][j-1] + 1, dp[i-1][j] + 1),dp[i][j-1] + 1);
}
}
return dp[row][col];
}
};扩展:
(1)子串匹配
void cal_next(char *str, int *next, int len)
{
next[0] = -1;//next[0]初始化为-1,-1表示不存在相同的最大前缀和最大后缀
int k = -1;//k初始化为-1
for (int q = 1; q <= len-1; q++)
{
while (k > -1 && str[k + 1] != str[q])//如果下一个不同,那么k就变成next[k],注意next[k]是小于k的,无论k取任何值。
{
k = next[k];//往前回溯
}
if (str[k + 1] == str[q])//如果相同,k++
{
k = k + 1;
}
next[q] = k;//这个是把算的k的值(就是相同的最大前缀和最 大后缀长)赋给next[q]
}
}
int KMP(char *str, int slen, char *ptr, int plen)
{
int *next = new int[plen];
cal_next(ptr, next, plen);//计算next数组
int k = -1;
for (int i = 0; i < slen; i++)
{
while (k >-1&& ptr[k + 1] != str[i])//ptr和str不匹配,且k>-1(表示ptr和str有部分匹配)
k = next[k];//往前回溯
if (ptr[k + 1] == str[i])
k = k + 1;
if (k == plen-1)//说明k移动到ptr的最末端
{
//cout << "在位置" << i-plen+1<< endl;
//k = -1;//重新初始化,寻找下一个
//i = i - plen + 1;//i定位到该位置,外层for循环i++可以继续找下一个(这里默认存在两个匹配字符串可以部分重叠),感谢评论中同学指出错误。
return i-plen+1;//返回相应的位置
}
}
return -1;
}3. 最长公共子序列
假如S1的最后一个元素 与 S2的最后一个元素相等,那么S1和S2的LCS就等于 {S1减去最后一个元素} 与 {S2减去最后一个元素} 的 LCS 再加上 S1和S2相等的最后一个元素。
假如S1的最后一个元素 与 S2的最后一个元素不等,那么S1和S2的LCS就等于 : {S1减去最后一个元素} 与 S2 的LCS, {S2减去最后一个元素} 与 S1 的LCS 中的最大的那个序列。
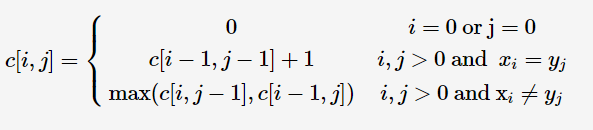
public static int lcs(String str1, String str2) {
int len1 = str1.length();
int len2 = str2.length();
int c[][] = new int[len1+1][len2+1];
for (int i = 0; i <= len1; i++) {
for( int j = 0; j <= len2; j++) {
if(i == 0 || j == 0) {
c[i][j] = 0;
} else if (str1.charAt(i-1) == str2.charAt(j-1)) {
c[i][j] = c[i-1][j-1] + 1;
} else {
c[i][j] = max(c[i - 1][j], c[i][j - 1]);
}
}
}
return c[len1][len2];
} 最长公共子串
public static int lcs(String str1, String str2) {
int len1 = str1.length();
int len2 = str2.length();
int result = 0; //记录最长公共子串长度
int c[][] = new int[len1+1][len2+1];
for (int i = 0; i <= len1; i++) {
for( int j = 0; j <= len2; j++) {
if(i == 0 || j == 0) {
c[i][j] = 0;
} else if (str1.charAt(i-1) == str2.charAt(j-1)) {
c[i][j] = c[i-1][j-1] + 1;
result = max(c[i][j], result);
} else {
c[i][j] = 0;
}
}
}
return result;
} 最长递增子序列
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
//O(n^2)
/*
vector dp(nums.size(), 1);
int res = 0;
for (int i = 0; i < nums.size(); ++i) {
for (int j = 0; j < i; ++j) {
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
res = max(res, dp[i]);
}
return res;
*/
//O(nlogn)
vector<int> dp;
for (int i = 0; i < nums.size(); ++i) {
int left = 0, right = dp.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (dp[mid] < nums[i]) left = mid + 1;
else right = mid;
}
if (right >= dp.size()) dp.push_back(nums[i]);
else dp[right] = nums[i];
}
return dp.size();
}
};最大连续子序列和
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
if(array.size() == 0)
return 0;
int res = array[0];
int curSum = array[0];
for(int i = 1;i<array.size();i++){
curSum = max(curSum + array[i],array[i]);
res = max(curSum,res);
}
return res;
}
};最大连续子序列乘积
访问到每个点的时候,以该点为子序列的末尾的乘积,要么是该点本身,要么是该点乘以以前一点为末尾的序列,注意乘积负负得正,故需要记录前面的最大最小值。
dp1[i]:以第i个数结尾的连续子序列最大乘积
dp2[i]:以第i个数结尾的连续子序列最小乘积
转移方程:
dp1[i]=max(data[i],dp1[i-1]*data[i],dp2[i-1]*data[i]);
dp2[i]=min(data[i],dp1[i-1]*data[i],dp2[i-1]*data[i]);
double func(double *a,const int n)
{
double *maxA = new double[n];
double *minA = new double[n];
maxA[0] = minA[0] =a[0];
double value = maxA[0];
for(int i = 1 ; i < n ; ++i)
{
maxA[i] = max(max(a[i],maxA[i-1]*a[i]),minA[i-1]*a[i]);
minA[i] = min(min(a[i],maxA[i-1]*a[i]),minA[i-1]*a[i]);
value=max(value,maxA[i]);
}
return value;
}