李宏毅机器学习：RNN（上）

以订票系统中的Slot Filling为例，我们希望订票系统听到用户说:”I would like to arrive  Taipei  on  November 2nd .” 时做好Slot Filling, 即识别出语音中 Taipei 属于 Destination 这个slot, November 2nd 属于 Time of arrival 这个slot, 而其它词汇不属于任何slot。 
能否用Feedforward network解决这一问题呢？ 
先说结论：不能。 

为什么呢？我们把word变成vector（e.g. 1-of-N encoding, word hashing）作为Feedforward network的输入，输出是该词汇属于slots(Destination, Time of arrival) 的概率。但是这样是不够的，因为在slot filling的任务中，neural network是需要有记忆的，要记住在Taipei之前出现过的arrive或leave。这种有记忆的neural network叫做Recurrent Neural Network. 

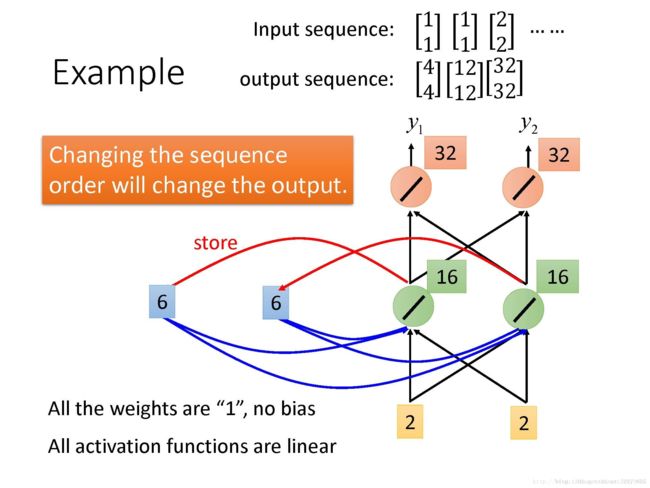
在RNN中，hidden layer的neuron产生的output会被存到memory中，对之后的input, hidden layer的neuron不只考虑input， 还会考虑存在memory中的值。memory在没有任何input时需要初始值。 

RNN会考虑input sequence的order，改变input sequence的order，output会随之改变。 

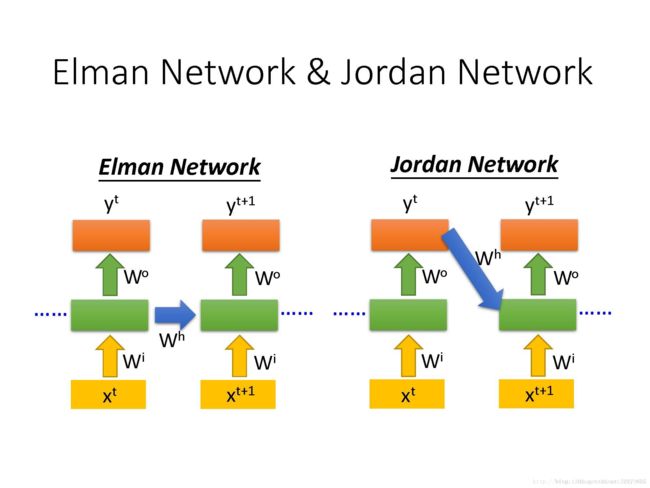
RNN有不同的变形，Elman Network & Jordan Network. 

据说 Jordan Network 有更好的performance，因为在Elman Network 中放到memory里的是没有target的，有点难控制它学到什么东西放到memory里面，而在Jordan Network中放到memory里的是有target的，我们比较清楚放到target中的是什么东西。

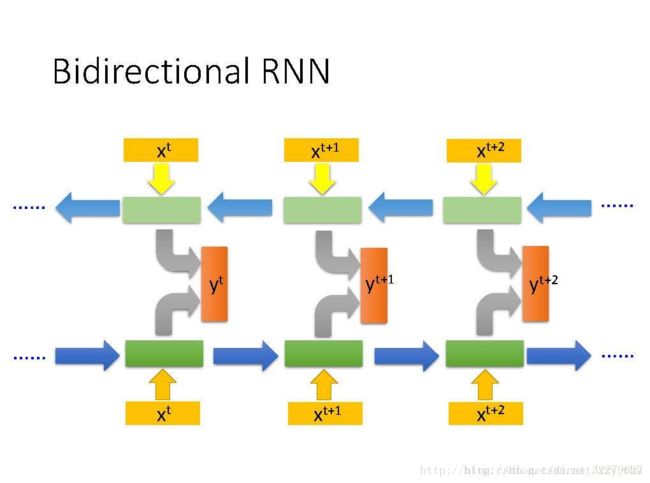
RNN还可以是双向的。刚才看到的例子中，输入一个句子，RNN从句首读到句尾。其实读的顺序也可以是反过来的。同时训练正向RNN与逆向RNN，将二者的hidden layer都接给一个output layer。用双向RNN的好处是，它产生output时看的范围比较广，看了整个input sequence。 

LSTM的基本概念与内部结构

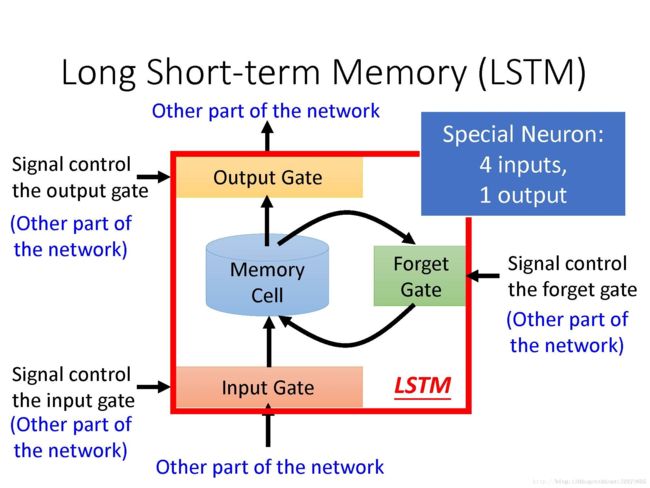
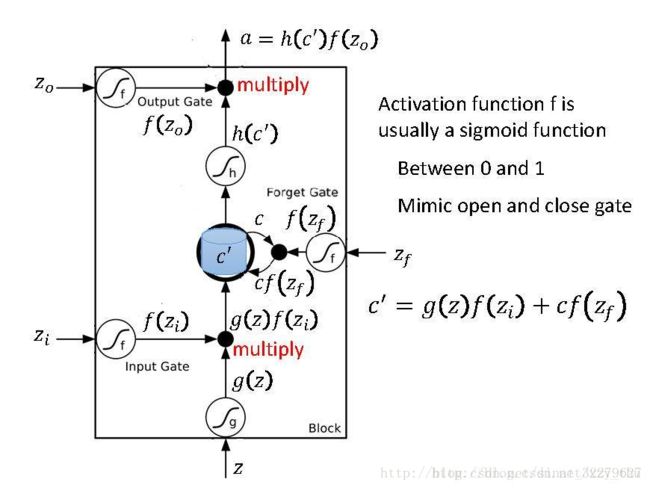
现在常用的memory是LSTM(Long Short-Term Memory), 结构比较复杂，有三个Gate. 
当外界想写入memory cell的时候，必须通过input gate，只有在input gate被打开的时候，memory gate才可以被写入，input gate 是打开还是关闭，是neural network自己学的。同理还有一个output gate, 它的开或关也是neural network 学到的。还有一个forget gate, 决定什么时候将memory cell中的内容忘掉，它的开或关也是neural network 学到的。 
可以将LSTM看做special neuron(4 inputs, 1 output), 4 inputs指的是外界想要存到memory cell 里的值+控制三个门的信号。

顺便一提，Long Short-term Memory 里的Long 是形容Short-term Memory 的。在最开始看到的最简单的RNN模型中，memory是short-term的，每次有新的输入，memory都会被洗掉。而LSTM的short-term比较long: 只要控制forget gate的信号决定不forget，memory的值就会被存起来。

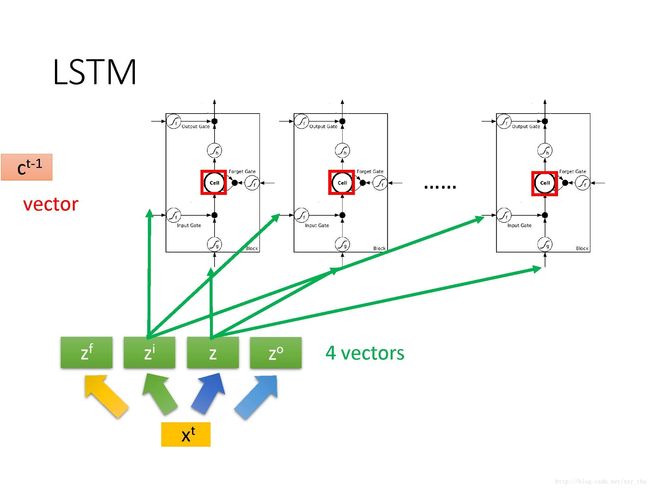
下面这张图更清晰的表现了LSTM的结构，z,zi,zo,zfz,zi,zo,zf 都是scalar, 这4个input scalar 是由input vector与weight vector计算内积再加上bias而来，weight vector与bias是由training data用gradient descent学到的。 
函数ff 常选sigmoid，因为sigmoid输出的0-1之间的值可以表示gate打开的程度（1：打开，0：关闭）。f(zi)=1 时，允许输入； f(zi)=0时，相当于无输入。f(zo)=1 时，允许输出；f(zi)=0时，相当于无法输出。f(zf)=1时，相当于记得memory cell中之前的值c；f(zf)=0时，相当于洗掉 
c 。 
memory cell中的值按图中的公式进行更新。 

LSTM组成的网络

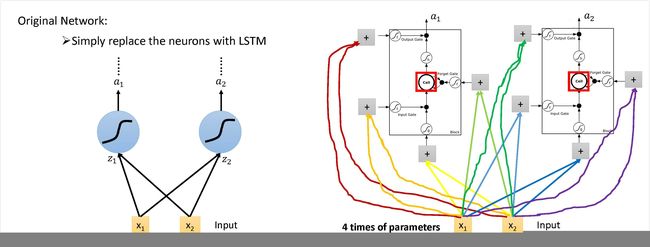
把之前的网络中的neuron换成LSTM，就是用LSTM的网络的结构。参数量变成了之前的4倍。 

假设现在一层有n个LSTM，n个memory cell的值组成vector  ct−1 , 下图中的 z,zi,zf,zoz, 都是n维vector, 第i维控制第i个LSTM相应的gate。 

而实际中要更复杂一点：把每个LSTM在时刻t的output ht接到该LSTM在下一时刻的输入，同时所谓peephole的意思是把前一时刻memory cell中的值也拉到下一时刻的input中。即，操控LSTM4个input z,zi,zf,zoz,时同时考虑了xt+1,ht,ctx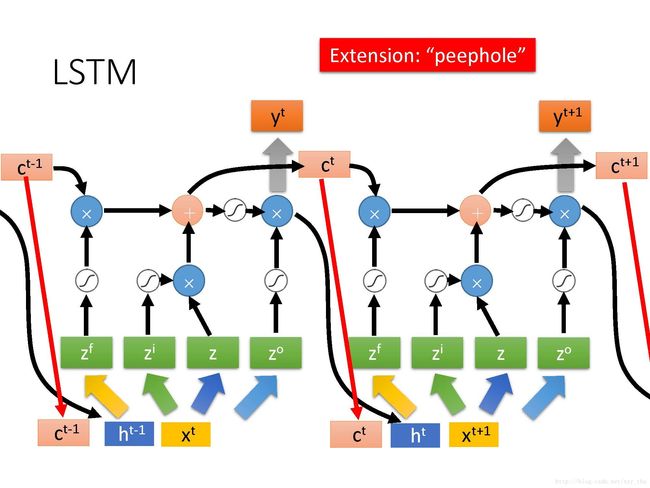

一般一层不够，所谓Multiple-layer LSTM就是把前一层各LSTM输出的ht作为下一层对应LSTM的输入xt.

Keras支持三种RNN，分别是LSTM, GRU（LSTM的简化，只有两个gate，减少了参数避免了过拟合，performance与LSTM差不多）, SimpleRNN（本节最开始的RNN结构）。