因子分析、主成分分析（PCA）、独立成分分析（ICA）——斯坦福CS229机器学习个人总结（六）

因子分析是一种数据简化技术，是一种数据的降维方法。
因子分子可以从原始高维数据中，挖掘出仍然能表现众多原始变量主要信息的低维数据。此低维数据可以通过高斯分布、线性变换、误差扰动生成原始数据。
因子分析基于一种概率模型，使用EM算法来估计参数。

主成分分析（PCA）也是一种特征降维的方法。
学习理论中，特征选择是要剔除与标签无关的特征，比如“汽车的颜色”与“汽车的速度”无关；
PCA中要处理与标签有关、但是存在噪声或者冗余的特征，比如在一个汽车样本中，“千米/小时”与“英里/小时”中有一个冗余了。
PCA的方法比较直接，只要计算特征向量就可以降维了。

独立成分分析（ICA）是一种主元分解的方法。
其基本思想是从一组混合的观测信号中分离出独立信号。比如在一个大房间里，很多人同时在说话，样本是这个房间里各个位置的一段录音，ICA可以从这些混合的录音中分离出每个人独立的说话的声音。
ICA认为观测信号是若干个统计独立的分量的线性组合，ICA要做的是一个解混过程。

因为因子分析、PCA、ICA都是对数据的处理方法，就放在这同一份总结里了。

1、因子分析（Factor analysis）

1.1、因子分析的直观理解

因子分析认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的。让我们来看一个简单例子，对低维数据如何生成高维数据有一个直观理解。

假设我们有m=5个2维原始样本点如下：

图一

那么按照因子分析的做法，原始数据可以由以下过程生成：
①在一个低维空间（此处是1维）中，存在着由高斯分布生成的 m 个点 z(i) ， z(i) ~ N(0,I) ：

图二
②使用某个 Λ=(a,bT) 将1维的 z 映射到2维的空间中：

图三
③加上 μ(μ1,μ2)T ，让直线过 μ ——实际上是将样本点横坐标加 μ1 ，纵坐标加 μ2 ：

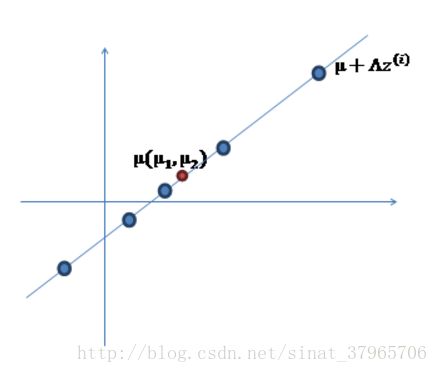
图四
④对直线上的点做一定的扰动，其扰动为 ε ~ N(0,ψ) ：

图五
黑点就是图一中的原始数据。

1.2、因子分析的一般过程

因子分析认为m个n维特征的训练样例 (x(1),x(2),⋯,x(m)) 的产生过程如下：
①在一个 k 维空间中，按照多元高斯分布生成m个 z(i) （ k 维向量， k<n ），即
z(i) ~ N(0,I)
②存在一个变换矩阵 Λ∈Rn∗k ，将 z(i) 映射到 n 维空间中，即
Λz(i)
③将 Λz(i) （ n 维）加上一个均值 μ （ n 维），即
μ+Λz(i)
④对每个点加上符合多元高斯分布的扰动 ε ~ N(0,ψ) （ n 维向量），即
x(i)=μ+Λz(i)+ε

1.3、因子分析模型

模型与参数概述

由上面的分析，我们定义因子分析的模型为：

z ~ N(0,I)
ε ~ N(0,ψ)
x=μ+Λz+ε(1)
其中 z 和 ε 是相互独立的。并且由上面的分析过程，我们可以直观地感受到我们的 参数是 μ∈Rn 、 Λ∈Rn∗k 、 ψ∈Rn∗n 。

另一个等价的假设是， (x,z) 联合分布如下，其中 z∈Rk 是一个隐藏随机变量：

x∣z ~ N(μ+Λz,ψ) (2)
这个假设会在使用EM算法求解因子分析参数，E步中迭代 Q 分布的时候用到。

接下来的课程，是使用高斯模型的矩阵表示法来对模型进行分析。矩阵表示法认为 z 与 x 联合符合多元高斯分布，即：

[zx] ~ N(μzx,Σ)
多元高斯分布的原始模型是：

f(x)=12πk|Σ|−−−−−−√exp(−12(x−μ)TΣ−1(x−μ))(3)

其中 x 是 k 维向量， μ 是 k 维向量， Σ 是 k∗k 协方差矩阵。
很明显在多元高斯分布模型下，参数是 μzx,Σ ——它们是由 x,z 的联合分布生成的，所以我们可以用我们的原始参数 μ,Λ,ψ 来表示 μzx,Σ ，求得 x 的边缘分布，再把相关参数带入式（3），这就得到了关于我们参数的概率分布，然后就可以通过最大似然估计来求取我们的参数。

求取 μzx

μzx 是 x,z 联合分布的期望值（期望的定义：所有结果*相应概率的总和）：

μzx=E[zx]=[E(z)E(x)](4)

由 z ~ N(0,I) 我们可以简单获得 E(z)=0 。
类似地由 ε ~ N(0,ψ) ， x=μ+Λz+ε ， μ 是一个常数，我们有：

E[x]=E[μ+Λz+ε]=E[μ]+ΛE[z]+E[ε]=μ+0+0=μ(5)

所以：

μzx=[0⃗ μ](6)

求取 Σ

Σ 是 x,z 联合分布的协方差矩阵。
方差，度量随机变量与期望之间的偏离程度，定义如下：

Var(X)=E((X−E(X))2)=E(X2)−(E(X)2)(7)

协方差，两个变量总体误差的期望，定义如下：

Cov(X,Y)=E((X−E(X))(Y−E(Y)))(8)

协方差、方差、期望之间的一些相互关系如下：

Cov(X,X)=Cov(X)=Var(X)=E(XXT)=σ2(9)

下面开始求取 Σ 。

Σ=Cov[zx]=[ΣzzΣxzΣzxΣxx]=E[(z−E(z))(z−E(z))T(x−E(x))(z−E(z))T(z−E(z))(x−E(x))T(x−E(x))(x−E(x))T](10)

由 z ~ N(0,I) ，可以简单得到：

Σzz=Cov(z)=σ2=I(11)

由 ε ~ N(0,ψ) ， x=μ+Λz+ε ， E(x)=μ ，并且 z 和 ε 是相互独立，有：

Σzx=E[(z−E(z))(x−E(x))T]=E[(z−0)(μ+Λz+ε−μ)T]=E[zzT]ΛT+E[zεT]=IΛT+0=ΛT(12)

类似地，我们可以得到：

Σxx=E[(x−E(x))(x−E(x))T]=E[(μ+Λz+ε−μ)(μ+Λz+ε−μ)T]=ΛE[zzT]ΛT+E[εεT]=ΛIΛT+ψ=ΛΛT+ψ(13)

用最大似然估计法求解参数

经过上面的步骤，我们就把 μzx,Σ 用我们的参数 μ,Λ,ψ 表示出来了：

[zx] ~ N(μzx,Σ) ~ N([0⃗ μ],[IΛΛTΛΛT+ψ])
然后我们可以求得 x 的边缘分布：
x ~ N(μ,ΛΛT+ψ)
因此，给定一个训练集 {x(i);i=1,2,⋯,m} ，把参数带入式（3），我们可以写出下面的似然函数：

l(μ,Λ,ψ)=log∏i=1m12πn∣∣ΛΛT+ψ∣∣−−−−−−−−−−−√exp(−12(x(i)−μ)T(ΛΛT+ψ)−1(x(i)−μ))(14)

对此似然函数做最大似然估计，就能求得我们的参数。

1.4、因子分析的EM求解

可以感受到，直接对这个似然函数求解是很困难的，在这个情况下，用EM算法就登场了——当一个似然函数难以直接求解其最大值的时候，可以通过EM算法不断建立下界、最大化下界的方式不断逼近该似然函数真实的最大值，当EM算法收敛，我们就认为已经求得了此最大值。

E-step

对于EM算法的E-step，我们有：

Qi(z(i)):=p(z(i)∣x(i);μ,Λ,ψ)(15)

进一步地：

Qi(z(i))=12πk∣∣Σz(i)∣x(i)∣∣−−−−−−−−−−√exp(−12(z(i)−μz(i)∣x(i))TΣ−1z(i)∣x(i)(z(i)−μz(i)∣x(i)))(16)

其中：

μz(i)∣x(i)Σz(i)∣x(i)=ΛT(ΛΛT+ψ)−1(x(i)−μ)=I−ΛT(ΛΛT+ψ)−1Λ(17)

μz(i)∣x(i),Σz(i)∣x(i) 是讲义与课上直接给出的，这里也不进行推导。

M-step

在M-step中，我们需要最大化如下公式来求取参数 μ,Λ,ψ ：

∑i=1m∫z(i)Qi(z(i))logp(x(i),z(i);μ,Λ,ψ)Qi(z(i))dz(i)(18)

视为期望，打开log

在这里，因为 z 是连续的，所以使用积分；如果是离散的，则使用累加。
并且，积分部分可以当成 z 服从 Q 分布时，函数 logp(x(i),z(i);μ,Λ,ψ)Qi(z(i)) 的期望，这里将会用E表示，省略 z(i) ~ Qi 的下标；对于函数中 x,z 的联合分布，我们可以用贝叶斯公式把它打开 p(x,z)=p(x∣x)p(z) ；为了方便计算我们还要把log函数打开——经过这些分析，我们有如下推导：

∑i=1m∫z(i)Qi(z(i))logp(x(i),z(i);μ,Λ,ψ)Qi(z(i))dz(i)=∑i=1mE[logp(x(i),z(i);μ,Λ,ψ)Qi(z(i))]=∑i=1mE[logp(x(i)∣z(i);μ,Λ,ψ)p(z(i))Qi(z(i))]=∑i=1mE[logp(x(i)∣z(i);μ,Λ,ψ)+logp(z(i))−logQi(z(i))](19)

去掉无关项后带入具体分布

这就比较清爽了，然后，记住我们的目标是求得参数 μ,Λ,ψ ，但是它们不能一起求解，所以下面以参数 Λ 为例，对公式进行求解——在式（19）中，对参数 Λ 求偏导。另外式（19）中的 p(z(i) 与 Qi(z(i)) 与 Λ 无关，可以忽略掉，所以实际上就是对下式求偏导：

∑i=1mE[logp(x(i)∣z(i);μ,Λ,ψ)](20)

在对式（20）求偏导之前，还可以对其进行一些处理——由式（2），并且 x∣z 服从多元高斯分布，所以有：

∑i=1mE[logp(x(i)∣z(i);μ,Λ,ψ)]=∑i=1mE[log12πn|ψ|−−−−−−√exp(−12(x(i)−(μ+Λz(i)))Tψ−1(x(i)−(μ+Λz(i))))]=∑i=1mE[−12log|ψ|−n2log(2π)−12(x(i)−μ−Λz(i))Tψ−1(x(i)−μ−Λz(i)))](21)

去掉无关项后求偏导

同样地，我们的目标是与 Λ 有关的项，所以忽略掉前面的无关项之后，我们实际上是对下式求偏导并求解：

∇Λ∑i=1mE[−12(x(i)−μ−Λz(i))Tψ−1(x(i)−μ−Λz(i)))]=∑i=1m∇Λ−E[12((x(i)T−μT)ψ−1A−z(i)TΛTψ−1B)((x(i)−μ)C−Λz(i)D)]=∑i=1m∇Λ−E[12(AC−AD−BC+BD)](22)

打开后我们可以发现， AC 这一项是与 Λ 无关的，把这一项忽略掉，所以由式（22）继续推导有：

∑i=1m∇Λ−E[12(−AD−BC+BD)]=∑i=1m∇Λ−E[12(−(x(i)T−μT)ψ−1Λz(i)E−z(i)TΛTψ−1(x(i)−μ)F+z(i)TΛTψ−1Λz(i))](23)

因为期望是一个常数，又因为 a=tr(a) ，所以可以直接对上式求迹；
因为 trA=trAT ，可以对E求转置，又因为对角矩阵的转置是它本身—— (ψ−1)T=ψ−1 ，所以有 trE=trET=trF ，对式（23）继续推导有：

∑i=1m∇Λ−E[12(−(x(i)T−μT)ψ−1Λz(i)E−z(i)TΛTψ−1(x(i)−μ)F+z(i)TΛTψ−1Λz(i))]=∑i=1m∇Λ−E[tr12(−z(i)TΛTψ−1(x(i)−μ)ET−z(i)TΛTψ−1(x(i)−μ)F+z(i)TΛTψ−1Λz(i))]=∑i=1m∇ΛE[−tr12z(i)TΛTψ−1Λz(i)+trz(i)TΛTψ−1(x(i)−μ)](24)

然后利用 trAB=trBA ，把式（25）中的 z(i)T 放到它们自己的后面，再把求导切换到期望里面——求导是针对 Λ ，期望是针对 z(i) ，所以是可以切换的：

∑i=1m∇ΛE[−tr12z(i)TΛTψ−1Λz(i)+trz(i)TΛTψ−1(x(i)−μ)]=∑i=1m∇ΛE[−tr12ΛTψ−1Λz(i)z(i)T+trΛTψ−1(x(i)−μ)z(i)T]=∑i=1m(E[−∇Λtr12ΛTψ−1Λz(i)z(i)T]+E[∇ΛtrΛTψ−1(x(i)−μ)z(i)T])(25)

对于式（25），先用矩阵的迹的性质 ∇ATf(A)=(∇Af(A))T 处理一下：

∑i=1m(E[−(∇ΛTtr12ΛTψ−1Λz(i)z(i)T)T]+E[(∇ΛTtrΛTψ−1(x(i)−μ)z(i)T)T])(26)

对式（26）的第一项使用 ∇AtrABATC=CAB+CTABT 的性质，对第二项使用 ∇AtrAB=BT 的性质：

∑i=1m⎛⎝⎜⎜E⎡⎣⎢⎢−⎛⎝⎜∇ΛTAtr12ΛTAψ−1BΛATz(i)z(i)TC⎞⎠⎟T⎤⎦⎥⎥+E⎡⎣⎢⎢⎛⎝⎜∇ΛTAtrΛTAψ−1(x(i)−μ)z(i)TB⎞⎠⎟T⎤⎦⎥⎥⎞⎠⎟⎟=∑i=1mE((−12z(i)z(i)TΛTψ−1−12(z(i)z(i)T)TΛT(ψ−1)T)T+((ψ−1(x(i)−μ)z(i)T)T)T)=∑i=1mE((−z(i)z(i)TΛTψ−1)T+ψ−1(x(i)−μ)z(i)T)=∑i=1mE(−ψ−1Λz(i)z(i)T+ψ−1(x(i)−μ)z(i)T)(27)

令式（27）=0，并化简，就可以求得参数 Λ ：

⟹⟹⟹∑i=1mE(−ψ−1Λz(i)z(i)T+ψ−1(x(i)−μ)z(i)T)=0∑i=1m−ψ−1ΛE[z(i)z(i)T]+∑i=1m−ψ−1(x(i)−μ)E[z(i)T]=0∑i=1mΛE[z(i)z(i)T]=∑i=1m(x(i)−μ)E[z(i)T]Λ=(∑i=1m(x(i)−μ)E[z(i)T])(∑i=1mE[z(i)z(i)T])−1(28)

我们发现，这里的公式与线性回归中最小二乘法的矩阵形式相似。
相似原因：在因子分析中， x 是 z 的线性函数，在E-step中给出 z 的 Q 分布之后，在M-tep中寻找 x 与 z 的映射关系 Λ ；在线性回归的最小二乘中，也是寻找 x 与 y 的线性关系。
不同之处：最小二乘只用到了 z 的最优估计，因子分析还用到了 z(i)z(i)T 的估计。

对于参数 Λ ，这里还有未知数 E[z(i)T] 与 E[z(i)z(i)T] ，并且此处的期望是在 z(i) 服从 Qi 前提下计算的，所以对于前者，通过式（17）我们有：

E[z(i)T]=μTz(i)∣x(i)(29)

对于后者，由式（7）~式（9）方差与协方差的性质，我们有：

Cov(z)⟹E[z(i)z(i)T]=E(zzT)−E(z)E(zT)=E(z(i))E(z(i)T)+Cov(z)=μz(i)∣x(i)μTz(i)∣x(i)+Σz(i)∣x(i)(30)

注意这里的 E[z(i)z(i)T] 不仅仅等于 E(z(i))E(z(i)T) ，后面还有加上一个后验概率 p(z∣x) 协方差，要特别注意。

到这里，我们就可以把参数 Λ 的最终形式给出来了：

Λ=(∑i=1m(x(i)−μ)μTz(i)∣x(i))(∑i=1m