python——pandas数据分析(表格处理)工具实现Apriori算法

pandas 是基于NumPy 的一种工具， 名字很卡哇伊，来源是由“ Panel data”（面板数据，一个计量经济学名词）两个单词拼成的。pandas纳入了大量库和一些标准的数据模型，提供了高效地操作大型数据集所需的工具。主要应用于处理大型数据集。数据处理速度算是最大的特色，剩下的就是个python版的excel了吧。

API文档：http://pandas.pydata.org/pandas-docs/stable/user_guide/visualization.html

数据结构:

Series：一种一维数组，和 NumPy 里的数组很相似。事实上，Series 基本上就是基于 NumPy 的数组对象来的。和 NumPy 的数组不同，Series 能为数据自定义标签，也就是索引（index），然后通过索引来访问数组中的数据。

DataFrame：二维的表格型数据结构。很多功能与R中的data.frame类似。可以将DataFrame理解为Series的容器。

Panel ：三维的数组，可以理解为DataFrame的容器。

例如：

import numpy as np 
import pandas as pd

datafile='.\opt\list.csv'
outfile='.\opt\output.csv'
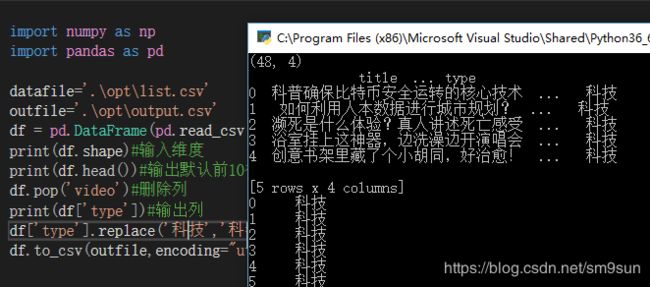
df = pd.DataFrame(pd.read_csv(datafile,encoding="utf_8"))#导入文件
print(df.shape)#输入维度
print(df.head())#输出默认前10行
df.pop('video')#删除列
print(df['type'])#输出列
df['type'].replace('科技','科学',inplace = True)#列替换
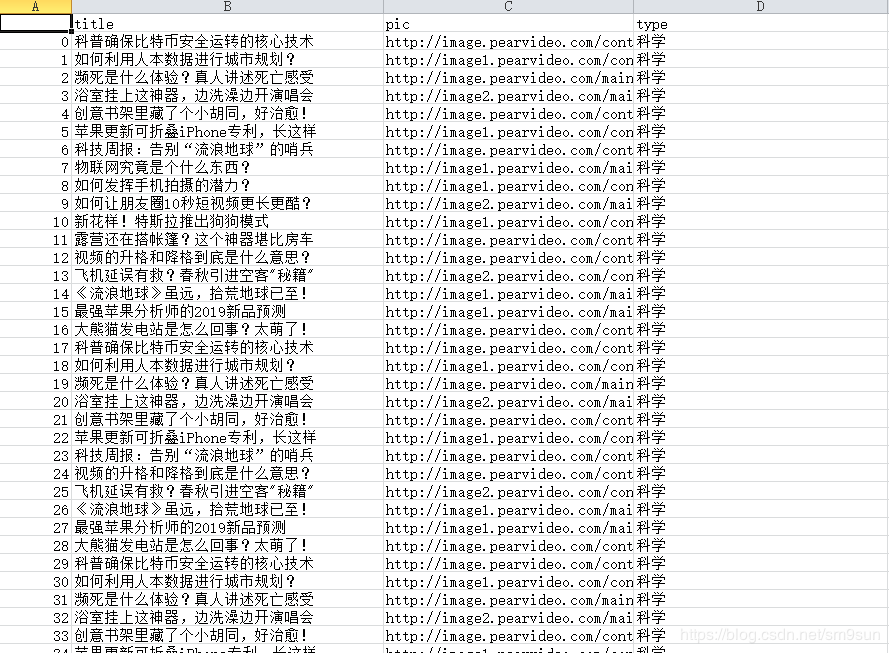
df.to_csv(outfile,encoding="utf_8")#输出文件

list.csv：

output.csv：

 

 

下面介绍Apriori算法：

Apriori算法是常用的用于挖掘出数据关联规则的算法，算法的目标是找到最大的K项频繁集，采用了迭代的方法，先搜索出候选1项集及对应的支持度，剪枝去掉低于支持度的1项集，得到频繁1项集。然后对剩下的频繁1项集进行连接，得到候选的频繁2项集，筛选去掉低于支持度的候选频繁2项集，得到真正的频繁二项集，以此类推，迭代下去，直到无法找到频繁k+1项集为止，对应的频繁k项集的集合即为算法的输出结果。

算法流程：

1）扫描整个数据集，得到所有出现过的数据，作为候选频繁1项集。k=1，频繁0项集为空集。

2）挖掘频繁k项集

    a) 扫描数据计算候选频繁k项集的支持度

    b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空，则直接返回频繁k-1项集的集合作为算法结果，算法结束。如果得到的频繁k项集只有一项，则直接返回频繁k项集的集合作为算法结果，算法结束。

    c) 基于频繁k项集，连接生成候选频繁k+1项集。

3） 令k=k+1，转入步骤2。

参考代码https://spaces.ac.cn/archives/3380

#-*- coding: utf-8 -*-
from __future__ import print_function
import pandas as pd

d = pd.read_csv('./opt/test.csv',header=None, dtype = object)

print(u'\n转换原始数据至0-1矩阵...')
import time
start = time.clock()
ct = lambda x : pd.Series(1, index = x)
b = map(ct, d.values)
d = pd.DataFrame(list(b)).fillna(0)
d = (d==1)
end = time.clock()
print(u'\n转换完毕，用时：%0.2f秒' %(end-start))
print(u'\n开始搜索关联规则...')
del b

support = 0.06 #最小支持度
confidence = 0.75 #最小置信度
ms = '--' #连接符，用来区分不同元素，如A--B。需要保证原始表格中不含有该字符

#自定义连接函数，用于实现L_{k-1}到C_k的连接
def connect_string(x, ms):
    x = list(map(lambda i:sorted(i.split(ms)), x))
    l = len(x[0])
    r = []
    for i in range(len(x)):
        for j in range(i,len(x)):
            if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
                r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
    return r

#寻找关联规则的函数
def find_rule(d, support, confidence):
    import time
    start = time.clock()
    result = pd.DataFrame(index=['support', 'confidence']) #定义输出结果

    support_series = 1.0*d.sum()/len(d) #支持度序列
    column = list(support_series[support_series > support].index) #初步根据支持度筛选
    k = 0

    while len(column) > 1:
        k = k+1
        print(u'\n正在进行第%s次搜索...' %k)
        column = connect_string(column, ms)
        print(u'数目：%s...' %len(column))
        sf = lambda i: d[i].prod(axis=1, numeric_only = True) #新一批支持度的计算函数

        #创建连接数据，这一步耗时、耗内存最严重。当数据集较大时，可以考虑并行运算优化。
        d_2 = pd.DataFrame(list(map(sf,column)), index = [ms.join(i) for i in column]).T

        support_series_2 = 1.0*d_2[[ms.join(i) for i in column]].sum()/len(d) #计算连接后的支持度
        column = list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
        support_series = support_series.append(support_series_2)
        column2 = []
        
        for i in column: #遍历可能的推理，如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B？
            i = i.split(ms)
            for j in range(len(i)):
                column2.append(i[:j]+i[j+1:]+i[j:j+1])
        
        cofidence_series = pd.Series(index=[ms.join(i) for i in column2]) #定义置信度序列
        
        for i in column2: #计算置信度序列
            cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
        
        for i in cofidence_series[cofidence_series > confidence].index: #置信度筛选
            result[i] = 0.0
            result[i]['confidence'] = cofidence_series[i]
            result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]

    result = result.T.sort_values(['confidence','support'], ascending = False) #结果整理，输出
    end = time.clock()
    print(u'\n搜索完成，用时：%0.2f秒' %(end-start))
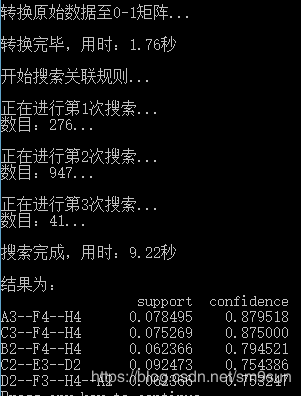
    print(u'\n结果为：')
    print(result)
    
    return result

find_rule(d, support, confidence).to_csv('./opt/out.csv')

测试文本：https://spaces.ac.cn/usr/uploads/2015/07/3424358296.txt

推荐参考博客：

https://www.jianshu.com/p/a77b0bc736f2

https://www.cnblogs.com/pinard/p/6293298.html

https://spaces.ac.cn/archives/3380