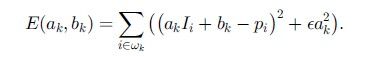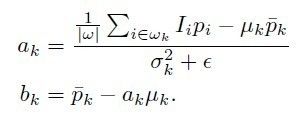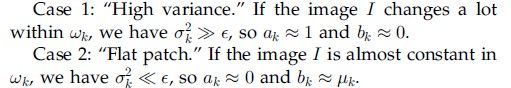保持边缘的滤波函数————Guided Image Filtering

1，定义

引导滤波：即需要引导图的滤波器，引导图可以是单独的图像或者是输入图像，当引导图为输入图像时，引导滤波就成为一个保持边缘的滤波操作，可以用于图像重建的滤波。

引导滤波的流程见下图：

假设输入图像为p，输出图像为q，引导图为I，q与I在以像素k为中心的窗口中存在局部线性关系：

窗口半径为r，a，b为线性系数，且在局部窗口k中为常数。这个模型保证了只有在I存在边缘的情况下，q才会存在边缘。这是因为：。这与在去雾、超分辨率、抠图等研究中使用的模型是一致的。

q即p去除噪声或者纹理之后的图像：

为确定以上公式中的线性系数，并满足使得q与p的差别最小，转化为最优化问题：

以上公式的求解可以利用线性回归：

在这里, μk和σk^2表示I在局部窗口wk中的均值和方差。 |ω|是窗口内的像素数，pk表示p在窗口wk中的均值。当求的ak和bk后：

其中,

，

算法流程：f为一个窗口半径为r的均值滤波器，corr为相关，var为方差，cov为协方差。

2，边缘保持

当I=P时，引导滤波就变成了边缘保持的滤波操作，此时：

，

考虑两种情况：

 

即在高方差区域，保持值不变，在平滑区域，使用临近像素平均。

3，彩色滤波

直观的方法就是直接将引导滤波应用到三个颜色通道中（RGB）：

 

 取值：i=1，2，3

4，简单示例

下载作者代码后，有两个主要函数：guidedfilter.m（灰度图像）和guidedfilter_color.m（彩色图像），随便取一副图像进行边缘保持滤波：

I = double(imread('.\img_smoothing\cat.bmp')) / 255;

p = I;

r = 4; % try r=2, 4, or 8

eps = 0.2^2; % try eps=0.1^2, 0.2^2, 0.4^2

 

q = guidedfilter(I, p, r, eps);

 

figure();

imshow([I, q], [0, 1]);

结果图：

5，一些资源

项目主页：http://research.microsoft.com/en-us/um/people/kahe/eccv10/index.html

 

http://blog.csdn.net/kaikaicheng/article/details/8108474

同时作者提供了代码和ppt可供参考，也可从博主资源中下载。

http://download.csdn.net/detail/u010736419/6840011

http://download.csdn.net/detail/u010736419/6840015

http://download.csdn.net/detail/u010736419/6840025

 

相关论文：

• Guided Image Filtering, by Kaiming He, Jian Sun, and Xiaoou Tang, in ECCV 2010 (Oral).
• Guided Image Filtering, by Kaiming He, Jian Sun, and Xiaoou Tang, in TPAMI 2013.
• Constant Time Weighted Median Filtering for Stereo Matching and Beyond, by Ziyang Ma, Kaiming He, Yichen Wei, Jian Sun, and Enhua Wu, inICCV 2013.
•