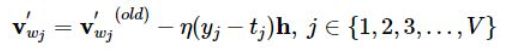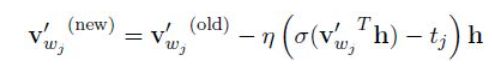word2vec原理总结
Part I:背景
Part II:训练模式(CBOW,Skip Gram)
Part III:优化方法(Negative Sampling,Hierarchical SoftMax)
Part IV:词向量衡量指标
参考论文:Word2vec Parameter Learning Explained
Part I:背景
特征表达是很基础也很重要的一步,我们通常需要用一个向量去表示一个东西,比如文本中的词向量,知识图谱中的知识向量,以及Network Embedding等。
在NLP中,传统算法通常使用one-hot形式表示一个词,存在以下问题:
1)维度爆炸,词表通常会非常大,导致词向量维度也会非常大。
2)损失语义信息,one hot随机给每个词语进行编号映射,无法表示词语之间的关系。
所以word embeding的优势如下:
1)将词语映射成一个固定维度的向量,节省空间。
2)词向量可能会具备一定的语义信息,将相似的词语放到相近的向量空间(比如香蕉和苹果都是属于水果,苹果又会涉及到歧义问题),可以学习到词语之间的关系(比如经典的 男人-女人=国王-王后)。
本文会介绍一下Word2vec原理,这是一种常见的可以用于训练词向量的模型工具。常见的做法是,我们先用word2vec在公开数据集上预训练词向量,加载到自己的模型中,对词向量进行调整,调整成适合自己数据集的词向量。
Part II:训练模式
我们通常是通过将词向量用于某些任务中,用这些任务的衡量指标去衡量模型结果。
那么反过来,如果我们想要训练词向量,可以先去训练一个语言模型,然后将模型中对应的参数,作为词向量。从任务形式上看,我们是在训练语言模型,而实际上我们最终的目标是想得到词向量,我们更关心的是这个词向量合不合理。
Word2vec根据上下文之间的出现关系去训练词向量,有两种训练模式,Skip Gram和CBOW,其中Skip Gram根据目标单词预测上下文,CBOW根据上下文预测目标单词,最后使用模型的部分参数作为词向量。
AutoEncoder也可以用于训练词向量,先将one hot映射成一个hidden state,再映射回原来的维度,令输入等于输出,取中间的hidden vector作为词向量,在不损耗原表达能力的前提下压缩向量维度,得到一个压缩的向量表达形式。
一. CBOW
根据上下文预测目标单词,我们需要极大化这个目标单词的出现概率。
假设词表大小为V,词向量维度为N,上下文单词为x1,x2, ..., xc,定义上下文窗口大小为c,对应的目标单词为y,我们将x跟y都表示成one hot形式。这里涉及到两个矩阵参数,W是词向量矩阵,每一行都是某个词的词向量v,W'可以看做是一个辅助矩阵,每一列可以看做是某个词对应的相关向量v'。
前向过程:
x->hidden:对于每个xi,取出对应的词向量vi,再对这些词向量取平均作为hidden vector,相当于通过简单粗暴的叠加,得到这些词语的语义向量。
h->y:将h乘以W'得到一个维度为V的向量u,进行softmax归一化得到概率向量,取概率最大的作为预测单词。
后向过程:
我们需要极大化目标单词的出现概率p(y | x1, x2, ... , xc),也就是极小化负对数似然函数,Loss函数定义为:
我们需要更新两个矩阵参数,W和W',先根据loss对参数求梯度,再使用梯度下降法更新参数。具体的求导过程这里略过,请移步原论文。
对于W',经过求导,v'更新公式为:
也就是说,需要更新整个W'矩阵,所有v'向量。(这里造成了巨大的计算量)
对于W,经过求导,v更新公式为:
也就是说,这里只需要更新c个上下文单词所对应的词向量。
二. Skip Gram
根据目标单词预测其上下文,假设输入的目标单词为x,定义上下文窗口大小为c,对应的上下文为y1, y2, ... , yc,这些y是相互独立的。
前向过程:
x->hidden:将输入单词x乘以词向量矩阵W,相当于取出该词的词向量v。
h->y:对于每个输出单词y_i,将h乘以矩阵W'得到向量u,再经过softmax归一化得到概率向量,取概率最大的预测为上下文单词,极大化y_i的预测概率。
这些上下文单词是相互独立的,虽然他们共享W',但是loss是不一样的,我们需要极大化这些词出现的概率。作为一个语言模型这种做法是略显粗糙,但是这里我们的目的只是为了训练词向量,并不是需要训练一个多么好的语言模型。
后向过程:
直观上的样本格式是(x,y1, y2, ... , yc),然后极大化p(y|x),因为这些y是相互独立的,又变成极大化p(y1|x)*p(y2|x)*...*p(yc|x),取log将连乘变成连加,取负将极大化变成极小化,使用交叉熵作为loss函数:
所以这里我们可以将样本格式定义成(x, y),将所有样本的Loss加起来。
对于W',经过求导,v'更新公式为:
也就是说,这里依然需要更新所有v'向量。(无法避免的巨大的计算量)
对于W,经过求导,v更新公式为:
这里只需要更新目标词语所对应的那个词向量。
Part III:优化方法
原始的方法所存在的问题是计算量太大,体现在以下两方面:
1)前向过程,h->y这部分在对向量进行softmax的时候,需要计算V次。
2)后向过程,softmax涉及到了V列向量,所以也需要更新V个向量。
问题就出在V太大,而softmax需要进行V次操作,用整个W进行计算。
因此word2vec使用了两种优化方法,Hierarchical SoftMax和Negative Sampling,对softmax进行优化,不去计算整个W,大大提高了训练速度。
一. Hierarchical SoftMax
HS用哈夫曼树,把预测one-hot编码改成预测一组01编码,进行层次分类。
在哈夫曼树中,每个叶节点是词表中的一个词,每个非叶子节点对应一个v'向量,树的深度为L(w),整颗树有V-1个非叶子节点和V个叶节点。假设输入单词是w_i,目标单词是w_o,那么n(w, i)表示从根节点到叶节点w路径中的第i个节点,v'(w, i)表示n(w, i)所对应的v'向量。
注意:v'不是针对词语w而言,而是针对节点n,每个节点n都有自己的一个向量v',而不是每个词在每个节点上有一个向量,或者说,这些词在同一个节点上共享向量。
假设h是w_i前面所计算出来的hidden vector,我们在非叶子节点中使用该节点处的v'向量和h点乘,再用sigmoid去判断向左还是向右:(取代softmax)
那么每个叶节点会有一个概率p(wi=wo),最终我们需要极大化从根节点到预测单词w_o这条路径的概率,比如对于目标单词w2,我们需要极大化p(w2=w_o):
在根节点处左右概率之和是1,然后在接下来的每个节点,对应两个子节点的概率值之和等于父节点本身的概率值,那么走到最后,所有叶子节点的概率值之和必定还是等于1:
这也就保证了原始softmax概率和为1的前提,因此可以用层次sigmoid去代替softmax函数。
Loss函数定义为:
极大化目标单词的路径概率。
现在我们重新定义v'为:
那么对于W',经过求导,v'更新公式为:
也就是说,这里只需要更新L(w)-1个v'向量,时间复杂度直接从O(V)降到了O(logV)。
关于空间复杂度,原始方法中每个单词需要一个v'向量,总共需要V个向量,而HS中每个节点也会有一个v'向量,总共需要V-1个向量,这些向量维度是一样的,并不会增加空间复杂度。
二. Negative Sampling
NS仅仅选择一小部分列向量进行更新,和HS相比,显得相对简单一点。
对于每条数据,首先我们将原始的V个词划分成正样本w_o和负样本w_neg,正样本也就是要预测的单词,剩下的就是负样本。负样本非常多,我们需要采样出K个负样本,与正样本一起训练。从前我们需要对所有V个词进行softmax计算,现在对于我们只使用到了正样本和负样本,只针对这几个词进行计算,计算量可以大大减小。
负样本选取方式:
NS是一种概率采样的方式,可以根据词频进行随机抽样,我们倾向于选择词频比较大的负样本,比如“的”,这种词语其实是对我们的目标单词没有很大贡献的。
Word2vec则在词频基础上取了0.75次幂,减小词频之间差异过大所带来的影响,使得词频比较小的负样本也有机会被采到。
Loss函数定义为:
极大化正样本出现的概率,同时极小化负样本出现的概率,以sigmoid来代替softmax,相当于进行二分类,判断这个样本到底是不是正样本。
那么对于W',经过求导,v'更新公式为:
也就是说,这里不需要更新所有v'向量,只需要更新部分v'向量,这里的wj是正样本w_o和负样本w_neg的集合,只更新这些样本所对应的v'向量。
Part IV:衡量指标
词向量的衡量指标通常有以下几种:
1)词汇相似度任务,比如wordsim353,但是这种方式比较依赖于数据集。
2)类比任务,比如男人-女人=国王-王后
3)应用于实际任务上的效果,比如文本分类,情感分析,句法分析,序列标注,阅读理解等等。这种方法我觉得是比较靠谱的,因为我们训练词向量是希望得到一个好的词向量,然后能在别的任务上work。