超有趣的二进制—高效位运算秒懂
附Java/C/C++/机器学习/算法与数据结构/前端/安卓/Python/程序员必读书籍书单大全:
书单导航页(点击右侧 极客侠栈 即可打开个人博客):极客侠栈
①【Java】学习之路吐血整理技术书从入门到进阶最全50+本(珍藏版)
②【算法数据结构+acm】从入门到进阶吐血整理书单50+本(珍藏版)
③【数据库】从入门到进阶必读18本技术书籍网盘吐血整理网盘(珍藏版)
④【Web前端】从HTML到JS到AJAX到HTTP从框架到全栈帮你走更少弯路(珍藏版)
⑤【python】书最全已整理好(从入门到进阶)(珍藏版)
⑥【机器学习】+python整理技术书(从入门到进阶已经整理好)(珍藏版)
⑦【C语言】推荐书籍从入门到进阶带你走上大牛之路(珍藏版)
⑧【安卓】入门到进阶推荐书籍整理pdf书单整理(珍藏版)
⑨【架构师】之路史诗级必读书单吐血整理四个维度系列80+本书(珍藏版)
⑩【C++】吐血整理推荐书单从入门到进阶成神之路100+本(珍藏)
⑪【ios】IOS书单从入门到进阶吐血整理(珍藏版)
-------------------------------------------------------------------------------------------------------------------------------------------
我们来看上一篇的一个Varint算法,这个算法的目的是为了令一个整型占用更少的字节,比如小于127的数字,只需占用一个字节即可,小于16384的数字,采用2个字节即可。算法如下:
while (true) {
if ((value & ~0x7F) == 0) {
buffer[position++] = (byte) value;
return;
} else {
buffer[position++] = (byte) ((value & 0x7F) | 0x80);
value >>>= 7;
}
}我们来看看具体图例:
我们看到在小于2097153期间,占用空间会小于4个字节,这个优势还比较明显,不过也有弊端,比如超过268435456之后会有占用5个字节,考虑到大多数情况下,并不会应用到这么大的数字,优化空间方面还是不错的。
通过上述算法实现,我发现优秀的应用算法都会大量用到了位运算,而位运算在工作中却很少用到。位运算速度要快于整数运算的,特别是整数乘法,需要10个或者更多个时钟,若果采用移位操作一个或者2个时钟就够了,不过由于我们常采用十进制来进行算术运算,对二进制的位运算不够熟悉,阅读起来会比较耗费精力,所以借助上述算法实现,我们分析一下位运算的优势以及应用,从而更好的理解二进制。上述代码中,有运用到移位操作,位运算,字节序等相关知识点,我们一一分析。
进位制
我们知道,计算机的存储和处理的信息都是以二进制的,虽然在编写程序的期间数运算还是采用10进制表示,但到机器执行的时候,还会以2进制来进行处理。对于有10个指头的人来说,熟知10进制是很自然的事情,你看教小孩子数学的时候,都是先从数指头开始的,那么若是我们只有2个指头,是不是我们现在会更好理解二进制了?
其他进制转换10进制
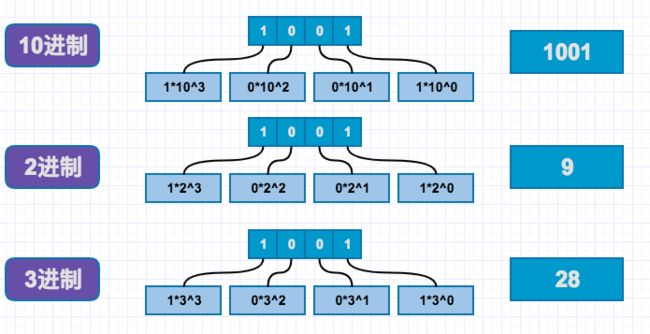
大多数教材会教大家二进制和十进制如何互换,但多数说都是死记硬背式的,并没有去讲解真正含义,换一个进制之后,依然不会,我们回到最根本的一些计数方法上,从10进制来推算。比如我们看一个数字1001,采用十进制表示是:1x10^3+0*10^2+0*10^1+1*10^0。首先从右往左,我们可以看成是从低位到高位,每高一位,指数+1,其次10进制是以10为底数,其三这个公式是采用10进制算术进行计算的(用什么进制算出答案就相当于把当前进制转换为了什么进制了)。这个方式适合所有的进制转换,理解了这个,后续的进制转换都会很容易理解。
2进制的比较简单,我们直接忽略,我们来看下应用到3进制,同样是1001,转换10进制公式:1x3^3+0*3^2+0*3^1+1*3^0=28,我们发现只是底数改变,因为是3进制,所以以3为底数,另外计算方式还是采用10进制算式计算,这表明用10进制算出的答案,就相当于3进制转换为10进制,1001转换为10进制就是28。
那为何不采用其他进制来计算?采用其他进制计算,那么其他进制的乘法口诀你的熟练一遍了,比如10进制的99乘法口诀,你用其他进制的乘法口诀得自己来演绎一遍了,如此这个和我们的常用习惯有些相驳,换算起来会比较慢,所以一般采用十进制与其它进制互转或者作为中间步骤来处理。
10进制转换为其他进制
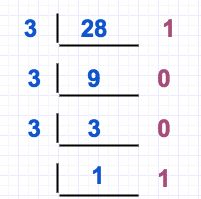
采用上述方法后,我们已经可以做到所有进制转换,包括10进制转3进制,比如十进制28转换为3进制28=2*3+22,这个采用3进制(3的三进制表示10)来进行计算,但是会很麻烦。所以10进制转换其他进制,我们常采用短除法,如下:
当前数不断除以3并把余数作为新的最高位,28除以3余1,1为“个位”,9除以3余0,0为“十位”,3除以3余0,0为“百位”,最终的1是“千位”。如果我们有注意到前面的3进制转10进制算法,我们可以发现短除法其实是3进制转10进制的逆操作,比如3进制转换为十进制时候是:1*3^3+0*3^2+0*3^1+1*3^0 ,我们转换一下是((1*3+0)*3+0)*3+1,如此和10进制转换3进制的时候逆向操作。
小数
如果前面的理解了,小数就可以很容易理解了,我们还是先从10进制来看。比如十进制12.34,我们看小数后面十分位部分.3,表示把1分为10份只取3份,.04百分位部分是把1分为100份,取4份。那么我们换成公式:
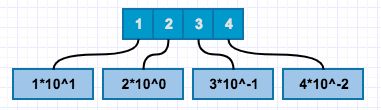
12.34=1*10^1+2+3*(1/10)+4*(1/100)
=1*10^1+2+3*10^-1+4*10^-2我们看到小数部分还是以进制为底数,不过指数部分采用了负数,点的左边的位的指数是位的正幂,点数的右边是位的指数负幂。理解了这个,其他进制的小数部分也就了解, 它们是相同的,比如二进制1001.101:
有了这个理解,我们后续的浮点数就比较好理解了,IEEE浮点表示浮点数,也是基于这种方式,只是定义了些规范,后续我们会详细了解。
移位操作
常见的移位操作有三种:左移,逻辑右移,算术右移。
移动操作
| 操作 | 值 |
| 参数x | [01100011] [10010101] |
| x<<4 | [00110000] [01010000] |
| x>>4(逻辑右移) | [00000110] [00001001] |
| x>>4(算术右移) | [00000110] [11111001] |
左移
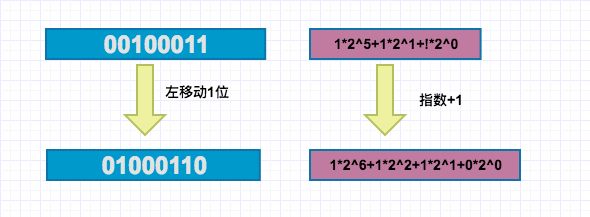
x向左移动k位,会丢弃最高的k位,并在右端补k个0,也就是常说的当前值乘以2的k次方。为何是乘以2的k次方?我们看10进制的时候,某数乘以10,就是在末尾增加1个0 ,由此我们可以联想到,二进制左移一位(末尾加一个0)相当于乘以2,这个结论普遍存在于所有进位制中:k进制数的末尾加个0,相当于该数乘以k。
我们从图中可以看到,左移动一位,就相当于进位制展开式的每个指数都加1,如此移动一位,就相当于当前数(1*2^5+1*2^1+!*2^0)*2^1=1*2^6+1*2^2+1*2^1
右移
理解了左移的原理,右移动的原理也是相同的,右移k位=进位制展开式的每个指数都减k,也就是当前数除以进制的k次方。唯一不同的是分为逻辑右移和算术右移。
逻辑右移就是无符号移位,右移几位,就在左端补几个0,比如上边 Varint中每次右移7位,相应的当前数高位就会补充7个0。
算术右移动是有符号移位,和逻辑右移不同的是,算术右移是在左端补k个最高有效位的值,如此看着有些奇特,但对有符号整数数据的运算非常有用。我们知道有符号的数,首位字节,是用来表示数字的正负。负数采用补码形式来存储,比如[11100110],10进制是-26,算术右移1位之后[11110011],10进制是-13,如若不是补最高有效位的值1而是补做事0的话,右移之后就变成正数了。
字节序
单个字节并没有字节序的问题,当一个数据需要多个字节存储的时候,就会牵扯到这样的问题,这个数据的地址是什么,存储器中如何排列这些字节,是高位地址存最高有效位,还是低位地址存最高有效位。
比如一个int类型的变量,它的地址是使用字节中最小的地址,比如在存储器上的位置是0x101、0x102、0x103,它的地址是0x101,若是这个数据是一个w位的整数,位表示为[x(w-1),x(w-2)....,x1,x0],那么其中x(w-1)是最高有效位,x0是最低有效位,w若是8的倍数,位被分组成字节,那么最高有效字节是[x(w-1)...x(w-8)],最低有效字节是[x7,x6...x0]。这个也可以成为物理顺序,和我们普通人理解的存储顺序预期相符合,比如十进制也是高位(百位,10位)在地位(个位)前面。
小端法(little endian)
如果字节的逻辑顺序与物理顺序相反,也就是w的最低有效字节在前面[x7,x6....x0],最高有效字节[x(w-1)...x(w-8)]在后面,此时成为小端法(little endian)。多数intel兼容机都采用这种规则。
大端法(big endian)
如果字节的逻辑顺序与物理顺序相同,也就是w的最低有效字节[x(w-1)...x(w-8)]在前面,最高有效字节[x7,x6....x0]在后面,称为大端法(big endian),大多数IBM和SunMicrosystems的机器都是采用这种规则。
比如一个十六进制数:0x01234567,我们用大端小端法看他们在存储器上的位置。
我们可以看到大端法是比较符合我们习惯的,高位在前地位在后。
上述Varint的算法,是采用小端法来存储字节顺序的。
buffer[position++] = (byte) ((value & 0x7F) | 0x80);每次都是获取当前数据的后7个字节存储到数据流buffer里面,也就是低位字节放在buffer字节数组的前面。
数独
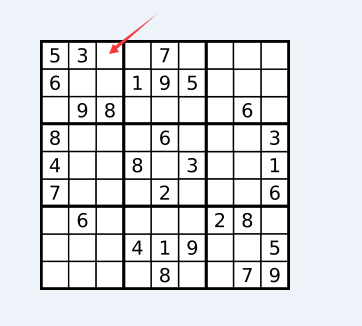
数独是介绍位运算的好例子,运用位运算和不运用效率差别还是挺大的。我们先看数独需求:
1、当前数字所在行数字均含1-9,不重复
2、当前数字所在列数字均含1-9,不重复
3、当前数字所在宫(即3x3的大格)数字均含1-9,不重复(宫,如下图每个粗线内是一个宫)
常规算法
若是我们采用常规方式的,每填写一个数字,需要检查当前行、列,宫中其他位置是否有重复数字,极端情况下需要循环27(3*9)次来进行检查,我们看下常规算法下check
int check(int sp) {
// 檢查同行、列、九宮格有沒有相同的數字,若有傳回 1
int fg= 0 ;
if(!fg) fg= check1(sp, startH[sp], addH) ; // 檢查同列有沒有相同的數字
if(!fg) fg= check1(sp, startV[sp], addV) ; // 檢查同行有沒有相同的數字
if(!fg) fg= check1(sp, startB[sp], addB) ; // 檢查同九宮格有沒有相同的數字
return(fg) ;
}
int check1(int sp, int start, int *addnum) {
// 檢查指定的行、列、九宮格有沒有相同的數字,若有傳回 1
int fg= 0, i, sp1 ;
//万恶的for循环
for(i=0; i<9; i++) {
sp1= start+ addnum[i] ;
if(sp!=sp1 && sudoku[sp]==sudoku[sp1]) fg++ ;
}
return(fg) ;
}这个效率是否很吓人,每次填写一个就需要check27次,有木有check一次的算法?当然有了,采用位运算,一次搞定。来我们看下位运算的思路:
位运算
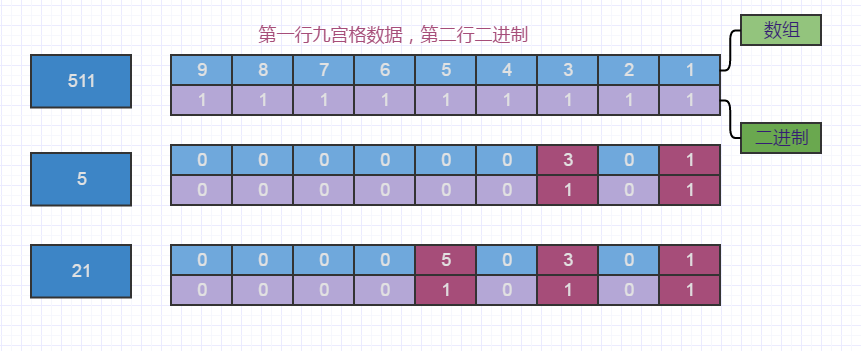
我们看上图所示,单个行(或者列、宫)数据,都是有1-9共9个数字,我们统称为九宫数字。若是我们采用二进制,以九宫数字充当二进制数据的位坐标,采用9位的二进制就可以与之一一对应,位上有数据,标识为1,无数据标识为0,如此一个正数就能解决一行九宫数据状态,无需需存一个数组。
比如 看图中深红色部分,当前九宫数据中已经有1和3,那么二进制右起第一位和第三位标识为1,一个数字5就可以存下当前行(或者列、宫)数组状态了,如若数字为511表明,所有的九宫数字都用完了,如图第一行。
check一个数字是否已经被占用了,可以采取位运算来获取二进制的右数第k位来查看是否是1,若是1,表明指定数字已经被占用了。我们看下具体check算法:
// sp 是当前位置索引,indexV 行索引,indexH 列索引,indexB九宫格索引
int check(int sp,int indexV,int indexH,int indexB) {
// 检查同行、列、九宮格沒有用到的数字,若已经用过返回 1
int status = statusV[indexV]|statusH[indexH]|statusB[indexB];
//9个数字都被用了
if (status>=STATUS_MAX_VALUE)
{
return 1;
}
int number=sudoku[sp];
//取右数第k位,若是1表明这个值已经存在了
return status>>(number-1)&1;
}
// 行、列、宫二进制数据指定位置标记为1
int markStatus(int indexV,int indexH,int indexB,int number){
if (number<1)
{
return 0;
}
//把右数第k(从1计数)位变成1
statusV[indexV]|=(1<<(number-1));
statusH[indexH]|=(1<<(number-1));
statusB[indexB]|=(1<<(number-1));
}我们以以下图例位置举例,如何获得当前位置可以填取的数字
可以看到2个位运算就解决了检查可用数字的操作了,而之前常规算法,需要用27次查找才可以获取到。当然了这个算法还可以优化,比如采用启发式DFS,搜索可用数字,速度更快,感兴趣可点击这里。
常规算法和位运算算法C语言代码,我已经上传码云了,想了解的点击下面链接,自行去查看去。(常规算法google的)
地址: 常规算法数独,位运算版本数独
基础
位操作符
| 符号 | 含义 | 规则 |
|---|---|---|
| & | 与 | 两个位都为1时,结果为1 |
| | | 或 | 有一个位为1时,结果为1 |
| ^ | 异或 | 0和1异或0都不变,异或1则取反 |
| ~ | 取反 | 0和1全部取反 |
| << | 左移 | 位全部左移若干位,高位丢弃,低位补0 |
| >> | 算术右移 | 位全部右移若干位,,高位补k个最高有效位的值 |
| >> | 逻辑右移 | 位全部右移若干位,高位补0 |
注意:
1、位运算只可运用于整数,对于float和double不行。
2、另外逻辑右移符号各种语言不太同,比如java是>>>。
3、位操作符的运算优先级比较低,尽量使用括号来确保运算顺序。比如1&i+1,会先执行i+1再执行&。
应用实例
很棒的应用实例,你可以mark一下,方便以后对照使用。
1、混合体
位运算实例
| 位运算 | 功能 | 示例 |
|---|---|---|
| x >> 1 | 去掉最后一位 | 101101->10110 |
| x << 1 | 在最后加一个0 | 101101->1011010 |
| x << 1 | 1 | 在最后加一个1 | 101101->1011011 |
| x | 1 | 把最后一位变成1 | 101100->101101 |
| x & -2 | 把最后一位变成0 | 101101->101100 |
| x ^ 1 | 最后一位取反 | 101101->101100 |
| x | (1 << (k-1)) | 把右数第k位变成1 | 101001->101101,k=3 |
| x & ~ (1 << (k-1)) | 把右数第k位变成0 | 101101->101001,k=3 |
| x ^(1 <<(k-1)) | 右数第k位取反 | 101001->101101,k=3 |
| x & 7 | 取末三位 | 1101101->101 |
| x & (1 << k-1) | 取末k位 | 1101101->1101,k=5 |
| x >> (k-1) & 1 | 取右数第k位 | 1101101->1,k=4 |
| x | ((1 << k)-1) | 把末k位变成1 | 101001->101111,k=4 |
| x ^ (1 << k-1) | 末k位取反 | 101001->100110,k=4 |
| x & (x+1) | 把右边连续的1变成0 | 100101111->100100000 |
| x | (x+1) | 把右起第一个0变成1 | 100101111->100111111 |
| x | (x-1) | 把右边连续的0变成1 | 11011000->11011111 |
| (x ^ (x+1)) >> 1 | 取右边连续的1 | 100101111->1111 |
| x & -x | 去掉右起第一个1的左边 | 100101000->1000 |
| x&0x7F | 取末7位 | 100101000->101000 |
| x& ~0x7F | 是否小于127 | 001111111 & ~0x7F->0 |
| x & 1 | 判断奇偶 | 00000111&1->1 |
2、交换两数
int swap(int a, int b)
{
if (a != b)
{
a ^= b;
b ^= a;
a ^= b;
}
}
3、求绝对值
int abs(int a)
{
int i = a >> 31;
return ((a ^ i) - i);
}
4、二分查找32位整数前导0个数
int nlz(unsigned x)
{
int n;
if (x == 0) return(32);
n = 1;
if ((x >> 16) == 0) {n = n +16; x = x <<16;}
if ((x >> 24) == 0) {n = n + 8; x = x << 8;}
if ((x >> 28) == 0) {n = n + 4; x = x << 4;}
if ((x >> 30) == 0) {n = n + 2; x = x << 2;}
n = n - (x >> 31);
return n;
}5、二进制逆序
int reverse_order(int n){
n = ((n & 0xAAAAAAAA) >> 1) | ((n & 0x55555555) << 1);
n = ((n & 0xCCCCCCCC) >> 2) | ((n & 0x33333333) << 2);
n = ((n & 0xF0F0F0F0) >> 4) | ((n & 0x0F0F0F0F) << 4);
n = ((n & 0xFF00FF00) >> 8) | ((n & 0x00FF00FF) << 8);
n = ((n & 0xFFFF0000) >> 16) | ((n & 0x0000FFFF) << 16);
return n;
}6、 二进制中1的个数
unsigned int BitCount_e(unsigned int value) {
unsigned int count = 0;
// 解释下下面这句话代码,这句话求得两两相加的结果,例如 11 01 00 10
// 11 01 00 10 = 01 01 00 00 + 10 00 00 10,即由奇数位和偶数位相加而成
// 记 value = 11 01 00 10,high_v = 01 01 00 00, low_v = 10 00 00 10
// 则 value = high_v + low_v,high_v 右移一位得 high_v_1,
// 即 high_v_1 = high_v >> 1 = high_v / 2
// 此时 value 可以表示为 value = high_v_1 + high_v_1 + low_v,
// 可见 我们需要 high_v + low_v 的和即等于 value - high_v_1
// 写简单点就是 value = value & 0x55555555 + (value >> 1) & 0x55555555;
value = value - ((value >> 1) & 0x55555555);
// 之后的就好理解了
value = (value & 0x33333333) + ((value >> 2) & 0x33333333);
value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f);
value = (value & 0x00ff00ff) + ((value >> 4) & 0x00ff00ff);
value = (value & 0x0000ffff) + ((value >> 8) & 0x0000ffff);
return value;
// 另一种写法,原理一样,原因在最后一种解法中有提到
//value = (value & 0x55555555) + (value >> 1) & 0x55555555;
//value = (value & 0x33333333) + ((value >> 2) & 0x33333333);
//value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f);
//value = value + (value >> 8);
//value = value + (value >> 16);
//return (value & 0x0000003f);
}