FBGEMM 开源,用于最先进的服务器端推理
以下内容翻译自:Open-sourcing FBGEMM for state-of-the-art server-side inference
- Facebook 正在开源 FBGEMM,这是一个针对服务器端推理进行了优化的高性能内核库。
- 深度学习模型加速会使用低精度计算,与其他常用库不同,FBGEMM 优化了 CPU 上的低精度计算性能。
- 该库已在 Facebook 部署,它的性能与目前的生产基准相比提升超过2倍。
- FBGEMM 在原生张量格式上提供了高性能(与许多其他需要重新打包张量以获得最佳性能的库不同)。
- 它通过在运行时生成高性能的特定于形状和大小的内核,提供了大量即插即用功能和性能。
为了使大规模生产服务器能够有效地运行最新、最强大的深度学习模型,我们创建了 FBGEMM,一种低精度、高性能的矩阵乘法和卷积库。FBGEMM 针对服务器端推理进行了优化,与之前提供的替代方案不同,它在使用现代深度学习框架执行量化推理时准确性和效率兼备。通过该库,我们在当前一代 CPU 上实现了相比生产基线2倍以上的性能提升。
我们现在开源用于执行高效的低精度推理的 FBGEMM,所有基本构建模块均打包在单一库中,因而对其他工程师而言十分方便。您现在可以使用 Caffe2 前端部署它,它很快就可以通过 PyTorch 1.0 Python 前端直接调用。
与我们上周开源的移动设备新库 QNNPACK 一起,工程师现在可以获得全面的量化推理支持,而该功能是 PyTorch 1.0 平台的一部分。
FBGEMM 提供以下几个主要功能:
- 与科学计算中使用的传统线性代数库(使用 FP32或 FP64精度)不同,它专门针对低精度数据进行了优化。
- 它为小批量提供有效的低精度通用矩阵—矩阵乘法(GEMM),并支持精确度损失最小化技术,如行间量化和异常值感知量化。
- 它还利用 GEMM 操作前后的融合机会,以克服在带宽限制下低精度矩阵乘法的独特挑战。
FBGEMM 已经在 Facebook 大规模部署,在那里端到端地使许多人工智能服务受益,包括将英语到西班牙语的翻译速度提高1.3倍,令信息流中推荐系统的 DRAM 带宽使用率减少了40%,使 Rosetta 中的字符检测速度获得2.4倍加速。Rosetta 是我们用于理解图像和视频中的文本的机器学习系统。Rosetta 对于 Facebook 和 Instagram 上的许多团队而言有多种多样的用途,包括自动识别违反我们政策的内容,更准确地对照片进行分类,以及为使用我们产品的人呈现更加个性化的内容。
为什么 GEMM 效率很重要
全连接(FC)算子在 Facebook 数据中心部署的深度学习模型中消耗了最多的浮点运算(FLOP)。我们在 Facebook 的生产代表模型中对 FLOP 使用情况进行了数据中心范围的分析。下面的饼图显示了在24小时内测量的数据中心深度学习推理 FLOP 的分布情况。
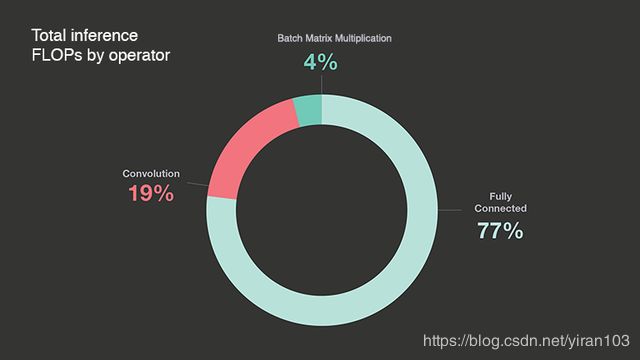
FC 算子只是简单的 GEMM,因此整体效率直接取决于 GEMM 效率。许多深度学习框架将卷积实现为 im2col,然后 GEMM,因为高性能计算(HPC)领域中的线性代数库中可以使用高性能 GEMM 实现。但是直接 im2col 增加了输入数据重叠复制的开销,因此一些深度学习库也实现了直接(无 im2col)卷积以提高效率。如下面更详细的解释,我们提供了一种融合 im2col 与主 GEMM 内核的方法,以最大限度地减少 im2col 开销。高性能 GEMM 内核是一个关键部分,但它并不是唯一的一个。通常,HPC 库提供的内容与深度学习推理的要求之间并不匹配。HPC 库通常不支持高效的量化 GEMM 相关操作。它们没有针对深度学习推理中常见的矩阵形状和大小进行优化。并且他们没有利用权重矩阵恒定的性质。
深度学习模型通常使用 FP32数据类型来表示激活和权重,但具有混合精度数据类型(8位或16位整数,FP16等)的计算通常更高效。最近行业和研究方面的工作表明,使用混合精度的推理不会对准确性产生不利影响。FBGEMM 使用这种替代策略,并通过量化模型提高推理性能。此外,新一代 GPU、CPU 和专用张量处理器本身支持低精度计算基元,例如 Nvidia 张量核心中的 FP16/INT8或谷歌处理器中的 INT8。因此,深度学习社区正在向低精度模型发展。该动向表明量化推断是向正确方向迈出的一步,FBGEMM 提供了一种对当前和下一代 CPU 执行有效量化推理的方法。
理解低精度推理
实现高准确率、低精度推理对于优化深度学习模型至关重要。在开发 FBGEMM 时,我们使用了类似于谷歌论文中详细描述的量化策略。借助于仿射方式的比例因子和零点来量化矩阵中的每个值,因此量化域中的计算直接映射到实域中的计算。这些比例和零点值在矩阵中的多个条目之间共享(例如,所有行可以具有相同的比例和零点)。在下面的等式中, A A A 是实值矩阵, A q A_q Aq 是量化矩阵; a s c a l e a_{\mathrm{scale}} ascale 是实值常量, a z e r o _ p o i n t a_{\mathrm{zero\_point}} azero_point 是量化域中的常量。
A [ i ] = a s c a l e ( A q [ i ] − a z e r o _ p o i n t ) A[i] = a_{\mathrm{scale}}(A_q[i]-a_{\mathrm{zero\_point}}) A[i]=ascale(Aq[i]−azero_point)
利用这种量化框架,我们可以在量化域中表示矩阵-矩阵乘法,如下所示:
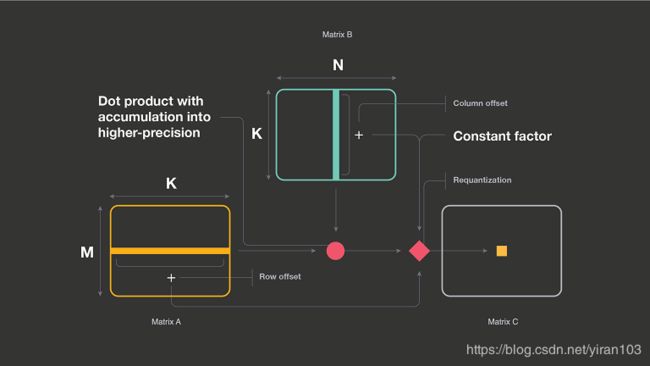
重要的是要注意几个细节:
- C C C 矩阵中的每个输出值 ( i , j ) (i, j) (i,j) 需要 A A A 矩阵的第 i i i 行(行偏移), B B B 矩阵的第 j j j 列(列偏移)以及加到点乘积的常数因子。
- 如果其中一个矩阵是常数,则常数因子计算可以与该矩阵的行(或列)偏移计算相结合。这些偏移稍后在二次量化步骤期间使用。
- 点乘结果累积到更高的精度,然后缩小到下一层的精度。我们将此过程称为二次量化。
这些背景细节强调,当我们执行低精度 GEMM 时,围绕它的其他操作对整体效率同样重要。如果没有和低精度 GEMM 一样仔细地执行这些额外的操作(例如行偏移计算或累加后量化),它们可能抵消低精度运算的收益。
深入研究 FBGEMM 的主要功能
FBGEMM 在若干方面与其他库不同:
- 它将小型计算与带宽限制操作相结合。
- 它通过将 GEMM 后操作与宏内核融合来利用缓存局部性,并支持降低精确度损失的操作。
- 它提供模块化构建块,根据需要构建整个 GEMM 管道,从而在不同的前端和后端组件中即插即用。
FBGEMM 的一个关键组成部分是高性能的低精度 GEMM,我们使用的方法类似于其他研究工作(Goto等人和 BLIS 框架)针对 FP32和 FP64数据类型而非低精度的方法。以下示例代码显示了在现代 CPU 架构上实现高性能 GEMM 的典型方法。这里 M、N 和 K 是标准矩阵维度:A是 MxK 矩阵,B 是 KxN 矩阵,C 是 MxN 矩阵。MCB、NCB、KCB、MR 和 NR 是特定于目标的常量,它们的值取决于给定 CPU 上的可用高速缓存和寄存器(CB表示高速缓存块,R表示寄存器。)。将简单的三循环矩阵-矩阵乘法转换成以下围绕微内核的五个循环,从而适用于具有多级高速缓存和向量寄存器的 CPU 存储器层次结构。
Loop1 for ic = 0 to M-1 in steps of MCB
Loop2 for kc = 0 to K-1 in steps of KCB
//Pack MCBxKCB block of A
Loop3 for jc = 0 to N-1 in steps of NCB
//Pack KCBxNCB block of B
//--------------------Macro Kernel------------
Loop4 for ir = 0 to MCB-1 in steps of MR
Loop5 for jr = 0 to NCB-1 in steps of NR
//--------------------Micro Kernel------------
Loop6 for k = 0 to KCB-1 in steps of 1
//update MRxNR block of C matrix
如该示例所示,高性能 GEMM 实现通过将当前使用的A和B矩阵块打包成在最内层微内核中顺序访问的较小块来工作。这里的“打包”是指将矩阵数据重组为另一个阵列,使得优化实现的内核中的访问模式是顺序的。内核中数据的顺序访问对于在现代硬件架构上实现高效带宽非常重要。打包是带宽限制操作,因为它只读取和写入数据。因此,如果我们可以将小型计算操作与带宽限制打包操作相结合,则计算成本会重叠,并且总体打包时间保持不变。
我们利用打包例程的带宽限制特性,并将简单的计算操作与打包相结合。下图显示了我们迄今为止实施的各种包装程序。例如,PackingWithRowOffset执行行偏移计算,同时以内层内核所需格式重新组织数据。仅针对当前正被打包的块(即,MCBxKCB 块)计算行偏移。这些行偏移稍后在 GEMM 后二次量化流水线中使用。在打包时计算行偏移的优点是我们不需要对A矩阵数据进行两次传递,从而避免多次将数据移动到CPU并避免缓存污染。在重用其余流程时还可以添加较新的打包例程。
值得注意的是,推理所用 GEMM 中的矩阵之一是权重矩阵,并且在推理期间是恒定的。因此,我们可以预先包装一次并将其多次用于不同的激活,从而避免了重新打包的成本(在上面的代码中显示在 Loop3 中)。如果激活矩阵很小,则打包权重矩阵的相对成本可能很大。 但是通用 GEMM 实现必须支付这个成本,这些实现并未专门针对其中一个矩阵是不变的情况而设计。
FBGEMM 从头开始设计,同时牢记这些要求。它允许我们使用预先打包的矩阵,这避免了大量的内部存储器分配,并允许融合 GEMM 后操作,如非线性、偏置加法和二次量化。FBGEMM 库将量化目标定为8位整数,因为我们的目标硬件有效地支持8位整数运算。
上图显示了我们保持核心计算不变的同时,组合A和B矩阵的不同打包方法,然后构建输出操作的管道。FBGEMM 实现允许您通过选择A的任意打包例程,B的任意打包例程,任意核心内核(累积到 INT16、INT32或 FP32)以及 GEMM 后操作的任意组合来构建管道。设计是可扩展的,并且可以根据需要将新的打包或后期操作添加到 FBGEMM 库中。gemmlowp 库还允许使用称为输出管道的 GEMM 后操作组成核心内核,但 FBGEMM 将其扩展为输入打包。
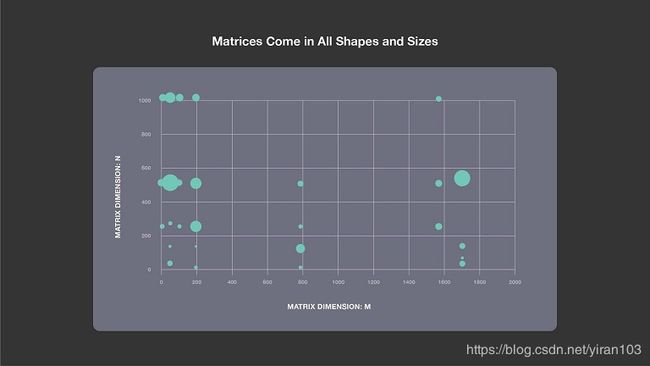
通常,来自 HPC 领域的 GEMM 库针对方形或近似正方形的大矩阵进行了优化。对于网络中的矩阵乘法,以用于 Rosetta、Resnet50、Speech 和 NMT 的 Faster-RCNN 为例,其中最常出现的形状如下图所示。
每个气泡代表矩阵-矩阵乘法的典型 M、N 和 K 维度。气泡的大小与 K 值成正比。从图中可以清楚地看出,矩阵有各种形状和大小。 M 有时非常小,而在其他时候 N 非常小。我们需要针对以上所有情况的高效实现。
对于内核,FBGEMM 秉承的思想是“一种尺寸不适合所有”,因此根据矩阵形状动态生成高效的矢量化代码。例如,如果我们在运行时看到 M 是1,我们查询 M = 1 是否存在有效内核,如果有,则使用它。如果没有,我们生成该内核,将其存储在内核缓存中,并使用它。我们仅需仔细制作几个内核,然后将其他矩阵维度映射到它们。
总的来说,我们实现的优化循环结构如下所示:
Loop1 for ic = 0 to M-1 in steps of MCB
Loop2 for kc = 0 to K-1 in steps of KCB
//Pack MCBxKCB block of A
Loop3 for jc = 0 to N-1 in steps of NCB
//--------------------Inner Kernel------------
//Dynamically generated inner kernel
//Loop4 and Loop5 are in assembly
FBGEMM 是一个 C++库,下面的代码清单显示了它公开的 GEMM 接口。灵活的接口是基于 C++模板实现的。
template<
typename packingAMatrix,
typename packingBMatrix,
typename cT,
typename processOutputType>
void fbgemmPacked(
PackMatrix<packingAMatrix,
typename packingAMatrix::inpType,
typename packingAMatrix::accType>& packA,
PackMatrix<packingBMatrix,
typename packingBMatrix::inpType,
typename packingBMatrix::accType>& packB,
cT* C,
void* C_buffer,
std::int32_t ldc,
const processOutputType& outProcess,
int thread_id,
int num_threads);
该接口专门设计用于支持优化的量化推理和 GEMM 后操作的融合。模板参数 packA 和 packB 为当前块提供打包例程。因为 FBGEMM 是针对推理的,所以我们假设已打包好 B 矩阵(即从不调用 packB.pack 函数)。接下来的三个参数与 C 矩阵有关。 C 是指向 C 矩阵本身的指针。 C_buffer 是指向预分配缓冲存储器的指针,用于存储中间32位整数或 FP32值。并且 ldc 是 C 矩阵的标准主维。outProcess是一个模板参数,可以是实现处理输出元素管道的 C++函数。在 C 矩阵中计算 C 矩阵块之后调用它以利用缓存局部性。最后两个参数与并行化有关。在内部,FBGEMM 有意设计为不创建任何线程。通常,这样的库旨用作深度学习框架(如 PyTorch 和 Caffe2)的后端,这些框架可以创建和管理自己的线程。总的来说,该接口允许使用不同的打包方法以及在当前计算的输出矩阵块上构建 GEMM 后操作的流水线。
由于深度卷积与 GEMM 有很大不同,所以我们在 FBGEMM 中还包含了一个专门的内核。 我们相信,我们的数据中心(包括卷积)中发现的大多数重要用例都可以使用我们编写各种输入打包和输出处理操作的方法有效地实现。和 QNNPACK 一样,我们的深度卷积内核在通道上进行矢量化。但因为代码大小限制不像移动平台那样严格,我们进行更积极的展开和内联模板特化。与 QNNPACK——需要准备各种二次量化选项,包括目标平台缺乏良好的浮点支持时纯粹使用定点操作相比,FBGEMM 在二次量化期间使用 FP32 操作将 INT32 中间 GEMM 输出定标到 INT8。
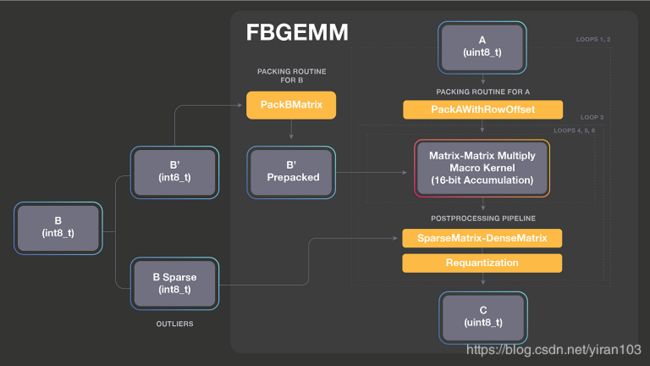
端到端 FBGEMM 管道示例
FBGEMM 接口允许灵活组合各种输出处理方案。下图展示了我们如何执行16位累加。FBGEMM 支持 INT8矩阵乘法和 INT16累加,以在计算限制情形下获得更好的性能。INT8 FMA 累积到 INT16是组合使用vpmaddubsw和vpaddsw向量指令执行的。使用 INT8与 FP32相比,每个向量指令处理的元素多4倍,但我们对每个向量 FMA 使用两个向量指令。因此,累积到16位的理论峰值是 FP32的2倍。然而,INT16累加通常会导致频繁的溢出(饱和),我们通过使用异常值感知量化来避免这种情况。也就是说,我们将矩阵 B 分成 B = B ′ + B s p a r s e B = B'+ B_\mathrm{sparse} B=B′+Bsparse,其中 B’只有小量级的数字,大值被分到 B s p a r s e B_\mathrm{sparse} Bsparse。我们将具有异常数的矩阵表示为 B s p a r s e B_\mathrm{sparse} Bsparse,因为 B 通常只有几个大数,因此 B s p a r s e B_\mathrm{sparse} Bsparse 通常非常稀疏。在切分之后, A × B A \times B A×B 可以通过 A × B ′ + A × B s p a r s e A \times B'+ A \times B_\mathrm{sparse} A×B′+A×Bsparse 计算,其中我们可以安全地使用 INT16累加 A × B ′ A \times B' A×B′,因为 B’仅包含小数字。考虑到 B s p a r s e B_\mathrm{sparse} Bsparse 的稀疏性,大多数计算将在 A × B ′ A \times B' A×B′ 中发生。
因为 B 在推理期间是恒定的,作为预处理步骤,B 的切分、B’的打包以及 B s p a r s e B_\mathrm{sparse} Bsparse 的高效稀疏矩阵格式转换(我们使用压缩的稀疏列)仅需执行一次。FBGEMM 将密集矩阵乘以稀疏矩阵(即 A × B s p a r s e A \times B_\mathrm{sparse} A×Bsparse。注:原文是 A × B ′ A \times B' A×B′ 似乎是笔误。)的乘法计算作为后处理流水线的一部分。稀疏矩阵计算通常是内存带宽限制操作,因此将其与主要计算融合是很重要的。与其分别计算 A × B ′ A \times B' A×B′ 和 A × B s p a r s e A \times B_\mathrm{sparse} A×Bsparse,将二者计算融合在一起,可在打包 A 时计算 A × B s p a r s e A \times B_\mathrm{sparse} A×Bsparse 的一部分,而 C 的部分结果是缓存驻留的。
性能影响和结果
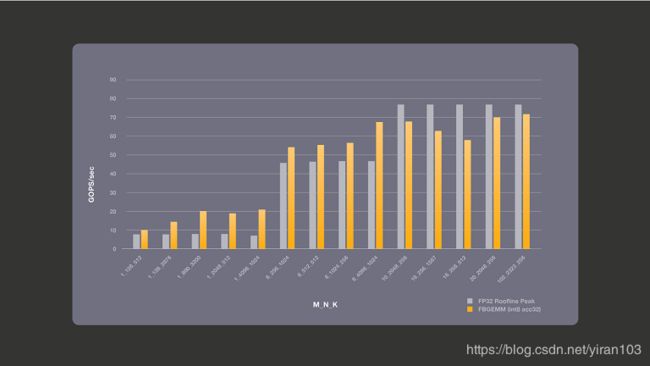
我们在 Intel(R)Xeon(R)CPU E5-2680 v4 上使用单核单个线程运行 FBGEMM 库的性能基准测试。我们使用了基本频率为2.4 GHz 的 Broadwell 机器,禁用了 turbo 模式以获得可靠的批次控制结果。下图显示了 FP32理论峰值数与 INT8 GEMM 累加到16位的实际性能。如前所述,这个 Broadwell 机器累加到16位的理论单核峰值是 FP32峰值的2倍,即每秒153.6千兆操作(GOPS)。对于计算限制的情况,使用累加到16位,从而获得最大性能收益。对于带宽限制情况,累加到16位不会给我们带来更好的性能,但是除非我们使用异常值感知量化,否则累加到16位可能会溢出; 因此,对于带宽限制情况,我们避免使用16位累加。
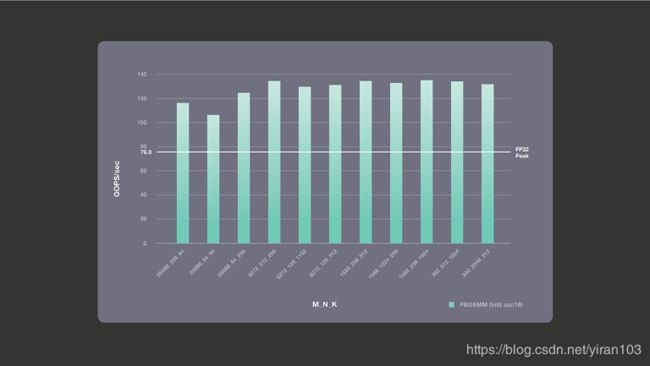
下图显示了带宽限制情况的性能,其中我们执行累积到32位。具有 INT32累积的 INT8 FMA 组合使用vpbroadcastd、vpmaddubsw、vpmaddwd和vpaddd向量指令。由于INT8 FMA 使用了4条指令,因此即使每个元素的尺寸小4倍, INT8的理论计算峰值并不比 FP32好。该图还显示了同一台机器的 roofline 峰值。总体而言,Broadwell 机器的所有核心的理论峰值带宽均为76.8 Gb/s。我们测量了每个核心的流三元组带宽为15.6 GB/s,并使用此数字来计算 roofline 峰值。FP32 roofline 峰值是理论上可能的最高值,在实践中,所获得的性能小于这些 roofline 值。我们将 INT8性能与 FP32的这些理论上最佳数字进行比较。如下图所示,累积到32位对小批量最有利。矩阵维度 M 是批量维。较低精度数据使用更少的带宽,使我们能够实现优于 FP32的理论 roofline 性能。
未来展望
量化推理已经证明对当前一代服务器硬件有用。精心实施的量化已在语言翻译模型、推荐系统以及图像和视频中文本理解模型上产生令人鼓舞的效果。但我们可以借助 FBGEMM 继续推进我们的工作。在 Facebook,很多在用的其他模型尚未实现量化推理,这些场景中深度学习框架相结合 FBGEMM 也有可能提高效率。某些较新的模型,如 ResNeXt-101 和 ResNext3D 更准确,但计算量很大,因此如不提高效率,大规模部署它们会非常耗费资源。我们希望 FBGEMM 能够帮助填补部署所需的效率差距。
随着计算机视觉中的深度学习模型为寻求更高的准确性而变得更宽更深,分组卷积和深度卷积(分组的特殊情况)的使用正在增加。然而,当组的数量很大时,使用 im2col 然后 GEMM 的方法执行分组卷积效率十分低下。我们已经有了深度卷积的专门实现,但我们打算也将直接分组卷积添加到 FBGEMM 中。 最常用的 Caffe2 操作符已经使用 FBGEMM 实现,并且 FBGEMM 直接集成到 PyTorch 也在计划中。我们还计划添加更多功能以进一步提高效率,例如将深度卷积与1×1卷积合并,改进性能调试支持。
我们希望开源 FBGEMM 能够使其他工程师利用这个高性能内核库,我们欢迎来自更广泛社区的贡献和建议。 HPC 社区长期以来为 GEMM 提供了标准接口,并且通过 FBGEMM,我们证明将某些操作与输入和输出打包相结合更有效。我们希望 HPC 社区未来的 GEMM 接口能够从这些想法中获得灵感。
我们要感谢 FBGEMM 团队以及 AI 开发人员平台团队和 AI 系统协同设计团队对该项目的贡献。