动态规划——子序列问题汇总
文章目录
- 1.最大连续子序列和
- 2.最长递增子序列
- 3.最长公共子序列
- 4.最长公共子串
- 5.最小编辑距离
- 后续
1.最大连续子序列和
问题定义

即求一个连续子序列,使的其和最大。例如对于序列{5,-3,4,2}来说,最大子序列为{5,-3,4,2},和为8。对于序列{5,-6,4,2},最大子序列为{4,2},和为6。
因为是求 连续序列,所以我们以 S i S_{i} Si 表示问题状态,代表以 A i A_{i} Ai 结尾的子序列的最大和,则我们有下列动态规划递推:
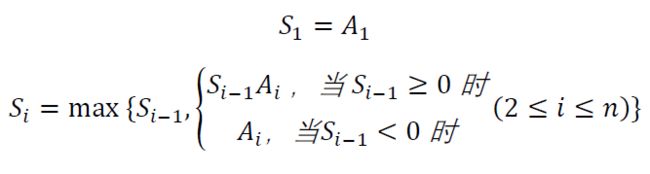
即若前 i i i 项的和不小于0的时候,我们可以接着扩展;否则从第 i i i 项开始另开一个新的子序列。同时,从 S i S_{i} Si 中找最大值。
实现示例
int MSS1(int* num, int len) {
// 每个前缀Ai对应的最大和存储在数组dp[i]中
int* dp = new int[len];
dp[0] = num[0];
for (int i = 1; i < len; i++) {
// 状态转移方程
dp[i] = max(dp[i - 1] + num[i], num[i]);
}
int maxsum = dp[0];
for(int i=1;i<len;i++){
maxsum = maxsum > dp[i] ? maxsum : dp[i];
}
return maxsum;
}
int MSS2(int* num, int len) {
int sum = num[0]; // 这里的sum就代替了dp[i]来求最大值
int maxsum = num[0];
for (int i = 1; i < len; i++) {
if (sum >= 0) sum += num[i];
else sum = num[i];
if (sum > maxsum) maxsum = sum;
}
return maxsum;
}
2.最长递增子序列
问题定义
最长递增子序列(Longest Increasing Subsequence,简写 LIS),给定一个序列 L = { A 1 , A 2 , . . . , A n } L=\{A_{1},A_{2},...,A_{n}\} L={A1,A2,...,An}我们需要找到一个子序列 L i n = { A k 1 A k 2 . . . A k m } L_{in} = \{ A_{k1}A_{k2}...A_{km}\} Lin={Ak1Ak2...Akm},使得 k 1 < k 2 < . . . < k m k_{1} < k_{2} < ...< k_{m} k1<k2<...<km 且 A k 1 < A k 2 < . . . < A k m A_{k1} < A_{k2} < ... < A_{km} Ak1<Ak2<...<Akm,即求解 最长上升子序列。
同样的,我们以 L i L_{i} Li 表示以 A i A_{i} Ai 结尾的子序列的最长长度,则有递推式:
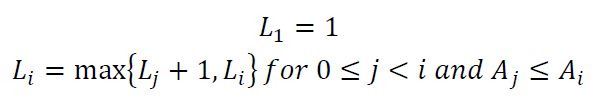
即,对于 A i A_{i} Ai 我们将其尽可能的接到以 A j A_{j} Aj结尾的子序列上,然后求最长长度。注意每个元素在刚开始自成一个上升子序列,即初始化L[i] = 1。
实现示例
int LIS(int* num, int len) {
// 复杂度O(n^2)
int* dp = new int[len];
dp[0] = 1;
for (int i = 1; i < len; i++) {
dp[i] = 1; // 初始化为1
for (int j = 0; j < i; j++) {
if (num[j] < num[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
int maxlen = dp[0];
for (int i = 1; i < len; i++) {
maxlen = maxlen > dp[i] ? maxlen : dp[i];
}
delete[] dp;
return maxlen;
}
3.最长公共子序列
问题定义:
假设有两个序列 A n = { a 0 a 1 a 2 . . . a n − 1 } A_{n} = \{ a_{0}a_{1}a_{2}...a_{n-1}\} An={a0a1a2...an−1} 和 B m = { b 0 b 1 b 2 . . . b m − 1 } B_{m} = \{b_{0}b_{1}b_{2}...b_{m-1}\} Bm={b0b1b2...bm−1}则我们定义一个公共子序列(非连续) Z k = { z 0 z 1 z 2 . . . z k − 1 } Z_{k} = \{z_{0}z_{1}z_{2}...z_{k-1}\} Zk={z0z1z2...zk−1}即存在两组严格递增的的下标(不一定连续) i 0 i 1 . . . i k − 1 i_{0}i_{1}...i_{k-1} i0i1...ik−1和 j 0 j 1 . . . j k − 1 j_{0}j_{1}...j_{k-1} j0j1...jk−1使得 Z k = a i 0 a i 1 . . . a i k − 1 = b j 0 b j 1 b j 2 . . . b j k − 1 Z_{k} = a_{i_{0}}a_{i_{1}}...a_{i_{k-1}} = b_{j_{0}}b_{j_{1}}b_{j_{2}}...b_{j_{k-1}} Zk=ai0ai1...aik−1=bj0bj1bj2...bjk−1则最长公共子序列为 Z k Z_{k} Zk,最长长度为 K K K。
最长公共子序列(Longest Common Subsequence,LCS)的三个特性(从后往前):
- 若 a n − 1 = b m − 1 a_{n-1} = b_{m-1} an−1=bm−1,则 z k − 1 = a n − 1 = = b m − 1 z_{k-1} = a_{n-1} == b_{m-1} zk−1=an−1==bm−1。
因为若找到 a i ( i < n − 1 ) a_{i}(i<n-1) ai(i<n−1) 或 b j ( j < m − 1 ) b_{j}(j<m-1) bj(j<m−1) 满足条件,由于非连续递增下标的特性,还是可以顺延。
此时, z 0 z 1 z 2 . . . z k − 2 z_{0}z_{1}z_{2}...z_{k-2} z0z1z2...zk−2 可递推为 a 0 a 1 a 2 . . . a n − 2 a_{0}a_{1}a_{2}...a_{n-2} a0a1a2...an−2 和 b 0 b 1 b 2 . . . b m − 2 b_{0}b_{1}b_{2}...b_{m-2} b0b1b2...bm−2 的一个公共子序列。 - 若 a n − 1 ≠ b m − 1 a_{n-1} \neq b_{m-1} an−1̸=bm−1,则
- 若 z k − 1 ≠ a n − 1 z_{k-1} \neq a_{n-1} zk−1̸=an−1,则 z 0 z 1 z 2 . . . z k − 1 z_{0}z_{1}z_{2}...z_{k-1} z0z1z2...zk−1 可递推为 a 0 a 1 a 2 . . . a n − 2 a_{0}a_{1}a_{2}...a_{n-2} a0a1a2...an−2 和 b 0 b 1 b 2 . . . b m − 1 b_{0}b_{1}b_{2}...b_{m-1} b0b1b2...bm−1 的一个公共子序列;
- 若 z k − 1 ≠ b m − 1 z_{k-1} \neq b_{m-1} zk−1̸=bm−1,则 z 0 z 1 z 2 . . . z k − 1 z_{0}z_{1}z_{2}...z_{k-1} z0z1z2...zk−1 可递推为 a 0 a 1 a 2 . . . a n − 1 a_{0}a_{1}a_{2}...a_{n-1} a0a1a2...an−1 和 b 0 b 1 b 2 . . . b m − 2 b_{0}b_{1}b_{2}...b_{m-2} b0b1b2...bm−2 的一个公共子序列;
问题表示
因此,假设 C(i,j) 表示以 a i a_{i} ai 和 b j b_{j} bj 结尾的子序列的最长公共子串的长度,数组B(i,j) 元素取自 {0,1,2} 表示问题 C(i,j) 通过哪个子问题求解,即 C(i-1,j-1),C(i-1,j)或C(i,j-1)。
则我们有动态递推公式:
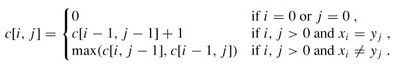
例如两个字符串 X = “ABCBDAB” 和 Y = “BDCABA”,我们有下面求解数组C的过程,先求解第维再递推到高维。
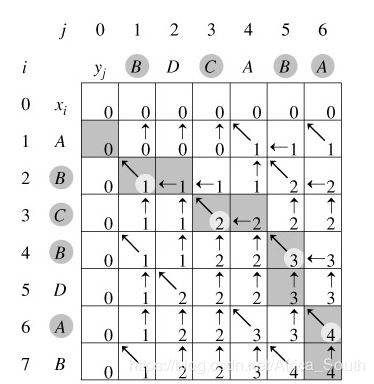
图源来自 yysdsyl的博客
问题求解
/* 最长公共子序列问题 (LCS,非连续)*/
#include例题练习
可参考PAT甲级 1045进行练习,解答示例。
4.最长公共子串
问题描述
最长公共子串(Longest Common Substring) 是最长公共子序列的特殊情况,即
假设有两个字符串序列 A n = { a 0 a 1 a 2 . . . a n − 1 } A_{n} = \{ a_{0}a_{1}a_{2}...a_{n-1}\} An={a0a1a2...an−1} 和 B m = { b 0 b 1 b 2 . . . b m − 1 } B_{m} = \{b_{0}b_{1}b_{2}...b_{m-1}\} Bm={b0b1b2...bm−1}则我们定义一个公共子串(连续) Z k = { z 0 z 1 z 2 . . . z k − 1 } Z_{k} = \{z_{0}z_{1}z_{2}...z_{k-1}\} Zk={z0z1z2...zk−1}即存在两组连续递增的的下标 i 0 i 1 . . . i k − 1 i_{0}i_{1}...i_{k-1} i0i1...ik−1和 j 0 j 1 . . . j k − 1 j_{0}j_{1}...j_{k-1} j0j1...jk−1使得 Z k = a i 0 a i 1 . . . a i k − 1 = b j 0 b j 1 b j 2 . . . b j k − 1 Z_{k} = a_{i_{0}}a_{i_{1}}...a_{i_{k-1}} = b_{j_{0}}b_{j_{1}}b_{j_{2}}...b_{j_{k-1}} Zk=ai0ai1...aik−1=bj0bj1bj2...bjk−1则最长公共子序列为 Z k Z_{k} Zk,最长长度为 K K K。即下标的增长值必须为1。
例如有两个字符序列:
X =
Y =
X和Y的 Longest Common Sequence为
X和Y的 Longest Common Substring为
问题表示
类似于问题3,假设 C(i,j) 表示以 a i a_{i} ai 和 b j b_{j} bj 结尾的子序列的最长公共子串的长度,数组B(i,j) 元素取自 {0,1,2} 表示问题 C(i,j) 通过哪个子问题求解,即 C(i-1,j-1),C(i-1,j)或C(i,j-1)。
则我们有动态递推公式(注意这里下标从1开始):
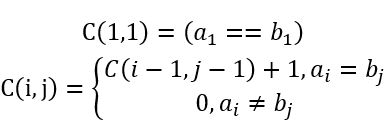
实现示例
/* 最长公共子串 */
#include方法2
也有稍微暴力一点的算法,复杂度都是 O ( m ∗ n ) O(m*n) O(m∗n)。
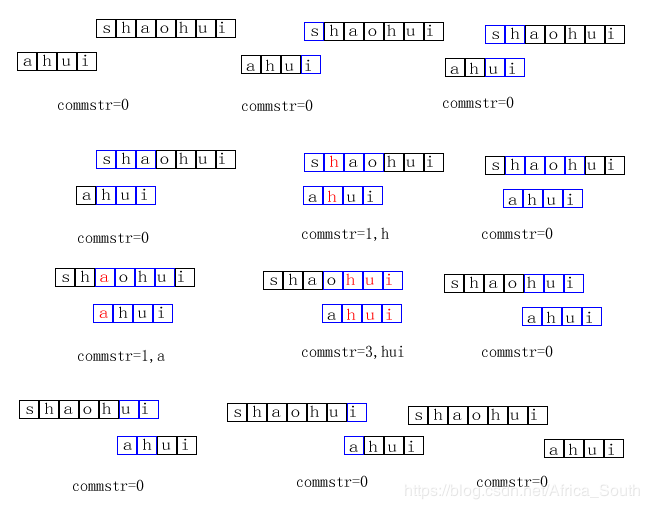
如上图,对于字符串 A=“shaohui” 和字符串 B=“ahui” ,固定字符串A,然后先将字符串B的头部和字符串A的尾巴对齐,然后开始向右移动字符串B,每个求出它们交集的最长公共子串的长度。
(注意,上叙述的头部指的是字符串最右面的位置,计算机中对应字符串的最后一位)
当然,考虑字符串的头部为下标0的位置,即固定A,将B从右往左移动也是可以的,即上图的顺序是从右下到左上,下面考虑这种的代码实现。
实现示例
int LCString_Vio(string a, string b) {
// 稍微暴力一点的
int lena = a.length(), lenb = b.length();
int maxl = 0; // 最长长度
int i, j;
for (i = lena - 1; i >= 0; i--) {
int tmplen = 0; // 当前的最短距离
int iter = lena - 1 - i; // 当前递归的长度
if (iter > lenb - 1) iter = lenb - 1;
for (j = 0; j < iter; j++) {
tmplen += (a[i + j] == b[j]);
}
if (tmplen > maxl) maxl = tmplen;
}
return maxl;
}
此算法不需要动态规划数组来存储中间值,示例图来自 hackbuteer1的Blog
5.最小编辑距离
问题描述
编辑距离(Edit Distance),又称Levenshtein距离,是指两个字符串间,由一个转成另外一个所需的最少编辑操作次数。当然,允许的编辑只包括单个字符 替换、单个字符 插入和单个字符的 删除。一般来说,编辑距离越小,两个字符串的相似度越大。
例如将字符串 “kitten” 修改为 字符串"sitting" 则需要3次但字符编辑操作,如下:
- sitten ( k -> s )
- sittin (e -> i )
- sitting (_ -> g )
因此它们的编辑距离为3.
问题表示
为了定义子问题的状态,我们假设字符序列 A [ 1 , . . . , i ] A[1,...,i] A[1,...,i]、 B [ 1 , . . . , j ] B[1,...,j] B[1,...,j] 分别是字符串 A 和 B 的前i、j个字符组成的子串,由于在A中删除一个字符来匹配B,就相当于在B中插入一个字符来匹配A,即这两个操作可以相互转换,所以我们考虑只操作一个字符串,即固定字符串B,操作字符串A。
同时我们定义dp[i][j]是字符序列A[1,…,i]和B[1,…,j]的编辑距离,则有
-
插入操作

即 d p [ i ] [ j ] = d p [ i ] [ j − 1 ] + 1 dp[i][j] = dp[i][j-1] + 1 dp[i][j]=dp[i][j−1]+1 -
删除操作

即 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + 1 dp[i][j] = dp[i-1][j] + 1 dp[i][j]=dp[i−1][j]+1 -
修改操作

即 d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + 1 dp[i][j] = dp[i-1][j-1] + 1 dp[i][j]=dp[i−1][j−1]+1 -
不进行操作,

当然,对于不同的操作,我们可以赋予不同的权重。
所以,我们能得到动态递归方程:

其中, a i ≠ b j a_{i}≠b_{j} ai̸=bj 表示不相等时取1,相等时取0。字符串小标从1开始。
实现示例
/* 最小编辑距离 (Edit Distance) */
#include上述图源 BlackStorm的博客。
最小编辑距离在自然语言处理中可以用来度量两句话的相似程度【NLP_Stanford课堂】最小编辑距离。
后续
待补充。。。。