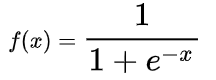全连接神经网络的原理及Python实现
作者:李小文,先后从事过数据分析、数据挖掘工作,主要开发语言是Python,现任一家小型互联网公司的算法工程师。
Github: https://github.com/tushushu
1. 原理篇
我们用人话而不是大段的数学公式来讲讲全连接神经网络是怎么一回事。
1.1 网络结构
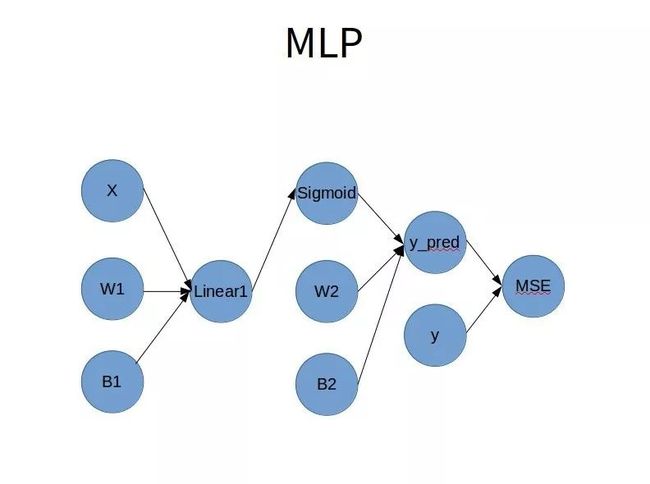
灵魂画师用PPT画个粗糙的网络结构图如下:
1.2 Simoid函数
Sigmoid函数的表达式是:
不难得出:
所以,Sigmoid函数的值域是(0, 1),导数为y * (1 - y)
1.3 链式求导
z = f(y)y = g(x)
dz / dy = f'(y)dy / dx = g'(x)
dz / dz = dz / dy * dy / dx = f'(y) * g'(x)
1.4 向前传播
将当前节点的所有输入执行当前节点的计算,作为当前节点的输出节点的输入。
1.5 反向传播
将当前节点的输出节点对当前节点的梯度损失,乘以当前节点对输入节点的偏导数,作为当前节点的输入节点的梯度损失。
1.6 拓扑排序
假设我们的神经网络中有k个节点,任意一个节点都有可能有多个输入,需要考虑节点执行的先后顺序,原则就是当前节点的输入节点全部执行之后,才可以执行当前节点。
2. 实现篇
本人用全宇宙最简单的编程语言——Python实现了全连接神经网络,便于学习和使用。简单说明一下实现过程,更详细的注释请参考本人github上的代码。
2.1 创建BaseNode抽象类
将BaseNode作为各种类型Node的父类。包括如下属性:
name -- 节点名称
value -- 节点数据
inbound_nodes -- 输入节点
outbound_nodes -- 输出节点
gradients -- 对于输入节点的梯度
class BaseNode(ABC):
def __init__(self, *inbound_nodes, name=None):
self.name = name
self._value = None
self.inbound_nodes = [x for x in inbound_nodes]
self.outbound_nodes = []
self.gradients = dict()
for node in self.inbound_nodes:
node.outbound_nodes.append(self)
def __str__(self):
size = str(self.value.shape) if self.value is not None else "null"
return "" % (self.name, size)
@property
def value(self)->ndarray:
return self._value
@value.setter
def value(self, value):
err_msg = "'value' has to be a number or a numpy array!"
assert isinstance(value, (ndarray, int, float)), err_msg
self._value = value
@abstractmethod
def forward(self):
return
@abstractmethod
def backward(self):
return
2.2 创建InputNode类
用于存储训练、测试数据。其中indexes属性用来存储每个Batch中的数据下标。
class InputNode(BaseNode):
def __init__(self, value: ndarray, name=None):
BaseNode.__init__(self, name=name)
self.value = value
self.indexes = None
@property
def value(self):
err_msg = "Indexes is None!"
assert self.indexes is not None, err_msg
return self._value[self.indexes]
@value.setter
def value(self, value: ndarray):
BaseNode.value.fset(self, value)
def forward(self):
return
def backward(self):
self.gradients = {self: 0}
for node in self.outbound_nodes:
self.gradients[self] += node.gradients[self]
2.3 创建LinearNode类
用于执行线性运算。
Y = WX + Bias
dY / dX = W
dY / dW = X
dY / dBias = 1
class LinearNode(BaseNode):
def __init__(self, data: BaseNode, weights: WeightNode, bias: WeightNode, name=None):
BaseNode.__init__(self, data, weights, bias, name=name)
def forward(self):
data, weights, bias = self.inbound_nodes
self.value = np.dot(data.value, weights.value) + bias.value
def backward(self):
data, weights, bias = self.inbound_nodes
self.gradients = {node: np.zeros_like(node.value) for node in self.inbound_nodes}
for node in self.outbound_nodes:
grad_cost = node.gradients[self]
self.gradients[data] += np.dot(grad_cost, weights.value.T)
self.gradients[weights] += np.dot(data.value.T, grad_cost)
self.gradients[bias] += np.sum(grad_cost, axis=0, keepdims=False)
2.4 创建MseNode类
用于计算预测值与实际值的差异。
MSE = (label - prediction) ^ 2 / n_label
dMSE / dLabel = 2 * (label - prediction) / n_label
dMSE / dPrediction = -2 * (label - prediction) / n_label
class MseNode(BaseNode):
def __init__(self, label: InputNode, pred: LinearNode, name=None):
BaseNode.__init__(self, label, pred, name=name)
self.n_label = None
self.diff = None
def forward(self):
label, pred = self.inbound_nodes
self.n_label = label.value.shape[0]
self.diff = (label.value - pred.value).reshape(-1, 1)
self.value = np.mean(self.diff**2)
def backward(self):
label, pred = self.inbound_nodes
self.gradients[label] = (2 / self.n_label) * self.diff
self.gradients[pred] = -self.gradients[label]
2.5 创建SigmoidNode类
用于计算Sigmoid值。
Y = 1 / (1 + e^(-X))
dY / dX = Y * (1 - Y)
class SigmoidNode(BaseNode):
def __init__(self, input_node: LinearNode, name=None):
BaseNode.__init__(self, input_node, name=name)
@staticmethod
def _sigmoid(arr: ndarray) -> ndarray:
return 1. / (1. + np.exp(-arr))
@staticmethod
def _derivative(arr: ndarray) -> ndarray:
return arr * (1 - arr)
def forward(self):
input_node = self.inbound_nodes[0]
self.value = self._sigmoid(input_node.value)
def backward(self):
input_node = self.inbound_nodes[0]
self.gradients = {input_node: np.zeros_like(input_node.value)}
for output_node in self.outbound_nodes:
grad_cost = output_node.gradients[self]
self.gradients[input_node] += self._derivative(self.value) * grad_cost
2.6 创建WeightNode类
用于存储、更新权重。
class WeightNode(BaseNode):
def __init__(self, shape: Union[Tuple[int, int], int], name=None, learning_rate=None):
BaseNode.__init__(self, name=name)
if isinstance(shape, int):
self.value = np.zeros(shape)
if isinstance(shape, tuple):
self.value = np.random.randn(*shape)
self.learning_rate = learning_rate
def forward(self):
pass
def backward(self):
self.gradients = {self: 0}
for node in self.outbound_nodes:
self.gradients[self] += node.gradients[self]
partial = self.gradients[self]
self.value -= partial * self.learning_rate
2.7 创建全连接神经网络类
class MLP:
def __init__(self):
self.nodes_sorted = []
self._learning_rate = None
self.data = None
self.prediction = None
self.label = None
2.8 网络结构
def __str__(self):
if not self.nodes_sorted:
return "Network has not be trained yet!"
print("Network informantion:\n")
ret = ["learning rate:", str(self._learning_rate), "\n"]
for node in self.nodes_sorted:
ret.append(node.name)
ret.append(str(node.value.shape))
ret.append("\n")
return " ".join(ret)
2.9 学习率
存储学习率,并赋值给所有权重节点。
@property
def learning_rate(self) -> float:
return self._learning_rate
@learning_rate.setter
def learning_rate(self, learning_rate):
self._learning_rate = learning_rate
for node in self.nodes_sorted:
if isinstance(node, WeightNode):
node.learning_rate = learning_rate
2.10 拓扑排序
实现拓扑排序,将节点按照更新顺序排列。
def topological_sort(self, input_nodes):
nodes_sorted = []
que = copy(input_nodes)
unique = set()
while que:
node = que.pop(0)
nodes_sorted.append(node)
unique.add(node)
for outbound_node in node.outbound_nodes:
if all(x in unique for x in outbound_node.inbound_nodes):
que.append(outbound_node)
self.nodes_sorted = nodes_sorted
2.11 前向传播和反向传播
def forward(self):
assert self.nodes_sorted is not None, "nodes_sorted is empty!"
for node in self.nodes_sorted:
node.forward()
def backward(self):
assert self.nodes_sorted is not None, "nodes_sorted is empty!"
for node in self.nodes_sorted[::-1]:
node.backward()
def forward_and_backward(self):
self.forward()
self.backward()
2.12 建立全连接神经网络
def build_network(self, data: ndarray, label: ndarray, n_hidden: int, n_feature: int):
weight_node1 = WeightNode(shape=(n_feature, n_hidden), name="W1")
bias_node1 = WeightNode(shape=n_hidden, name="b1")
weight_node2 = WeightNode(shape=(n_hidden, 1), name="W2")
bias_node2 = WeightNode(shape=1, name="b2")
self.data = InputNode(data, name="X")
self.label = InputNode(label, name="y")
linear_node1 = LinearNode(
self.data, weight_node1, bias_node1, name="l1")
sigmoid_node1 = SigmoidNode(linear_node1, name="s1")
self.prediction = LinearNode(
sigmoid_node1, weight_node2, bias_node2, name="prediction")
MseNode(self.label, self.prediction, name="mse")
input_nodes = [weight_node1, bias_node1,
weight_node2, bias_node2, self.data, self.label]
self.topological_sort(input_nodes)
2.13 训练模型
使用随机梯度下降训练模型。
def train_network(self, epochs: int, n_sample: int, batch_size: int, random_state: int):
steps_per_epoch = n_sample // batch_size
for i in range(epochs):
loss = 0
for _ in range(steps_per_epoch):
indexes = choice(n_sample, batch_size, replace=True)
self.data.indexes = indexes
self.label.indexes = indexes
self.forward_and_backward()
loss += self.nodes_sorted[-1].value
print("Epoch: {}, Loss: {:.3f}".format(i + 1, loss / steps_per_epoch))
print()
2.14 移除无用节点
模型训练结束后,将mse和label节点移除。
def pop_unused_nodes(self):
for _ in range(len(self.nodes_sorted)):
node = self.nodes_sorted.pop(0)
if node.name in ("mse", "y"):
continue
self.nodes_sorted.append(node)
2.15 训练模型
def fit(self, data: ndarray, label: ndarray, n_hidden: int, epochs: int,
batch_size: int, learning_rate: float):
label = label.reshape(-1, 1)
n_sample, n_feature = data.shape
self.build_network(data, label, n_hidden, n_feature)
self.learning_rate = learning_rate
print("Total number of samples = {}".format(n_sample))
self.train_network(epochs, n_sample, batch_size)
self.pop_unused_nodes()
def predict(self, data: ndarray) -> ndarray:
self.data.value = data
self.data.indexes = range(data.shape[0])
self.forward()
return self.prediction.value.flatten()
3 效果评估
3.1 main函数
使用著名的波士顿房价数据集,按照7:3的比例拆分为训练集和测试集,训练模型,并统计准确度。
@run_time
def main():
print("Tesing the performance of MLP....")
data, label = load_boston_house_prices()
data = min_max_scale(data)
data_train, data_test, label_train, label_test = train_test_split(
data, label, random_state=20)
reg = MLP()
reg.fit(data=data_train, label=label_train, n_hidden=8,
epochs=1000, batch_size=8, learning_rate=0.0008)
get_r2(reg, data_test, label_test)
print(reg)
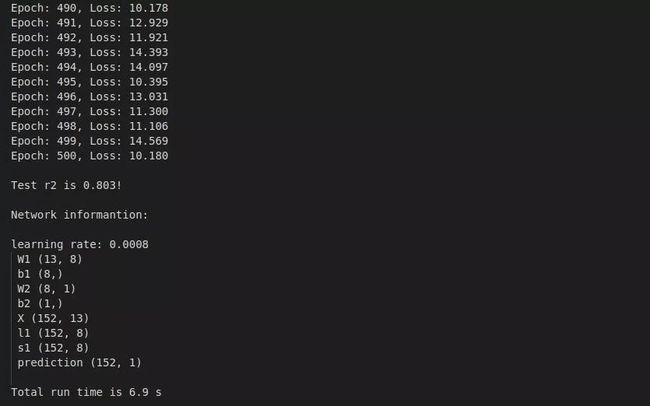
3.2 效果展示
拟合优度0.803,运行时间6.9秒。
3.3 工具函数
本人自定义了一些工具函数,可以在github上查看
https://github.com/tushushu/imylu/tree/master/imylu/utils
1、run_time - 测试函数运行时间2、load_boston_house_prices - 加载波士顿房价数据3、train_test_split - 拆分训练集、测试集4、get_r2 - 计算拟合优度
总结
矩阵乘法
▼ 点击成为社区注册会员 「在看」一下,一起PY