基于正则化的特征选择
此文写作尚不完整,有更深层需求的读者可参阅相关paper。
1、特征选择简述
降维,有时也可称为子空间学习,可以大致分为特征选择(feature selection)和特征提取(feature extraction)两大类,我们常说的主成分分析(PCA)、线性判别分析(LDA)、流形学习的代表—-局部线性嵌入(LLE)等,都是属于后者。特征提取,通常是将原始数据投影到一个新的空间,对于线性方法,就是学习一个投影矩阵W,使得投影后的数据最具有代表性信息(如PCA),或者最具有区分性信息(如LDA)。从特征的数值来看,特征提取会改变原始数值,相当于生成了新的通常来说是更好的特征。在一些实际应用中,比如生物医学中的基因分析,需要找到某一种疾病跟哪些基因有关系(通常只跟个别或少数几个基因有较大关联),或者在文本挖掘中,需要找到一些关键的字词,这个时候,我们就不能改变原始的特征数值,因此传统的特征提取不能直接派上用场。有需求,就有市场,特征选择的提出,正式为了解决这一类问题。通过设计一些准则,特征选择算法可以挑出原始特征中比较有用的特征子集,而不会改变原始特征数值。下面给个图直观看一下两者的区别。
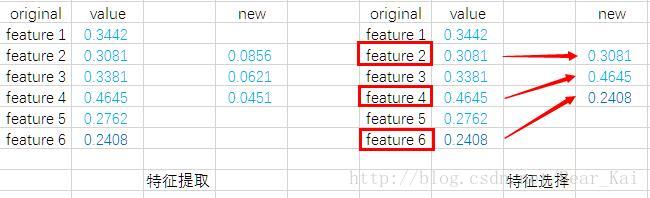
现有的特征选择算法,从不同的角度,可以分为不同的类型。按数据标签的获取情况,可以分为有监督、半监督和无监督特征选择;按是否需要额外的学习算法参与特征选择过程,以及具体的参与方式,可以分为封装型(wrapper)、嵌入式(embedded)和过滤型(filter)。再细致一些,可以分为基于信息论的特征选择、基于统计的特征选择、基于相似性的特征选择、基于稀疏学习的特征选择,等等。
上述提及的第一种分类方式,是机器学习中最为常见的,对于有监督/半监督方法利用标签的形式,有直接通过回归项引入标签信息,也有间接通过图来引入标签信息(即在构建图的过程中引入)。第二种分类方式,个人感觉在近年来,对某些方法的归属类别,不同学者开始出现一些分歧,原因可能跟近年来引起众多研究者关注的正则化技术有关,使得原本的界线划分变得比较模糊,不过也正说明,这种分类方式本身就没有一个很严格的定义,只是概念上的大致区分。最后提到的分类方式,是根据特征选择算法具体用到的准则/技术来划分,所以一种算法同时分属不同的类别也是可能的,我个人更乐意把这里所谓的类别名,称为某一算法的组成成分。在此篇博客中,我们主要关注基于正则化(regularization)的特征选择。
2、基于正则化的特征选择算法概览
先给出一些范数(norm)的定义和记法。向量 v∈Rn 的 ℓp -norm是 ∥v∥p=(∑ni=1|vi|p)1p ( p≠0 ), ℓ0 -norm是 ∥v∥0=∑ni=1|vi|0 (即 ℓ0 -norm是向量 v 中非零元素的个数)。矩阵 W∈Rd×m 的 ℓr,p -norm定义为 ∥W∥r,p=(∑di=1(∑mj=1|wij|r)pr)1p ( r≠0,p≠0 ),其中 ℓ2,2 -norm通常被称作F范数(Frobenius norm), ℓ2,0 -norm定义为 ∥W∥2,0=∑di=1∥∑mj=1w2ij∥0 。值得注意的是,这里 ℓ0 -norm和 ℓ2,0 -norm并不是真正有效的范数定义,因为它们不满足范数的齐次性:对常数 λ ,有 ∥λv∥0=|λ|∥v∥0 , ∥λW∥2,0=|λ|∥W∥2,0 。只不过为了表述的一致,这里仍用范数这一概念。
先入为主,来个总结强调:向量的 ℓ0 -norm是向量中非零元素的个数,矩阵的 ℓ2,0 -norm是矩阵的非零行的个数。特征选择任务直接引入这两个范数作为约束,好处是物理意义明确,我需要降到多少维(即选择多少特征),我就让非零元或非零行的个数为对应数值,这是个整数值,所以也方便调参,缺点是这两个范数会使目标式非凸,不利于优化求解。所以早期的算法中,通常是将这两个范数分别用 ℓ1 -norm和 ℓ2,1 -norm替代,一般作为正则项 引入,此两者虽然不具备特别明确的物理意义,但也具备使向量中的元素、矩阵中的行收缩(shrink)到0的功效,而且它们是凸的,便于优化求解。顺便提一句, ℓ1 -norm也被称作Lasso, ℓ2 -norm也被称作ridge回归, ℓ1 -norm和 ℓ2,1 -norm通常被用来获得鲁棒性或稀疏性。
下面旨在通过各目标函数,回顾各基于正则化的特征选择算法的主要思想,不涉及具体求解及优化细节,每小类仅选取4个代表方法,如前所述,这里的小类 可看作是算法的组成成分,所以一个算法可以同时属于多个小类,但本文中每个算法只在一个类中介绍。
2.1 基于回归
2.1.1 Lasso (1996)
Lasso 由Tibshirani于1996年提出,是一个带 ℓ1 -norm惩罚的回归问题,公式化表述如下:
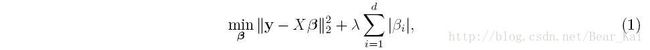
其中, β=[β1,…,βd]T∈Rd 是回归系数,求解上式等价于最小化第一项回归项,并带有这样一个约束: ∑di=1|βi|≤ϵ , ( ϵ>0 )。前已述及, ℓ1 -norm会使得向量 β 中的部分元素( λ 越大,为0/趋于0的元素越多)近似为0,我们可以将 β 中的元素的绝对值按从大到小的顺序排序,假如我们有6个特征,回归系数排完后是这样的: |β3|>|β4|>|β1|>|β2|>|β5|>|β6| ,回归系数绝对值越大,说明对应的特征越重要,所以,如果需要选择3个特征,自然就是第1、3、4号特征。
2.1.2 RFS (NIPS 2010)
RFS是一个有监督的特征选择方法,其目标函数为:
![]()
由于回归项采用了 ℓ2,1 -norm,所以RFS具有鲁棒特性,对回归系数矩阵W施加 ℓ2,1 -norm惩罚,使得W的部分行趋于零行,我们可以计算每一行的 ℓ2 -norm值,然后对这些值由大到小进行排序,选择 ℓ2 -norm值较大的行对应的特征。
2.1.3 ℓ2,0 -norm ALM (IJCAI 2013)
2.1.4 FSDL (AAAI 2014)
![]()
2.2 基于数据重构
2.2.1 CPFS (ICDM 2010)
2.2.2 RSR (PR 2015)
2.2.3 EUFS (AAAI 2015)
2.2.4 GRFS (TKDE 2015)
2.3 基于伪标签
2.3.1 JELSR (IJCAI 2011)
![]()
2.3.2 RUFS (IJCAI 2013)
![]()
2.3.3 RSFS (ICDM 2014)
![]()
2.3.4 AUFS (IJCNN 2015)
![]()
2.4 基于结构保持
2.4.1 LDFS (ICDM 2010)
2.4.2 FSSL (IJCAI 2011)
2.4.3 UDFS (IJCAI 2011)
2.4.4 SOGFS (AAAI 2016)
3、特征选择相关资源
1. scikit-feature feature selection repository
2. Robust feature selection:gene expression data.rar


