Kaggle:入门赛Tatanic(泰坦尼克号)84.21%带你冲进前2%
Kaggle:入门赛Tatanic(泰坦尼克号)84.21%带你冲进前2%
0. 前言
可能你和我一样是机器学习的入门者,或许看过吴恩达老师的课,或许看过李航的《统计方法》,或许看过周志华的《机器学习》。机器学习的武功心法牢记在心,人在江湖总是要与人过招的,有了心法就要练习。Kaggle的泰坦尼克号是一个经典的实战项目,我也是个新手拜读过多篇该项目的技术文章,走过很多弯路。故让我们一起走进今天这边基础教学,如有不对之处请拍砖指正,小生不胜感激。
1. 背景
《泰坦尼克号》的电影相比大家都已经看过,那么以这个背景的项目我们就不能忽略背景的意义。任何的数据都是在真实现实中产生的,我们要分析数据,挖掘数据中的关系,就不能脱离背景。通过阅读项目的介绍和结合背景的理解,我有这么几个思考:
(1)妇女和儿童先走,能否在数据中表现出来
(2)船是从英国出发,社会等级是否会有影响
(3)船舱所处的位置是否会有影响
带着一些问题和思考让我们进行下一步
2. 数据导入
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline,make_pipeline
from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier
from sklearn.feature_selection import SelectKBest
from sklearn import cross_validation, metrics
from sklearn.grid_search import GridSearchCV, RandomizedSearchCV
import warnings
warnings.filterwarnings('ignore')
train = pd.read_csv('train.csv',dtype={"Age": np.float64})
test = pd.read_csv('test.csv',dtype={"Age": np.float64})
PassengerId=test['PassengerId']
all_data = pd.concat([train, test], ignore_index = True)然后让我们看看数据的一些分析:
train_data.info()
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB 对训练数据的分析我们可以看到有12个属性,同理我们对测试数据集也进行同样的分析,我们可以看出Survived是需要我们在测试数据集给出的结果,1-存活,0-死亡。同时我们也注意到Embarked属性有少量缺失,Age属性缺失不多,而Cabin属性缺失的很多。对于缺失属性的处理我们在第四节给出解决方法。下面给出各个属性代表的含义:
在我们对数据有了基本的了解后,就要寻找数据与最后结果生存的关系了。首先可以分析单个属性与生存的关系,然后多个属性的结合与生存的关系。
3.1 单特征分析
3.1.1 性别与是否幸存的关系
按照我们背景里的介绍,女士与小孩先走。是否是这样呢,让我们一探究竟:
sns.barplot(x="Sex", y="Survived", data=train, palette='Set3')3.1.2 船舱等级与是否幸存的关系
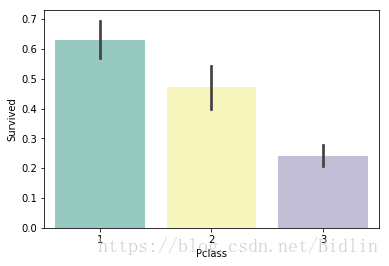
按照我们所想,船舱等级越高,人的身份可能越高。虽然灾难面前人与人之间是平等的,但是身份越高是否拥有特权呢,数据是不会说谎的:
sns.barplot(x="Pclass", y="Survived", data=train, palette='Set3')从上图我们可以看出,1,2,3舱的幸存率递减,1等舱的幸存率甚者是3等舱幸存率的3倍,灾难面前确实有些人存在优先权,各位看官多多挣钱吧。
3.1.3 年龄与幸存率的关系
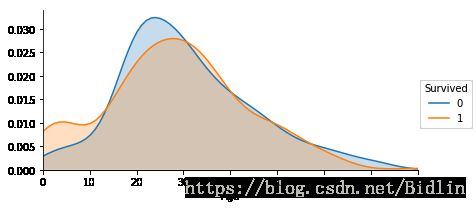
这个与咱们在3.1.1中说的一样,看下是否儿童能够获得更高的幸存率:
facet = sns.FacetGrid(train, hue="Survived",aspect=2)
facet.map(sns.kdeplot,'Age',shade= True)
facet.set(xlim=(0, train['Age'].max()))
facet.add_legend()从上面我们可以看出儿童的幸存比死亡高,而成年人大致上是死亡比幸存高。孩子是社会的未来,我们更应该好好的保护他们成长,而不是接二连三虐童和把刀子伸向手无寸铁的孩子们。
3.1.4 兄弟姐妹数与幸存率的关系
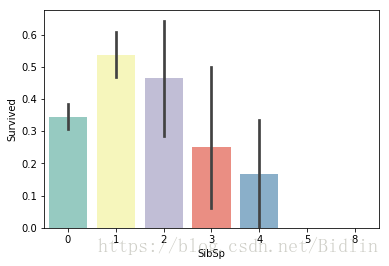
SibSp属性既然存在,兄弟姐妹数可能会间接体现这个家庭的生活水平,一家人出行兄弟姐妹多的很大概率就是儿童,能从侧面反应幸存率的问题:
sns.barplot(x="SibSp", y="Survived", data=train, palette='Set3')从图中我们能看出兄弟姐妹数为1,2的幸存率高,甚至比3,4的高一倍以上。
3.1.5 父母子女数是否与幸存有关系
在我们的印象中很少有儿童独自出远行(那个国家的家长也不放心),所以我猜测为0会是成年人,并且幸存率一定不高。父母子女数高的幸存率也不会高,灾难面前拖家带口的会照顾很多人,而且成年人也会把一丁点生的机会留给孩子和伴侣,人间的大爱不过如此,你说对不。下面就验证下咱们的猜测:
sns.barplot(x="Parch", y="Survived", data=train, palette='Set3')3.1.6 票价与幸存是否有关系
按照我们的经历,价位越高所处的位置就越好,可能社会地位就越高,可能也就更容易幸存。是否如此呢,让我们一起来看看。
首先我们来看下票价的信息:
train['Fare'].describe()count 891.000000
mean 32.204208
std 49.693429
min 0.000000
25% 7.910400
50% 14.454200
75% 31.000000
max 512.329200
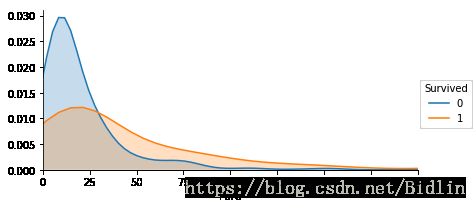
Name: Fare, dtype: float64facet = sns.FacetGrid(train, hue="Survived",aspect=2)
facet.map(sns.kdeplot,'Fare',shade= True)
facet.set(xlim=(0, 200))
facet.add_legend()我们可以看出大致随着票价的增长幸存比死亡高,有75%的票价不超过31,而这部分都是死亡率高于幸存率,而高于的幸存率都高过死亡率的。这说明票价与幸存是有一定相关性的。
3.1.7 船舱类型和幸存与否的关系
船舱有很多的缺失值,其实很不好分析。但是对于缺失值我们有这么几种分析思路:
(1)分为有值:1与缺失值:0进行对比分析
(2)缺失值填充字符,与其他一起进行分析
下面我们就用着2种思路进行分析一波,看看是否与幸存有关系。
对于第一种:
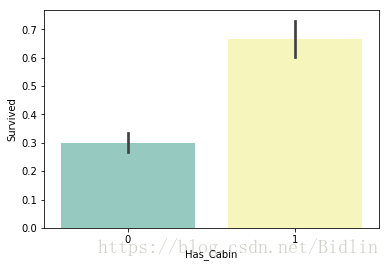
train.loc[train.Cabin.isnull(), 'Cabin'] = 'U0'
train['Has_Cabin'] = train['Cabin'].apply(lambda x: 0 if x == 'U0' else 1)
sns.barplot(x="Has_Cabin", y="Survived", data=train, palette='Set3')对于第二种思想:
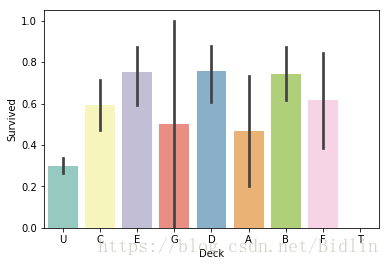
all_data['Cabin'] = all_data['Cabin'].fillna('Unknown')
all_data['Deck']=all_data['Cabin'].str.get(0)
sns.barplot(x="Deck", y="Survived", data=all_data, palette='Set3')3.1.8 称呼与幸存是否有关系
如果我们在日常英语的学习中,尤其是对英国文化了解的情况下,我们就会注意到对不同社会等级,不同年纪的人都会有不同的称呼。我们试着从Name特征中提取一些有用的信息。阅读了很多篇相关的文章,都会提取乘客的称呼,归纳分类。
all_data['Title'] = all_data['Name'].apply(lambda x:x.split(',')[1].split('.')[0].strip())
Title_Dict = {}
Title_Dict.update(dict.fromkeys(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer'))
Title_Dict.update(dict.fromkeys(['Don', 'Sir', 'the Countess', 'Dona', 'Lady'], 'Royalty'))
Title_Dict.update(dict.fromkeys(['Mme', 'Ms', 'Mrs'], 'Mrs'))
Title_Dict.update(dict.fromkeys(['Mlle', 'Miss'], 'Miss'))
Title_Dict.update(dict.fromkeys(['Mr'], 'Mr'))
Title_Dict.update(dict.fromkeys(['Master','Jonkheer'], 'Master'))
all_data['Title'] = all_data['Title'].map(Title_Dict)
sns.barplot(x="Title", y="Survived", data=all_data, palette='Set3')3.1.9 港口与幸存是否有关系
泰坦尼克号从英国的南安普顿港出发,途径法国瑟堡和爱尔兰昆士敦,如果是短途游客下船就不会遇难对吧。所以我们可以画个图看看:
sns.barplot(x="Embarked", y="Survived", data=train, palette='Set3')3.2 创造新特征
3.2.1 家庭人数与幸存是否有关系
我们在3.1中分析到兄弟姐妹特征,父母子女数可以生成一个新的特征:家庭人数。家庭人数也可以从侧面反映出一个家庭的经济状态,当然有一点我们不能忽略当家庭人员多的时候我们的行动都会受到限制需要照顾全家可能就会耽误最佳逃生时机。下面我们来分析看看是否如我们所想:
all_data['FamilySize']=all_data['SibSp']+all_data['Parch']+1
sns.barplot(x="FamilySize", y="Survived", data=all_data, palette='Set3')我们可以看到家庭人数为2,3,4的幸存率明显高于其他,当家庭人数为5,6,7我的猜测可能是需要照顾可能耽误最佳时机,哪怕有儿童。通过阅读其他文章,提供给我们一个新的思路:可以把家庭人数分为3类,生产新的数值特征便于分析。
def Fam_label(s):
if (s >= 2) & (s <= 4):
return 2
elif ((s > 4) & (s <= 7)) | (s == 1):
return 1
elif (s > 7):
return 0
all_data['FamilyLabel']=all_data['FamilySize'].apply(Fam_label)
sns.barplot(x="FamilyLabel", y="Survived", data=all_data, palette='Set3')3.2.2 票号相同数与幸存是否有关系
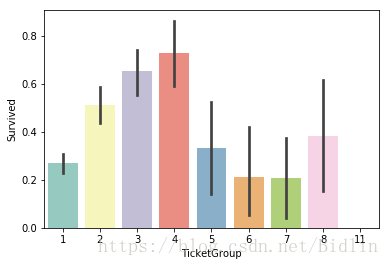
我们在3.1中分析了9个特征,还记得吗我们训练集有12个特征,其中1个Survived,1个PassengerId,我们漏掉了Ticket。因为发现有的票号是相同的,这提示我们有些可能是家庭票,那这样是否会和我们在3.2.1分析的家庭成员数为2,3,4的时候幸存率明显高于其他呢,让我们画个图来一看究竟:
Ticket_Count = dict(all_data['Ticket'].value_counts())
all_data['TicketGroup'] = all_data['Ticket'].apply(lambda x:Ticket_Count[x])
sns.barplot(x='TicketGroup', y='Survived', data=all_data, palette='Set3')3.3 思考
我们能否构造新的特征,新的分析方法,留给大家自己思考。
4. 数据清洗与缺失值填充
如果注意到我们上面的代码,你会发现我用了train,test,all_data,其中对一些特征的处理都是在all_data中处理的,这样我们一次就把训练集和测试集处理了。这里处理的方法我们借鉴于知乎:SweetWine的一些思路同时加上我的一些思考。
4.1 Age 特征填充
在上面的分析中我们得知Age属性缺失很多,看多很多填充的方法,有用平均数的,有用中位数的,这2种方法其实都没有考虑到每个乘客的不同属性,看似合理其实是最懒最不合理的。我们可以结合几个特征构造随机森林模型来填充Age。
from sklearn import cross_validation
train = all_data[all_data['Survived'].notnull()]
test = all_data[all_data['Survived'].isnull()]
# 分割数据,按照 训练数据:cv数据 = 1:1的比例
train_split_1, train_split_2 = cross_validation.train_test_split(train, test_size=0.5, random_state=0)
def predict_age_use_cross_validationg(df1,df2,dfTest):
age_df1 = df1[['Age', 'Pclass','Sex','Title']]
age_df1 = pd.get_dummies(age_df1)
age_df2 = df2[['Age', 'Pclass','Sex','Title']]
age_df2 = pd.get_dummies(age_df2)
known_age = age_df1[age_df1.Age.notnull()].as_matrix()
unknow_age_df1 = age_df1[age_df1.Age.isnull()].as_matrix()
unknown_age = age_df2[age_df2.Age.isnull()].as_matrix()
print (unknown_age.shape)
y = known_age[:, 0]
X = known_age[:, 1:]
rfr = RandomForestRegressor(random_state=0, n_estimators=100, n_jobs=-1)
rfr.fit(X, y)
predictedAges = rfr.predict(unknown_age[:, 1::])
df2.loc[ (df2.Age.isnull()), 'Age' ] = predictedAges
predictedAges = rfr.predict(unknow_age_df1[:,1::])
df1.loc[(df1.Age.isnull()),'Age'] = predictedAges
age_Test = dfTest[['Age', 'Pclass','Sex','Title']]
age_Test = pd.get_dummies(age_Test)
age_Tmp = df2[['Age', 'Pclass','Sex','Title']]
age_Tmp = pd.get_dummies(age_Tmp)
age_Tmp = pd.concat([age_Test[age_Test.Age.notnull()],age_Tmp])
known_age1 = age_Tmp.as_matrix()
unknown_age1 = age_Test[age_Test.Age.isnull()].as_matrix()
y = known_age1[:,0]
x = known_age1[:,1:]
rfr.fit(x, y)
predictedAges = rfr.predict(unknown_age1[:, 1:])
dfTest.loc[ (dfTest.Age.isnull()), 'Age' ] = predictedAges
return dfTest
t1 = train_split_1.copy()
t2 = train_split_2.copy()
tmp1 = test.copy()
t5 = predict_age_use_cross_validationg(t1,t2,tmp1)
t1 = pd.concat([t1,t2])
t3 = train_split_1.copy()
t4 = train_split_2.copy()
tmp2 = test.copy()
t6 = predict_age_use_cross_validationg(t4,t3,tmp2)
t3 = pd.concat([t3,t4])
train['Age'] = (t1['Age'] + t3['Age'])/2
test['Age'] = (t5['Age'] + t6['Age']) / 2
all_data = pd.concat([train,test])
print (train.describe())
print (test.describe())这里为什么这么处理呢,对训练集分为两半train1,train2,train1用作训练,然后填充train2的缺失值,然后用填充后的train2用来预测填充测试集。然后再来一次,这次用train2训练,train1填充。尽量降低对测试集的过拟合。
4.2 Embarked 特征填充
Embarkde特征缺失很少,我们看看都有哪些乘客。
all_data[all_data['Embarked'].isnull()]
我没看到只缺失2个,我们去找寻这2个缺失值的共性,Sex,Pclass,SliSp,Cabin,Fare特征都相同,并且Embarked为登船口,我们可以结合我们生活,做火车地点和票价Fare有着密切的联系。Pclass为1登陆口为C的用Fare为80.0,所以我们填充C。
all_data['Embarked'] = all_data['Embarked'].fillna('C')4.3 Fare 特征填充
Fare特征的缺失值也很少,我们同样可以利用几个相关的属性的中位数来填充,这里只给出代码:
fare=all_data[(all_data['Embarked'] == "S") & (all_data['Pclass'] == 3)].Fare.median()
all_data['Fare']=all_data['Fare'].fillna(fare)4.4 同组识别
这部分,原封不动的借鉴SweetWine分享的思路。
把姓氏相同的乘客划分为同一组,从人数大于一的组中分别提取出每组的妇女儿童和成年男性。
all_data['Surname']=all_data['Name'].apply(lambda x:x.split(',')[0].strip())
Surname_Count = dict(all_data['Surname'].value_counts())
all_data['FamilyGroup'] = all_data['Surname'].apply(lambda x:Surname_Count[x])
Female_Child_Group=all_data.loc[(all_data['FamilyGroup']>=2) & ((all_data['Age']<=12) | (all_data['Sex']=='female'))]
Male_Adult_Group=all_data.loc[(all_data['FamilyGroup']>=2) & (all_data['Age']>12) & (all_data['Sex']=='male')]发现绝大部分女性和儿童组的平均存活率都为1或0,即同组的女性和儿童要么全部幸存,要么全部遇难。
Female_Child=pd.DataFrame(Female_Child_Group.groupby('Surname')['Survived'].mean().value_counts())
Female_Child.columns=['GroupCount']
Female_ChildMale_Adult=pd.DataFrame(Male_Adult_Group.groupby('Surname')['Survived'].mean().value_counts())
Male_Adult.columns=['GroupCount']
Male_AdultFemale_Child_Group=Female_Child_Group.groupby('Surname')['Survived'].mean()
Dead_List=set(Female_Child_Group[Female_Child_Group.apply(lambda x:x==0)].index)
print(Dead_List)
Male_Adult_List=Male_Adult_Group.groupby('Surname')['Survived'].mean()
Survived_List=set(Male_Adult_List[Male_Adult_List.apply(lambda x:x==1)].index)
print(Survived_List)train=all_data.loc[all_data['Survived'].notnull()]
test=all_data.loc[all_data['Survived'].isnull()]
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Sex'] = 'male'
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Age'] = 60
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Title'] = 'Mr'
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Sex'] = 'female'
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Age'] = 5
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Title'] = 'Miss'4.5 特征转换
在这里我们把处理数值类型特征
all_data=pd.concat([train, test])
all_data=all_data[['Survived','Pclass','Sex','Age','Fare','Embarked','Title','FamilyLabel','Deck','TicketGroup']]
all_data=pd.get_dummies(all_data)
train=all_data[all_data['Survived'].notnull()]
test=all_data[all_data['Survived'].isnull()].drop('Survived',axis=1)
X = train.as_matrix()[:,1:]
y = train.as_matrix()[:,0]5. 模型选择与调参
5.1.1模型选择
随机森林有着众多优点,我们也对异常样本进行了惩罚不用担心过拟合的问题。当然GDBT,XGboost现在是数据挖掘比赛最常用的模型,但是面对这么小的数据量我还是建议用随机森林,或者说用简单的逻辑回归模型(需对票价和年龄进行缩放)。
5.2. 调参优化
pipe=Pipeline([('select',SelectKBest(k=20)),
('classify', RandomForestClassifier(random_state = 10, max_features = 'sqrt'))])
param_test = {'classify__n_estimators':list(range(20,50,2)),
'classify__max_depth':list(range(3,60,3))}
gsearch = GridSearchCV(estimator = pipe, param_grid = param_test, scoring='roc_auc', cv=10)
gsearch.fit(X,y)
print(gsearch.best_params_, gsearch.best_score_)5.3 预测提交
我们结合5.2节,不断的调整参数,然后预测提交获得更高的分数。
select = SelectKBest(k = 20)
clf = RandomForestClassifier(random_state = 10, warm_start = True,
n_estimators = 24,
max_depth = 6,
max_features = 'sqrt')
pipeline = make_pipeline(select, clf)
pipeline.fit(X, y)
predictions = pipeline.predict(test)
submission = pd.DataFrame({"PassengerId": PassengerId, "Survived": predictions.astype(np.int32)})
submission.to_csv("submission.csv", index=False)6. 总结
这是我取得的最高的分数,为了提高我也参阅很多资料比如Stacking框架进行模型融合。用RandomForest、AdaBoost、ExtraTrees、GBDT、DecisionTree、KNN、SVM 训练第一层。第二次XGBoost使用第一层预测的结果作为特征对最终的结果进行预测。结果被没有提高,可能是我第一层做模型融合这块,有很多需要注意的地方没有学习到,以后继续学习。最后还是很感谢我看过的每一份资料帮助我学到这么多东西,所以在我能提升的时候也把我所理解到的东西分享出来留给后续的学习者,如果你们能有所提升,请告诉我,万分感谢。
参考文章:
1. Kaggle Titanic 生存预测(Top1.4%)完整代码分享
2. Kaggle Titanic 生存预测 -- 详细流程吐血梳理
代码分享:
不留下代码就走的博主不是好博主:
1. CSDN下载页
2. Gtihub下载页
如果对你有帮助,在我的Github中点下Start,感谢。