超参数,判别生成模型,Metrics,梯度消失,正则化,VGG优点,dropout,GD和牛顿法,GD系列
1. 超参数和参数
参考这篇博客
参数是模型自己学习的部分,比如卷积核的weight以及bias
超参数是根据经验设定使得模型具有好的效果的参数,CNN中常见的超参数有:
1卷积层层数
2全连接层层数
3 卷积核size
4卷积核数目
5 learning rate
6正则化参数 λ \lambda λ
7minibatch size
8loss function
9weight initialization
10activation function
11 epochs
怎么样确定超参数呢?
我们将数据集分成训练集training set 验证集validation set和测试集 test set。在训练集上训练,用验证集来确定最好的超参数,然后用测试集来确定模型最终性能。
2.判别模型和生成模型
参考这篇博客
判别方法:由数据直接学习决策函数Y=f(X)或者条件概率分布P(Y|X)作为预测的模型,即判别模型。基本思想是有限样本条件下建立判别函数,不考虑样本的分布2模型,直接研究预测模型。典型的判别模型包括k近邻,感知级,决策树,支持向量机等。
特点:
不能反映训练数据本身的特性。但它寻找不同类别之间的最优分类面,反映的是异类数据之间的差异。直接面对预测,往往学习的准确率更高。由于直接学习P(Y|X)或P(X),可以对数据进行各种程度上的抽象、定义特征并使用特征,因此可以简化学习问题。
生成方法:由数据学习联合概率密度分布P(X,Y),然后求出条件概率分布P(Y|X)作为预测的模型,即生成模型:P(Y|X)= P(X,Y)/ P(X)。基本思想是首先建立样本的联合概率概率密度模型P(X,Y),然后再得到后验概率P(Y|X)。
特点:生成方法学习联合概率密度分布P(X,Y),所以就可以从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度。但它不关心到底划分各类的那个分类边界在哪。
3. 分类问题的Evaluation Metrics
参考这篇博客
对于一个分类器的好坏,主要是在测试集test set上表现出来的,衡量好坏的指标却不仅仅是accuracy。
accuracy的定义是 正 确 分 类 的 样 本 数 目 总 的 样 本 数 目 \frac{正确分类的样本数目}{总的样本数目} 总的样本数目正确分类的样本数目
我们先将我们关注的类定义为正类positive,不关注的定义为负类negative(是人或者不是)。
True Positive(TP):将正类判断为正类的样本个数
False Positive(FP):将负类判断为正类的样本个数
True Negative(TN):将负类判断为负类的样本个数
False Negative(FN):将正类判断为负类的样本个数
注意上述名字只需要记住第一个TP就能推断出后续名字含义了
精度Accuracy:
- A c c u r a c y = T P + T N T P + F P + T N + F N Accuracy=\frac{TP+TN}{TP+FP+TN+FN} Accuracy=TP+FP+TN+FNTP+TN
精确度Precision:
- P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
召回率Recall:
- R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
关于什么时候使用Precision和Recall,wiki上的解释是:
Precision: how many selected items are positive(对负样本的区分度)
Recall: how many positive items are selected(对正样本的区分度)
还有一个量度同时考虑了Recall和Precision,就是f1-measure
2 F 1 = 1 R + 1 P \frac{2}{F_1}=\frac{1}{R}+\frac{1}{P} F12=R1+P1
F1是R和P的调和平均数。
4. 梯度消失与梯度爆炸
这个应该从反向传播开始说起了,为了简便起见,来举一个cs231n中推倒反向传播的例子。

这里用的是一个两层网络的例子,两层的参数分别是 W 1 , W 2 W_1,W_2 W1,W2,这里假设的是y的label是0,所以最后的损失L就是 ∣ ∣ y ^ ∣ ∣ 2 ||\hat{y}||^2 ∣∣y^∣∣2,最终的反向传播是:
∂ L ∂ W 1 = ∂ L ∂ y ^ ∂ y ^ ∂ h 1 ∂ h 1 ∂ z 1 ∂ z 1 ∂ W 1 = x T y ^ ∗ W 2 T ∗ I [ h 1 > 0 ] \frac{\partial{L}}{\partial{W_1}}=\frac{\partial{L}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{h_1}}\frac{\partial{h_1}}{\partial{z_1}}\frac{\partial{z_1}}{\partial{W_1}}= x^T\hat{y}*W_2^T*I[h_1>0] ∂W1∂L=∂y^∂L∂h1∂y^∂z1∂h1∂W1∂z1=xTy^∗W2T∗I[h1>0]
可以看到这里是乘了ReLU的导数的,如果用的是其他激活函数,那么再多次乘以激活函数的导数之后,就会出现很小或者很大的梯度。
5. L1 L2 Regularization
参考这篇博客1
参考这篇博客2
L1和L2正则化是添加在loss function中避免overfitting的手段。
为什么加入正则化项可以避免过拟合呢?
一般从两个方面来解释 参考链接:
解释1 :
一个过拟合模型通常会去兼顾每一个训练数据点,因此在小区间范围内,函数值剧烈变化,意味着函数在某些小区间里的导数值非常大,因为变量总是有大有小,为了实现导数很大,只能通过添加大参数的方法。所以就加入L1或者L2正则项来约束参数大小。
解释2:
公式推倒链接
从贝叶斯的角度来分析, 正则化是为模型参数估计增加一个先验知识,先验知识会引导损失函数最小值过程朝着约束方向迭代。 L1正则是Laplace先验,L2是高斯先验。整个最优化问题可以看做是一个最大后验估计,其中正则化项对应后验估计中的先验信息,损失函数对应后验估计中的似然函数,两者的乘积即对应贝叶斯最大后验估计。
而拉普拉斯分布在乘以似然函数然后取对数之后,恰好转化成L1正则的形式,高斯分布同理转化成L2正则形式。
L1范数是指向量中各个元素绝对值之和,也叫“稀疏规则算子”(Lasso regularization,least absolute shrinkage and selection operator)。
一句话总结:L1范数和L0范数可以实现稀疏,L1因具有比L0更好的优化求解特性而被广泛应用,L2范数不具有实现稀疏的特性。
稀疏的优点:
1计算量上的优点
2可解释性,非零的特征提供了巨大的信息,使得我们不必要关心所以特征维度。
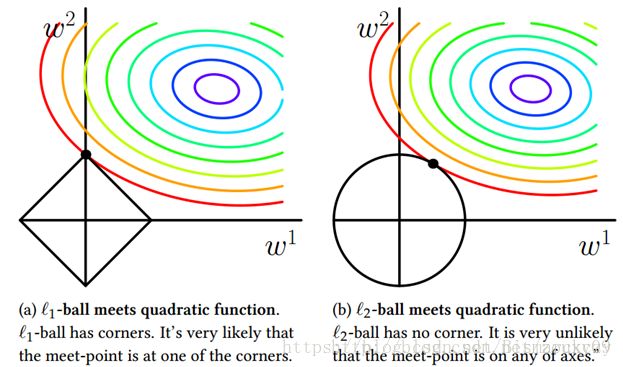
关于L1和L2在稀疏性上的区别可以参考下图,这里显示的是二维的情况,可以发现L1有大概率落在坐标轴上(为0),而L2不是。
当然数学上的解释可以参考博客1和2.
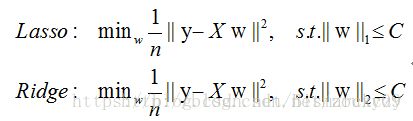
6 VGG的两个特点
第一个问题,为什么都使用3x3的小卷积核?

来看一下这张图,我们先看那个5x5的map,经过一个3x3卷积核之后,我们可以得到一个3x3的map,再经过一个3x3卷积核之后就只有一个1x1的map了,也就意味着这个这个1x1的map经过两个3x3的卷积核之后感受野receptive field是5x5,这和用一个5x5的卷积核是一样的效果。
但是两个3x3卷积核参数数目是18,小于5x5卷积核的25;
同样道理,三个串联的3x3卷积核感受野是7x7,但是参数是3x3x3,比7x7少很多。
更重要的是,3个串联的3x3卷积核会带来三次激活函数,引入了更多非线性变换,CNN对特征学习能力会更强。
第二个问题, 为什么让feature maps数目递增而不是每层一样多?
大家一般都是从直觉上回答(其实我觉得这个问题是一个很好的研究方向)。我来翻译一下quora上一个比较好的回答链接
逐层增加feature maps数目主要有两个原因。
1:因为我们使用pooling,会使得数据量变小(feature map变小,分辨率变低),那这样一来就可以通过增加feature map数目来专注于我们更关心的信息。
2:更深的层有更大的感受野,对应的通常是很高级的特征(比如浅层网络学习一条线,深层网络可能学到了一张脸),为了很好的捕捉并且区分开这些高级信息,我们增加feature maps数目来尽可能多的捕捉这些信息。
7 dropout实现
除了随机失活,提问者有时候更想听到的是伯努利分布。
首先应该从过拟合说起,网络层面防止过拟合主要有Batch Normalization(BN),Dropout,Regularization.
关于BN的解释在我另一篇博客Covariate shift and Batch ormalization里面,一句话总结起来就是说:internal covariate shift指的是神经网络每一层输入尺度和分布不一样,为了让模型快速学习并且收敛,我们把模型每一层输入都变成一个近似高斯分布,似乎很简单,对上一层layer A的输出减掉均值再除以标准差就可以输入到这一层layer B了,然而,神经网络是一个学习系统,这种粗暴的归一化会破坏layer A里面学好的模型,进入到layer B的参数不是最优了,为了优化模型,优化算法比如SGD对抵消undo掉我们之前做的normalization。
所以大佬们就引入了新的玩法,首先还是对layer A的输出做normalize,减掉均值,除以标准差,得到一个 x ^ \hat{x} x^, 然后引入两个learnable parameters γ , β \gamma,\beta γ,β:
x n e w = x ^ ∗ γ + β x_{new}=\hat{x}*\gamma+\beta xnew=x^∗γ+β
换句话说,优化算法你别改我上一层学好的weights了,就改这两个参数就行。
卧槽 BN这一句话有点长啊。回到Dropout。
先给出前向传播的例子
z l + 1 = w l + 1 ∗ y l + b l + 1 z^{l+1}=w^{l+1}*y^l+b^{l+1} zl+1=wl+1∗yl+bl+1
y l + 1 = f ( z l + 1 ) y^{l+1}=f(z^{l+1}) yl+1=f(zl+1), f是激活函数
如果对该层的输入y做一次dropout,
r = B e r n o u l l i ( p ) r=Bernoulli(p) r=Bernoulli(p) ,以概率p随机生成0,1向量
y ^ l = r ∗ y l \hat{y}^l=r*y^l y^l=r∗yl
z l + 1 = w l + 1 ∗ y ^ l + b l + 1 z^{l+1}=w^{l+1}*\hat{y}^l+b^{l+1} zl+1=wl+1∗y^l+bl+1
y l + 1 = f ( z l + 1 ) y^{l+1}=f(z^{l+1}) yl+1=f(zl+1), f是激活函数
为什么dropout能够解决过拟合:
因为不同的feature map学到了不同的特征,这些特征之间不是独立的,信息存在冗余,用dropout,使得特征之间尽可能独立,同时,每次更新的网络都是一个个相对独立的子网络,类似于集成学习。
8 简单总结一下优化方法
优化线性回归有三种方法,1求解析解,2梯度下降,3牛顿法
对于没有解析解的优化问题,用方法2和3。
博客1
博客2
博客3
这两种方法都是常见的求解极值问题的方法,而且都是通过迭代逼近的办法求得最优解。但是两者之间又有着千丝万缕的关系。对于梯度下降,梯度的步长是固定的。而对于牛顿法,步长是根据当前状态的导数或者二阶导数决定的,因此步长是动态变化的。但是因为这种动态的步长,使得牛顿法相比于梯度下降法,收敛速度会有所提高。但是用牛顿法求极值时,要求二阶导数存在,因此牛顿法的使用范围受到了一定的限制
此外还有拟牛顿法和各种牛顿法基础上的优化算法比如BFGS,L-BFGS。
9 梯度下降家族
相比于牛顿法,拟牛顿法等,神经网络的优化方法都是梯度下降方法,所以我还是先总结一下GD系列的方法吧。
文章来源 机器之心
一般的梯度下降GD是根据损失函数求学习参数的偏导数,也就是梯度,然后按照梯度的反方向来更新参数,更新由学习率learning rate来控制。
GD的主要三种变体是Batch GD, Stochastic GD, mini-batch GD。主要的不同就是每次用于计算目标函数的梯度的数据量不同。
BGD,每次用整个数据集求梯度。
缺点:速度慢,对大数据集失效,不能在线学习(运行中不能加新样本)
SGD,每次用一个样本计算梯度,可以在线学习。
缺点,噪声较多,并不是每次学习都往最优化方向进行。
MBGD,每次用m个样本计算梯度,速度较快,精度也较高。
缺点,两个主要的问题,一个是学习率的选择,第二个是陷入鞍点(不是极值点但是一阶导数为零的点)。
动量法 Momentum
该算法会考虑上一次的梯度,如果当前梯度与上一次的梯度方向一致,那么当前梯度会增强,反之梯度会减弱。
v t = γ v t − 1 + α ∇ ( θ ) v_t=\gamma v_{t-1}+\alpha\nabla(\theta) vt=γvt−1+α∇(θ)
θ = θ − v t \theta=\theta-v_t θ=θ−vt
Adaptive gradient (Adagrad)
Adagrad主要是对learning rate进行自动调整,设 θ t , i \theta_{t,i} θt,i是第t轮第i个参数
θ t + 1 , i = θ t , i − α G t , i i + e ∇ t , i \theta_{t+1,i}=\theta_{t,i}-\frac{\alpha}{\sqrt{G_{t,ii}+e}} \nabla_{t,i} θt+1,i=θt,i−Gt,ii+eα∇t,i
其中, G t ∈ R d × d G_t\in R^{d\times d} Gt∈Rd×d 为对角矩阵,每个对角线位置{i,i}为对应参数 θ i \theta_i θi从第1轮到第t轮梯度的平方和。e是平滑项,用于避免分母为0,一般取值1e−8。
Adagrad优点是对于对于出现频率较大的参数采取较小的学习率,对于出现频率较小的参数采取较大的学习率。
Adagrad的缺点是在训练的中后期,分母上梯度平方的累加将会越来越大,从而梯度趋近于0,使得训练提前结束。
RMSProp
为了解决Adagrad的问题,RMSProp不累加之前所有轮的梯度平方和,而仅仅计算之前梯度平方的均值。
E [ ∇ 2 ] t = 0.9 E [ ∇ 2 ] t − 1 + 0.1 ∇ t 2 E[\nabla^2]_t=0.9E[\nabla^2]_{t-1}+0.1\nabla_t^2 E[∇2]t=0.9E[∇2]t−1+0.1∇t2
θ t + 1 = θ t − α E [ ∇ 2 ] t + e ∇ t \theta_{t+1}=\theta_t-\frac{\alpha}{\sqrt{E[\nabla^2]_t+e}} \nabla_{t} θt+1=θt−E[∇2]t+eα∇t
自适应动量法Adaptive Momentum(Adam)
Adam可以说是Momentum方法和RMSProp方法的结合,不仅在
除了存储类似RMSprop 中指数衰减的过去梯度平方均值 外,Adam 法也存储像动量法中的指数衰减的过去梯度值均值 :