【机器学习笔记18】隐马尔可夫模型
【参考资料】
【1】《统计学习方法》
隐马尔可夫模型(HMM)定义
隐马尔可夫模型: 隐马尔可夫模型是关于时序的模型,描述一个由隐藏的马尔可夫链生成的不可观测的状态序列,再由各个状态生成的观测值所构成的一个观测序列。
形式化定义HMM为 λ = ( A , B , π ) \lambda = (A,B,\pi) λ=(A,B,π)
定义所有可能的状态值集合: Q = { q 1 , q 2 , . . . , q N } Q=\{q_1, q_2, ..., q_N \} Q={q1,q2,...,qN}
定义所有可能的观测值集合: V = { v 1 , v 2 , . . . , v M } V=\{v_1, v_2, ..., v_M \} V={v1,v2,...,vM}
定义长度为T的观测序列: I = ( i 1 , i 2 , . . . , i T ) I=(i_1, i_2, ..., i_T) I=(i1,i2,...,iT)
定义同样长度为T对应的状态序列: O = ( o 1 , o 2 , . . . , o T ) O=(o_1, o_2, ..., o_T) O=(o1,o2,...,oT)
定义状态转移矩阵,即状态序列的转移概率矩阵: A = [ a i j ] N × N A={[a_{ij}]}_{N \times N} A=[aij]N×N,其中 a i j = P ( i t + 1 = q j ∣ i t = q i ) a_{ij} = P(i_{t+1}=q_j|i_t=q_i) aij=P(it+1=qj∣it=qi)表示时刻t下状态为 q i q_i qi时,在t+1时刻状态迁移为 q j q_j qj的概率
定义观测概率矩阵: [ b j ( k ) ] N × M {[b_j(k)]}_{N \times M} [bj(k)]N×M,其中 b j ( k ) = P ( o t = v k ∣ i t = q j ) b_j(k)=P(o_t=v_k|i_t=q_j) bj(k)=P(ot=vk∣it=qj),表示在t时刻观测状态为 q j q_j qj时其隐藏的状态值为 v k v_k vk的概率
定义初始化状态概率为 π \pi π
HMM 存在两个基本假设
- 齐次马尔可夫性假设:
其观测值只依赖于前一时刻的观测值,与其他任何值无关,形式化表示如下
P ( i t ∣ i t − 1 , o t − 1 , . . . , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) P(i_t|i_{t-1},o_{t-1}, ..., i_1, o_1) = P(i_t|i_{t-1}) P(it∣it−1,ot−1,...,i1,o1)=P(it∣it−1)
- 观测独立性假设:
当前时刻的观测值只依赖与当前时刻的状态值,与其他任何值无关,形式化表示如下
P ( i t ∣ i t , o t , i t − 1 , o t − 1 , . . . , i 1 , o 1 ) = P ( i t ∣ o t ) P(i_t|i_t, o_t, i_{t-1},o_{t-1}, ..., i_1, o_1)=P(i_t|o_t) P(it∣it,ot,it−1,ot−1,...,i1,o1)=P(it∣ot)
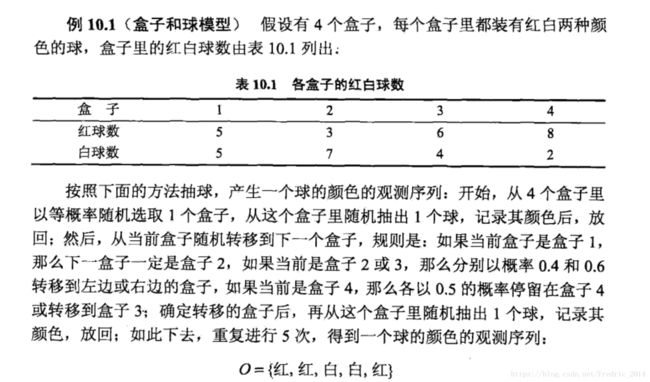
由上面这个例子,依次构建HMM模型得到:
Q={ 盒子1, 盒子2, 盒子3, 盒子4 }
V={ 红, 白 }
O={红, 红, 白, 白, 红}
π = ( 0.25 , 0.25 , 0.25 , 0.25 ) \pi = (0.25, 0.25, 0.25, 0.25 ) π=(0.25,0.25,0.25,0.25)
A = [ 0 1 0 0 0.4 0 0.6 0 0 0.4 0 0.6 0 0 0.5 0.5 ] A=\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0.4 & 0 & 0.6 & 0 \\ 0 & 0.4 & 0 & 0.6 \\ 0 & 0 & 0.5 & 0.5 \end{bmatrix} A=⎣⎢⎢⎡00.400100.4000.600.5000.60.5⎦⎥⎥⎤
B = [ 0.5 0.5 0.3 0.7 0.6 0.4 0.8 0.2 ] B=\begin{bmatrix} 0.5 & 0.5 \\ 0.3 & 0.7\\ 0.6 & 0.4\\ 0.8 & 0.2 \end{bmatrix} B=⎣⎢⎢⎡0.50.30.60.80.50.70.40.2⎦⎥⎥⎤
HMM的概率计算问题
问题描述: 给定模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = { o 1 , o 2 , . . . , o r } O=\{o_1, o_2, ..., o_r \} O={o1,o2,...,or},计算在模型 λ \lambda λ下观测序列O出现的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)
A.直接计算法
1.状态序列 I = { i 1 , i 2 , . . . , i r } I=\{ i_1, i_2, ..., i_r \} I={i1,i2,...,ir}产生的概率为 P ( I ∣ λ ) = π i 1 a i 1 i 2 a i 2 i 3 . . . a r − 1 r P(I|\lambda)=\pi_{i_1}a_{i_1i_2}a_{i_2i_3} ... a_{{r-1}r} P(I∣λ)=πi1ai1i2ai2i3...ar−1r,相当于从初始状态逐一生成后续的点,直到形成状态序列I。
2.对与上述生成的这个固定的状态序列 I = { i 1 , i 2 , . . . , i r } I=\{ i_1, i_2, ..., i_r \} I={i1,i2,...,ir},观测序列 O = { o 1 , o 2 , . . . , o r } O=\{o_1, o_2, ..., o_r \} O={o1,o2,...,or}为:
P ( O ∣ I , λ ) = b i 1 ( o 1 ) b i 2 ( o 2 ) . . . b i r ( o r ) P(O|I,\lambda)=b_{i_1}(o_1)b_{i_2}(o_2)...b_{i_r}(o_r) P(O∣I,λ)=bi1(o1)bi2(o2)...bir(or),即每个t时刻状态值生成对应观测值的概率。
3. O、I同时出现的概率 P ( O , I ∣ λ ) = P ( O ∣ I , λ ) P ( I ∣ λ ) = π i 1 b i 1 ( o 1 ) π i 2 b i 2 ( o 2 ) . . . π i r b i r ( o r ) P(O,I|\lambda)=P(O|I,\lambda)P(I|\lambda)=\pi_{i_1}b_{i_1}(o_1)\pi_{i_2}b_{i_2}(o_2)...\pi_{i_r}b_{i_r}(o_r) P(O,I∣λ)=P(O∣I,λ)P(I∣λ)=πi1bi1(o1)πi2bi2(o2)...πirbir(or)
4. 对所有可能的状态序列求观测序列的概率得到:
P ( O ∣ λ ) = ∑ I P ( O , I ∣ λ ) P(O|\lambda)=\sum\limits_{I}P(O,I|\lambda) P(O∣λ)=I∑P(O,I∣λ)
P ( O ∣ λ ) = ∑ I π i 1 b i 1 ( o 1 ) π i 2 b i 2 ( o 2 ) . . . π i r b i r ( o r ) P(O|\lambda)=\sum\limits_{I}\pi_{i_1}b_{i_1}(o_1)\pi_{i_2}b_{i_2}(o_2)...\pi_{i_r}b_{i_r}(o_r) P(O∣λ)=I∑πi1bi1(o1)πi2bi2(o2)...πirbir(or)
备注:这里SUM符号下标的I应该表示所有观测序列的排列组合,直接计算法计算量非常大,因此只用于理解算法,无实际操作可行
B.前向算法
前向概率定义: 给定模型 λ \lambda λ,定义到时刻t部分的观测序列为 o 1 , o 2 , . . . , o t o_1, o_2, ... , o_t o1,o2,...,ot,且状态为 q i q_i qi的概率为前向概率,计作:
a t ( i ) = P ( o 1 , o 2 , . . . , o t , i t = q i ∣ λ ) a_t(i)=P(o_1, o_2, ..., o_t, i_t=q_i|\lambda) at(i)=P(o1,o2,...,ot,it=qi∣λ)
- 初始值: a i ( i ) = π i b i ( o 1 ) , i = 1 , 2 , . . . , N a_i(i)=\pi_ib_i(o_1), \quad i=1,2,..., N ai(i)=πibi(o1),i=1,2,...,N
备注:表示在时刻t=1时,状态序列为 q i , . . , 1 N q_i,.., 1_N qi,..,1N下观测值为 o 1 o_1 o1的概率。
- 递推: t = 1 , 2 , . . . , T − 1 t=1,2,..., T-1 t=1,2,...,T−1
a t + 1 ( i ) = [ ∑ j = 1 N a t ( j ) a j i ] b i ( o t + 1 ) , i = 1 , 2 , . . . , N a_{t+1}(i)=[\sum\limits_{j=1}^{N}a_t(j)a_{ji}]b_i(o_{t+1}), \quad i=1,2,..., N at+1(i)=[j=1∑Nat(j)aji]bi(ot+1),i=1,2,...,N
备注:中括号里表示t时刻产生状态为 q i q_i qi的概率
- 终止: P ( O ∣ λ ) = ∑ i = 1 N a T ( i ) P(O|\lambda)=\sum\limits_{i=1}^{N}a_T(i) P(O∣λ)=i=1∑NaT(i)
备注:
第三步对理解非常中重要,是利用全概率的公式通过各个时刻的前向概率加出了总的概率,同时这种递推的计算大大减少了预算量,后向概率计算也类似。
HMM的学习问题
问题描述:已知观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1, o_2, ..., o_T) O=(o1,o2,...,oT),用极大似然估计(EM算法)来估计模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)。也就是使得 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)最大。
算法推导略
HMM的预测问题
问题描述:也称为解码问题,已知模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1, o_2, ..., o_T) O=(o1,o2,...,oT),求可能性最大的状态序列 I = ( i 1 , i 2 , . . . , i T ) I=(i_1, i_2, ..., i_T) I=(i1,i2,...,iT)
维特比算法 略
HMM 程序实现(基于hmmlearn)
# -*- coding: utf-8 -*-
import numpy as np
from hmmlearn import hmm
import warnings
def expand(a, b):
d = (b - a) * 0.05
return a-d, b+d
def _test_hmm_problem_01():
warnings.filterwarnings("ignore")
"""
HMM 解决概率计算问题
HMM 模型为lambda = (matric_a, matric_b, pi)
"""
state_list = ["box1", "box2", "box3", "box4"]
observ_list = ["red", "write"]
pi = [0.25, 0.25, 0.25, 0.25]
matric_a = np.array([
[0, 1, 0, 0],
[0.4, 0, 0.6, 0],
[0, 0.4, 0, 0.6],
[0, 0, 0.5, 0.5]
])
matric_b = np.array([
[0.5, 0.5],
[0.3, 0.7],
[0.6, 0.4,],
[0.8, 0.2]
])
model = hmm.MultinomialHMM(n_components=4)#状态的数量
model.startprob_ = pi
model.transmat_ = matric_a
model.emissionprob_ = matric_b
#观测序列为红、红、白、白、红
seen = np.array([[0, 0, 1, 1, 0]]).T
#score函数返回的是以自然对数为底的对数概率值
print(np.exp(model.score(seen))) #输出0.026862016
pass
def _test_hmm_problem_02():
warnings.filterwarnings("ignore")
"""
HMM 解决学习问题
"""
state_list = ["box1", "box2", "box3", "box4"]
observ_list = ["red", "write"]
model = hmm.MultinomialHMM(n_components=4, n_iter=100, tol=0.01)
sample = np.array([[0,1,0,1,1],[0,0,0,0,1],[1,1,0,1,1],[1,0,0,1,1]])
model.fit(sample)
#输出训练模型的初始值,状态转移和观测概率矩阵
print(model.startprob_)
print(model.transmat_)
print(model.emissionprob_)
pass
def _test_hmm_problem_03():
warnings.filterwarnings("ignore")
"""
HMM 解决预测问题
HMM 模型为lambda = (matric_a, matric_b, pi)
"""
state_list = ["box1", "box2", "box3", "box4"]
observ_list = ["red", "write"]
pi = [0.25, 0.25, 0.25, 0.25]
matric_a = np.array([
[0, 1, 0, 0],
[0.4, 0, 0.6, 0],
[0, 0.4, 0, 0.6],
[0, 0, 0.5, 0.5]
])
matric_b = np.array([
[0.5, 0.5],
[0.3, 0.7],
[0.6, 0.4,],
[0.8, 0.2]
])
model = hmm.MultinomialHMM(n_components=4)#状态的数量
model.startprob_ = pi
model.transmat_ = matric_a
model.emissionprob_ = matric_b
#观测序列为红、白、白、白、红
seen = np.array([[0, 1, 1, 1, 0]]).T
#score函数返回的是以自然对数为底的对数概率值
print(model.predict(seen)) #输出[0 1 0 1 2]
pass
"""
说明:
hmm代码实现,对应的笔记《隐马尔可夫模型》
以盒子模型为基础验证HMM模型的三个问题,概率计算、学习、预测(解码)
作者:fredric
日期:2018-9-20
"""
if __name__ == "__main__":
_test_hmm_problem_01()
_test_hmm_problem_02()
_test_hmm_problem_03()