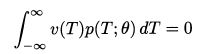估计——一般最小方差无偏估计
- 回顾
前面一直在讲述估计量的有效性(CRLB,线性模型),而没有提到假如估计量的方差没有达到CRLB,即是有效估计量不存在,但能够求出MVU估计量(假定存在)仍然是一个重要的事(可参考文章中的图片https://blog.csdn.net/GongPF/article/details/88715517)。因此,就提出了一般MVU估计。
- 主要使用的概念和方法
- 充分统计量(Sufficient statistic)
- RBLS定理(Rao-Blackwwell-Lehmann-Scheffe)
- 理解充分统计量
- 知乎:https://www.zhihu.com/question/41367707
- 一篇不知名的不知作者的文章描述:
- 这里举个例子:![]() , 估计参数
, 估计参数 ![]() ,w[n]是WGN,则可求出样本均值是MVU估计量
,w[n]是WGN,则可求出样本均值是MVU估计量
假设,这里选择 ![]() 作为估计量,那么可以看出
作为估计量,那么可以看出![]() 是无偏的,它的方差要比
是无偏的,它的方差要比![]() 大。 直观的理解:较差的性能是由于放弃了数据
大。 直观的理解:较差的性能是由于放弃了数据 ![]() 而导致的直接结果,这些信息携带了有关要估计参数
而导致的直接结果,这些信息携带了有关要估计参数![]() 的信息。
的信息。
这样就产生了这样的问题:哪些数据与估计问题(估计参数)有关?
- 对于上述关于![]() 估计问题,一旦知道了
估计问题,一旦知道了 ![\frac{1}{N}\sum_{n=0}^{N-1}x[n]](http://img.e-com-net.com/image/info8/3ce8961a18814326be141abdaa093953.gif) ,就不需要单个的数据值,因为关于参数
,就不需要单个的数据值,因为关于参数![]() 的所有的信息都已经包含在这个充分统计量中。详细解释如下:
的所有的信息都已经包含在这个充分统计量中。详细解释如下:
考虑数据的PDF为(需要估计A)
假定已经观测到统计量T(x)
这个统计量的知识将把数据的PDF改变为条件PDF,即
![]()
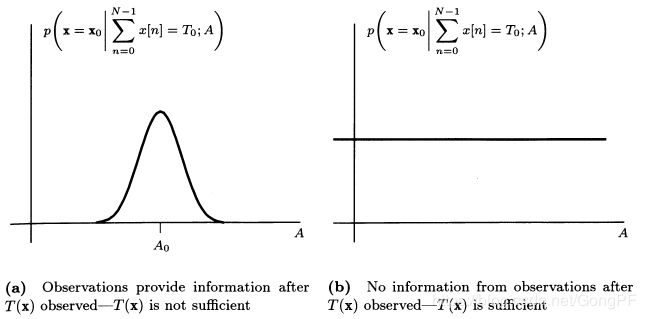
由于统计量是估计参数A的充分统计量,这个条件PDF就应该与估计参数 A 无关。因此,要证明统计量是充分的,就必须确认对应的条件PDF,并且确定它与估计参数无关。如下图所示:
计算条件PDF是比较难的事,所有需要一种更为简单的方法,下面就讲解Neyman-Fisher分解原理——一种寻找充分统计量的简单方法。
- Neyman-Fisher分解
- Neyman-Fisher 因子分解:若能将PDF ![]() 分解为
分解为
![]()
其中 g 只是通过 T(x) 才与 x 有关的函数;而 h 只是 x 的函数,那么 T(x) 是 ![]() 的充分统计量。反之,如果 T(x) 是
的充分统计量。反之,如果 T(x) 是 ![]() 的充分统计量,那么数据PDF
的充分统计量,那么数据PDF ![]() 可以分解为上式形式。
可以分解为上式形式。
例如:考虑 ![]() , 参数
, 参数 ![]() ,w[n]~N(0,
,w[n]~N(0,![]() ),但是参数
),但是参数 ![]() 为估计对象。假如数据PDF的N-F分解如下
为估计对象。假如数据PDF的N-F分解如下
- 联合充分统计量
- 定义:如果 m 个统计量![]() 的条件PDF
的条件PDF ![]() 与
与 ![]() 无关,那么这 m 个统计量联合充分统计量。
无关,那么这 m 个统计量联合充分统计量。
- N-F分解:如果![]() 能够分解为
能够分解为
![]()
那么![]() 是
是 ![]() 的充分统计量。很显然,原始数据总是充分统计量。
的充分统计量。很显然,原始数据总是充分统计量。
因为令m = N, ![]() 所有恒有g=p(x;
所有恒有g=p(x;![]() ) h=1 。
) h=1 。
- 利用充分统计量求MVU估计量(RBLS定理)
- 上面已经获取求 ![]() 的充分统计量T(x),那么就可以利用RBLS定理来求MVU估计量。
的充分统计量T(x),那么就可以利用RBLS定理来求MVU估计量。
- RBLS定理
如果 ![]() 是
是 ![]() 的无偏估计量,T(x) 是
的无偏估计量,T(x) 是 ![]() 的充分统计量,那么
的充分统计量,那么 ![]() 具有如下特性:
具有如下特性:
i)![]() 是
是 ![]() 的一个适用的估计量,即是与
的一个适用的估计量,即是与 ![]() 无关;
无关;
ii)![]() 是无偏的
是无偏的
iii)![]() 对于所有的
对于所有的 ![]() 来说,
来说,![]() 的方差要小于或等于
的方差要小于或等于 ![]() 的方差
的方差
iv)如果 T(x) 充分统计量是完备的,那么 ![]() 是MVU估计量
是MVU估计量
- 完备统计量(Completeness statistic)
定义1:a statistic that does not allow an unbiased estimator of zero.
定义2:从本质上来讲,如果只存在一个无偏统计量函数(统计量是样本的函数),那么该统计量就是完备的。
定义3:图来源:https://wenku.baidu.com/view/e3a2df49daef5ef7bb0d3c2e.html
充分完备统计量性质:对于某个参数 ![]() 的估计,假定充分统计量T(x)完备的,则存在唯一的函数 g 满足 E[g(T(x))] =
的估计,假定充分统计量T(x)完备的,则存在唯一的函数 g 满足 E[g(T(x))] = ![]() 。
。
更多性质参考:https://wenku.baidu.com/view/e3a2df49daef5ef7bb0d3c2e.html
总结完备性条件: 如果对于所有待估计参数 ![]() ,它的充分统计量 T 的任何一种构造函数 v(T) ,只对零函数即v(T)=0(对所有的T)满足下面条件
,它的充分统计量 T 的任何一种构造函数 v(T) ,只对零函数即v(T)=0(对所有的T)满足下面条件
那么,就说充分统计量是完备的。
- 解题思路(针对不知道MVU估计量时的参数估计问题)
1、利用R-F因子分解来求一个 估计参数 ![]() 的充分统计量 T(x)。
的充分统计量 T(x)。
2、确定充分统计量是否完备。如果是,继续往下处理;否者这个方法就不能使用。
3、求一个充分统计量的函数,以此来得到一个无偏估计量 ![]() 。那么,
。那么, ![]() 是MVU估计量。
是MVU估计量。
步骤3 可亦采用另一种方法
3‘、计算 ![]() ,其中
,其中 ![]() 是任意的无偏估计量。(实际中,条件期望计算复杂,视情况选择方法)
是任意的无偏估计量。(实际中,条件期望计算复杂,视情况选择方法)
![\hat{\theta }=\frac{1}{N}\sum_{n=0}^{N-1}x[n]](http://img.e-com-net.com/image/info8/07c21360198742bab6766158c37dfd49.gif)

![T(x)=\frac{1}{N}\sum_{n=0}^{N-1}x[n]=T_{0}](http://img.e-com-net.com/image/info8/f22c23f238fe4ca59ccdd64fa74845d7.gif)
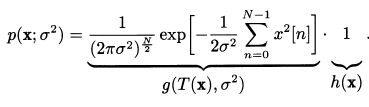
![T(x)=\sum_{n=0}^{N-1}x^{2}[n]](http://img.e-com-net.com/image/info8/1070966085294171ac4204ef42e7c03d.gif)