PageRank - 原理及代码解析

前言

因为最近要准备毕业设计了，论文设计到抽取句子中的关键词，要用到TextRank算法。而它是由PageRank改进而来的。

来源

搜索引擎中用到，用来进行网页重要性的排名。
谷歌创始人，斯坦福大学的佩奇和布林参考学术界对论文重要性的评判方法，引用次数越多说明约重要。
PageRank思想类似：

• 如果一个网页被其他很多网页链接，则重要，权值高。
• 如果PageRank值高的网页链接某个网页，则该网页权值也提高。

模型

将网页抽象成节点。举个例子，4个网页A,B,C,D。如图

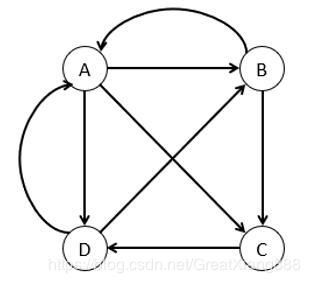
对于A来说，A指向B,C,D. 因为分成了3分，所以每条支路只能算1/3的权重。
输入形式采用json格式，如下：

{"A":["B","C","D"], "B":["A","C"], "C":["D"], "D":["A","B"]}

把上面的图写成转移矩阵M的形式：
$$M=\left[\begin{array}{cccc}A\to A& B\to A& C\to A& D\to A\\ A\to B& B\to B& C\to B& D\to B\\ A\to C& B\to C& C\to C& D\to C\\ A\to D& B\to D& C\to D& D\to D\end{array}\right]$$
对应这个例子M为：

    [[0.         0.5        0.         0.5       ]
     [0.33333333 0.         0.         0.5       ]
     [0.33333333 0.5        0.         0.        ]
     [0.33333333 0.         1.         0.        ]]

构建M矩阵代码：

def to_matrix(d):
    var = get_all_variables(d)
    n = len(var)
    # {'A': 0, 'B': 1, 'C': 2, 'D': 3}
    char2id = {var[i]:i for i in range(n)}
    M = np.zeros((n,n))
    # 构造M矩阵，先统计，后平均
    #[A->A  B->A  C->A  D->A]
    #[A->B  B->B  C->B  D->B] 等等
    # 统计
    for ch in var: #例如A
        for to in d[ch]: #["B","C","D"]
            y = char2id[ch]
            x = char2id[to]
            M[x][y] += 1
    '''M:
    [[0. 1. 0. 1.]
     [1. 0. 0. 1.]
     [1. 1. 0. 0.]
     [1. 0. 1. 0.]]
    '''
    #在列维度上取平均
    for j in range(n):
        sum1 = 0
        for i in range(n):
            sum1 += M[i][j]
        if sum1>0:
            for i in range(n):
                M[i][j] /= sum1
    '''M:
    [[0.         0.5        0.         0.5       ]
     [0.33333333 0.         0.         0.5       ]
     [0.33333333 0.5        0.         0.        ]
     [0.33333333 0.         1.         0.        ]]
    '''
    return np.matrix(M)

计算

初始权重为1/N
从上图可以看出，可以用矩阵的乘法来快速计算。

实验结果：

代码实现：

import json
import numpy as np
def to_matrix(d):
    var = get_all_variables(d)
    n = len(var)
    # {'A': 0, 'B': 1, 'C': 2, 'D': 3}
    char2id = {var[i]:i for i in range(n)}
    M = np.zeros((n,n))
    # 构造M矩阵，先统计，后平均
    #[A->A  B->A  C->A  D->A]
    #[A->B  B->B  C->B  D->B] 等等
    # 统计
    for ch in var: #例如A
        for to in d[ch]: #["B","C","D"]
            y = char2id[ch]
            x = char2id[to]
            M[x][y] += 1
    '''M:
    [[0. 1. 0. 1.]
     [1. 0. 0. 1.]
     [1. 1. 0. 0.]
     [1. 0. 1. 0.]]
    '''
    #在列维度上取平均
    for j in range(n):
        sum1 = 0
        for i in range(n):
            sum1 += M[i][j]
        if sum1>0:
            for i in range(n):
                M[i][j] /= sum1
    '''M:
    [[0.         0.5        0.         0.5       ]
     [0.33333333 0.         0.         0.5       ]
     [0.33333333 0.5        0.         0.        ]
     [0.33333333 0.         1.         0.        ]]
    '''
    return np.matrix(M)

def diedai(M, p):#迭代
    #矩阵相乘要用matmul，而不是multily
    #(4,4) * (4,1)
    return np.matmul(M,p)

def get_all_variables(d):
    s = set()
    #把所有元素加入集合中
    for k,v in d.items():
        s.add(k)
        for t in v:
            s.add(t)
    var = list(s)
    var.sort() #['A', 'B', 'C', 'D']
    return var

def page_rank(d,m):
    #迭代m次
    var = get_all_variables(d)
    M = to_matrix(d)
    tmp = 1.0/len(var)
    p = np.ones((len(var),1))*tmp
    p = np.matrix(p) #matrix可以直接p[0,0]这样取值
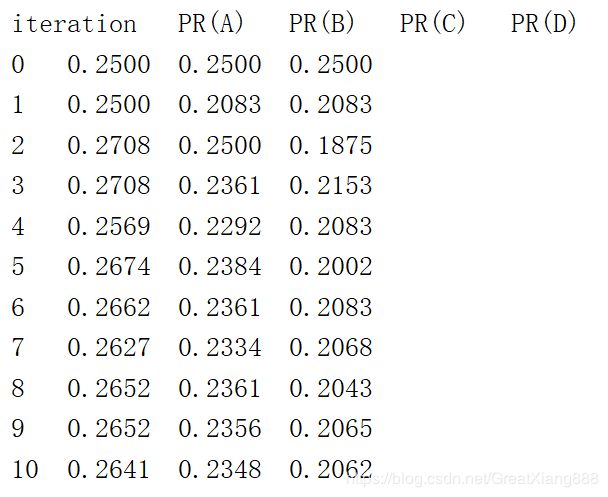
    print("iteration\tPR(A)\tPR(B)\tPR(C)\tPR(D)")
    print("{}\t{:.4f}\t{:.4f}\t{:.4f}\t".format(0,p[0,0],p[1,0],p[2,0],p[3,0]))
    for i in range(m):
        p = diedai(M,p) #用:.4f方式保留小数
        print("{}\t{:.4f}\t{:.4f}\t{:.4f}\t".format(i+1, p[0, 0], p[1, 0], p[2, 0], p[3, 0]))
    '''
    m=1时，p:
    [[0.25      ]
     [0.20833333]
     [0.20833333]
     [0.33333333]]
     '''
    return p


if __name__=="__main__":
    # str1 = input().strip()
    str1 = '''{"A":["B","C","D"], "B":["A","C"], "C":["D"], "D":["A","B"]}'''
    d = json.loads(str1)
    res = page_rank(d,10)

补充

这只是最简答的形式，实际上会做一个平滑处理：
d常取0.85，
$$PR(A)=(1-d)+d(\frac{PR(T_1))}{L(T_1))}+...+\frac{PR(T_n)}{L(T_n)})$$

参考：PageRank 笔记