编辑距离——莱文斯坦距离(Levenshtein distance)
在信息论和计算机科学中,莱文斯坦距离是一种两个字符串序列的距离度量。形式化地说,两个单词的莱文斯坦距离是一个单词变成另一个单词要求的最少单个字符编辑数量(如:删除、插入和替换)。莱文斯坦距离也被称做编辑距离,尽管它只是编辑距离的一种,与成对字符串比对紧密相关。
一、定义
数学上,两个字符串a、b之间的莱文斯坦距离,levab(|a|, |b|)
levab(i, j) = max(i, j) 如果min(i, j) = 0;
= min(levab(i - 1, j) + 1, levab(i, j-1) + 1, levab(i - 1, j - 1) + 1) (ai != bj) 否则
其中ai != bj 是指示函数,当ai != bj 是为1, 否则为0。注意在最小项:第一部分对应删除操作(从a到b)、第二部分对应插入操作、第三部分对应替换操作。
二、例子
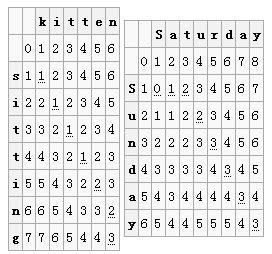
例如,“kitten”和”sitting”的编辑距离是3,因为按照如下需3个字符编辑从源字符串到目标字符串且没有比这种方式更少的编辑方式
1.kitten->sitten(用’s’取代‘k’)
2.sitten->sittin(用’i’取代’e’)
3.sittin->sitting(在末尾插入’g’)
三、上下界
莱文斯坦距离有几个简单的上下界,包括:
1.至少总是两个字符串大小的差值;
2.至多是较长字符串的长度;
3.当且仅当两个字符串相等时值为0;
4.如果两个字符串大小相等,汉明距离是其上界;
5.两个字符串的莱文斯坦距离不大于分别与第三个字符串的莱文斯坦距离之和(三角不等式)。
四、应用
在字符串近似匹配中,目标是从很多长的的文本中发现短文本的匹配,在这种情况下,较少差别的匹配是期望得到的。例如,短文本可以来自字典,这里,通常其中一个字符串是短的,另一个字符串是任意长的。莱文斯坦距离有着广泛的应用,例如,拼写检查、光学字符的校正系统、基于翻译记忆库的自然语言翻译的辅助软件。
五、与其他编辑距离度量的关系
其他的流行的编辑距离度量,包括了不同的编辑操作。例如
Damerau–莱文斯坦距离(Damerau–Levenshtein distance)允许插入、删除、替换和交换两个相邻字符;
最长公共子序列( longest common subsequence)只允许插入和删除操作;
汉明距离(Hamming distance)只允许替换操作,因此只适用于两个相等长度的字符串。
六、计算莱文斯坦距离
1、递归法
递归法计算莱文斯坦距离是直观但效率比较差,重复计算相同的子序列很多次,有效的改进方式是构造一个距离表存储每次计算的结果,最右下元素即为两个全字符串的levenshtein距离。
2.全矩阵迭代法
使用了自底向上的动态规划实现方法,也即上面提到的构造距离表取代重复计算相同子序列,相对于递归实现除速度显著改进外,算法运行时只需s_len * t_len的内存(s_len和t_len分别是字符串s和t的长度)
正确性证明:
算法的循环不变式是:可以转换初始的s[1…i]到t[1…j]使用最少的d[i, j]个操作,循环不变式得到保持的原因:
(1)初始的正确性:第0列,因为初始的部分s[1..i]可以通过简单的删除所有i个字符转换成空字符串t[1..0]。相似地,可以通过添加所有j个字符将空字符串s[1..0]转换成t[1..j]。
(2)如果s(i) = t(j),并且可以通过k个操作将s[1…i-1]转换成t[1..j-1]:可以对s[1..i-1]进行相同的操作,不对最后一个字符进行任何操作。
(3)否则,距离d[i, j]是三种可能转换方式中的最小距离:
(a)如果可以在k个操作中将s[1..i]转换成t[1..j-1],则可以在k+1个操作中通过简单的添加t[j]以得到t[1..j](插入操作);
(b)如果可以在k个操作中将s[1…i-1]转换成t[1…j],则可以在k+1个操作中移除s[i]之后做相同的转换(删除操作);
(c)如果可以在k个操作中将s[1…i-1]转换成t[1..j-1],可以对s[1..i]做相同的操作,之后交换原先的s[i]和t[j],总共k+1个操作(替换操作)。
将s[1…m]转换成t[1…n]所要求的操作理所当然的是转换s的所有字符到t的所有字符,所以d[m][n]是最终的结果。
这个证明并不能验证d[i][j]是实际的最小编辑距离,实际的证明过程比较困难,可以通过反证法进行证明。
3.两行迭代法
若不想重构已经被编辑的输入字符串,表明只要使用距离矩阵的两行即可计算莱文斯坦编辑距离(前一行和当前行)。
七、算法实现
在实现的过程中将三种实现方式作为一个源文件:
#include
int levenshteinDistance(char[], int, char[], int);
int levenshteinDynamicProgramming(char[], int, char[], int);
int levenshteinTwoRows(char[], int, char[], int);
int main()
{
char s[] = "sitting";
char t[] = "kitten";
int s_len = 7;
int t_len = 6;
int mindis;
mindis = levenshteinDistance(s, s_len, t, t_len);
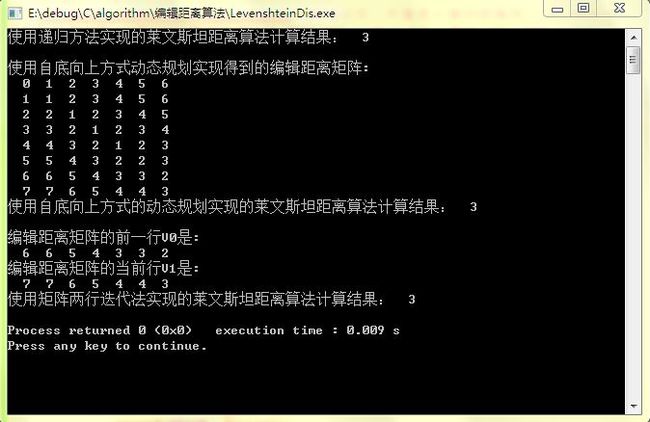
printf("使用递归方法实现的莱文斯坦距离算法计算结果:%3d\n\n", mindis);
mindis = levenshteinDynamicProgramming(s, s_len, t, t_len);
printf("使用自底向上方式的动态规划实现的莱文斯坦距离算法计算结果:%3d\n\n", mindis);
mindis = levenshteinTwoRows(s, s_len, t, t_len);
printf("使用矩阵两行迭代法实现的莱文斯坦距离算法计算结果:%3d\n", mindis);
return 0;
}
//求三个整数中的最小数
int Min(int x, int y, int z)
{
if(x <= y && x <= z)
return x;
else if (y <= z)
return y;
else
return z;
}
// levenshtein距离的递归实现
int levenshteinDistance(char s[], int s_len, char t[], int t_len)
{
int cost;
//基本情况,若字符串s和t的最小距离为0,则返回其中的最大距离作为编辑距离
if (s_len == 0)
return t_len;
if (t_len == 0)
return s_len;
//测试s和t的各自最后一个字符是否匹配
if (s[s_len - 1] == t[t_len - 1])
cost = 0;
else
cost = 1;
//使用公式,返回三者中的最小距离
return Min(levenshteinDistance(s, s_len - 1, t, t_len) + 1,
levenshteinDistance(s, s_len, t, t_len - 1) + 1,
levenshteinDistance(s, s_len - 1, t, t_len - 1) + cost
);
}
//levenshtein距离的自底向上方式的动态规划实现,把重复计算的距离存入一个矩阵中
int levenshteinDynamicProgramming(char s[], int s_len, char t[], int t_len)
{
//构建一个(s_len+1)*(t_len+1)的矩阵d,d[i][j]表示字符串s的前i字符和t的前j个字符的莱文斯坦距离
int d[s_len+1][t_len+1];
int i, j;
//源字符串s到空字符串t只要删除每个字符
for (i = 0; i <= s_len; i++)
d[i][0] = i;
//从空字符s到目标字符t只要添加每个字符
for (j = 1; j <= t_len; j++)
d[0][j] = j;
for (j = 0; j < t_len; j++)
for (i = 0; i < s_len; i++)
if (s[i] == t[j])
d[i+1][j+1] = d[i][j]; //不进行任何操作
else
d[i+1][j+1] = Min(d[i][j+1] + 1, //删除操作
d[i+1][j] + 1, //添加操作
d[i][j] + 1 //替换操作
);
printf("使用自底向上方式动态规划实现得到的编辑距离矩阵:\n");
for (i = 0; i <= s_len; i++) {
for (j = 0; j <= t_len; j++)
printf("%3d", d[i][j]);
printf("\n");
}
return d[s_len][t_len];
}
// evenshtein距离的两列矩阵的迭代实现
int levenshteinTwoRows(char s[], int s_len, char t[], int t_len)
{
//退化的基本情况
if (s_len == 0)
return t_len;
if (t_len == 0)
return s_len;
//构造两个工作向量,存放编辑距离的当前行和前一行
int v0[t_len + 1], v1[t_len + 1];
int i, j;
//初始化v0,即是A[0][i],从空字符串s到目标字符串t,只要添加每个字符
for (i = 0; i <= t_len; i++)
v0[i] = i;
for (i = 0; i < s_len; i++) {
//从前一行v0计算v1,v1的第一个元素是A[i+1][0],
//编辑距离就是从原字符串s中删除每个字符到目标字符串t
v1[0] = i + 1;
for (j = 0; j < t_len; j++) {
int cost = (s[i] == t[j]) ? 0:1;
v1[j + 1] = Min(v1[j] + 1, v0[j + 1] + 1, v0[j] + cost);
}
if (i == s_len - 1) {
printf("编辑距离矩阵的前一行V0是:\n");
for (j = 0; j <= t_len; j++)
printf("%3d", v0[j]);
printf("\n");
}
//为了下一次迭代,复制v1到v0
for (j = 0; j <= t_len; j++)
v0[j] = v1[j];
}
printf("编辑距离矩阵的当前行V1是:\n");
for (j = 0; j <= t_len; j++)
printf("%3d", v1[j]);
printf("\n");
return v1[t_len];
} 运行结果:
注:本文部分内容引用http://en.wikipedia.org/wiki/Levenshtein_distance更为详细的介绍可以参考英文维基百科原页面。
参考文献:
1·、https://blog.csdn.net/lhkaikai/article/details/25186255 2018.4.17