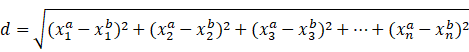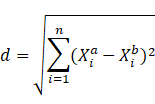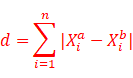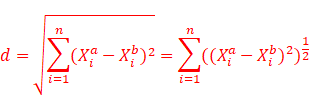机器学习算法 KNN（k-Nearest Neighbor）

目录

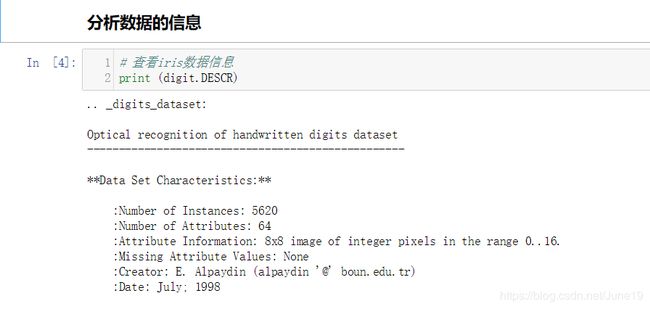
补充：超参数和模型参数

python实现：

KNN(K-Nearest Neighbors) K近邻算法 实现 手写 数据集的 分类问题

导入 手写数据集（digits）数据集

通过上面的分析，我们可以知道，怎么将现实中的东西以数据的形式表示

下面是 KNN 模型的 实例

step1：将数据切分为 训练集 和测试集

调用 sklearn 中的KNN算法

直接调用score，默认是计算精确度 accuracy

也可以调用sklearn中的accuracy来计算

很明显这个digits数据集获得的accuracy比 鸢尾花数据集要低，通过遍历来查找最优的K

考虑距离（权重），在sklearn中已经封装好了 是否 考虑距离这个参数，我们可以直接调用

考虑p

---

 

 

 

k近邻（k-Nearest Neighbor，简称KNN）学习是一种常用的监督学习算法，其工作机制非常简单：给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个“邻居”的信息来进行预测。通常，在分类任务中可使用“投票法”，即选择这k个样本中出现最多的类别标记作为预测结果；在回归任务中可使用“平均法”，即将这k个样本的实值输出标记的平均值作为预测结果；还可以基于距离远近进行加权平均或加权投票，距离越近的样本权重越大。

与前面介绍的学习方法相比，k近邻学习有一个明显的不同之处：它似乎没有显式的训练过程，。事实上，它是“懒惰学习（lazy learning）”的著名代表，此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为零，待收到测试样本后再进行处理；相应的，那些在训练阶段就对样本进行学习处理的方法，称为“急切学习（eager learning）”。

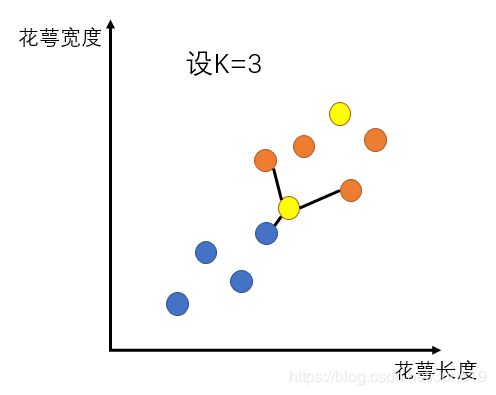
下面通过一个简单的例子来说明：

K设成3意思是找到离这个黄点最近的3个点，此时橙：蓝=2：1，故黄色点是橙色的。那么该怎么去计算这个距离呢？

二维空间点到点的距离公式(欧氏距离)：

d=(x1a-x1b)2+(y2a-y2b)2

a 和 b 是 样本，也就是行

1,2,3…n,是特征，也就是列

高维空间点到点的距离公式(欧氏距离)：

 

用矩阵的形式来

 

虽然橙色的离黄色近的有两个，但离蓝色的最近。

所以，这就涉及到权重的问题了。

这个权重也十分简单：它就是距离的倒数。

理解起来也很容易，距离越长，它的权重就越小，反之越大。

这样我们重新计算一下黄色究竟属于哪个类？

橙色：蓝色=

黄色小球属于蓝色

现在我们需要改变的两个超参数K和是否考虑距离。

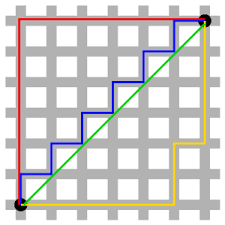
曼哈顿距离：

 

通过上面两个公式可以推出看出公式右上角的变化，这就是明可夫斯基距离：

d=i=1n((Xia-Xib)p)1p

这个p就是KNN算法的第三个超参数

可以看出红蓝黄线的长度是一样的

补充：超参数和模型参数

• 模型参数：模型运行过程中需要学习的参数
  • 人造神经网络中的权重。
  • 支持向量机中的支持向量。
  • 线性回归或逻辑回归中的系数
• 超参数(hyper-parameters)：人为外部设置的参数
  • 学习率 learning
  • Epoch
  • Step
  • Batch size
  • KNN 中的K，P，是否考虑距离权重
• 对KNN算法的思想总结一下：就是在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：
• 1）计算测试数据与各个训练数据之间的距离；
• 2）按照距离的递增关系进行排序；
• 3）选取距离最小的K个点；
• 4）确定前K个点所在类别的出现频率；
• 5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

python实现：

KNN(K-Nearest Neighbors) K近邻算法 实现 手写 数据集的 分类问题

import numpy as np

from sklearn import datasets # 导入 sklearn 已有的数据集

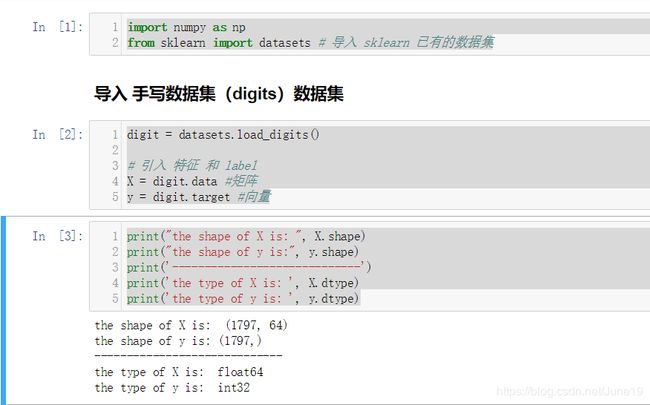
导入 手写数据集（digits）数据集

digit = datasets.load_digits()

 

# 引入 特征 和 label

X = digit.data #矩阵

y = digit.target #向量

 

print("the shape of X is: ", X.shape)

print("the shape of y is:", y.shape)

print('-----------------------------')

print('the type of X is: ', X.dtype)

print('the type of y is: ', y.dtype)

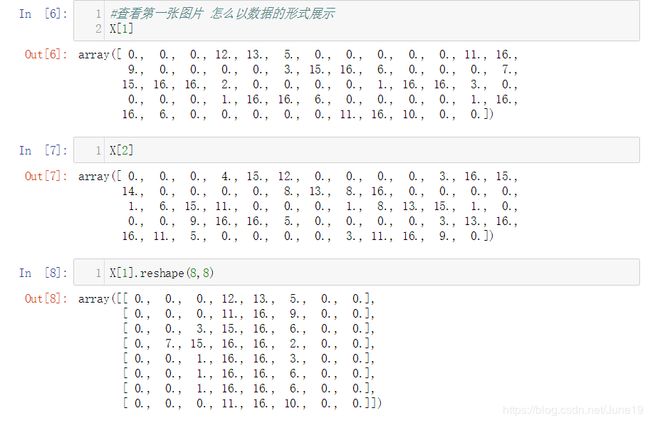
# 可视化 第一张图片的样子

import matplotlib.pyplot as plt

import matplotlib

 

digit_image = X[1].reshape(8,8) #这里要将64维的图片转为（8,8）的图片

plt.imshow(digit_image,cmap=matplotlib.cm.binary)

plt.show()

通过上面的分析，我们可以知道，怎么将现实中的东西以数据的形式表示

下面是 KNN 模型的 实例

step1：将数据切分为 训练集 和测试集

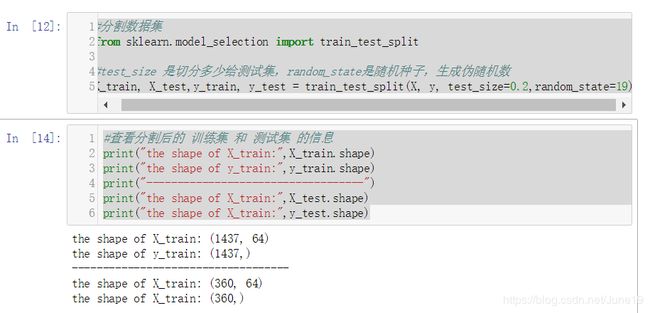
#分割数据集

from sklearn.model_selection import train_test_split

 

#test_size 是切分多少给测试集，random_state是随机种子，生成伪随机数

X_train, X_test,y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=19)

#查看分割后的 训练集 和 测试集 的信息

print("the shape of X_train:",X_train.shape)

print("the shape of y_train:",y_train.shape)

print("-----------------------------------")

print("the shape of X_train:",X_test.shape)

print("the shape of X_train:",y_test.shape)

 

调用 sklearn 中的KNN算法

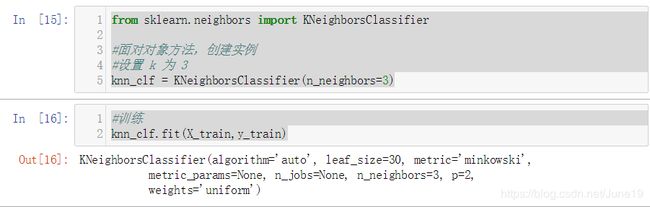
from sklearn.neighbors import KNeighborsClassifier

 

#面对对象方法，创建实例

#设置 k 为 3

knn_clf = KNeighborsClassifier(n_neighbors=3)

#训练

knn_clf.fit(X_train,y_train)

直接调用score，默认是计算精确度 accuracy

也可以调用sklearn中的accuracy来计算

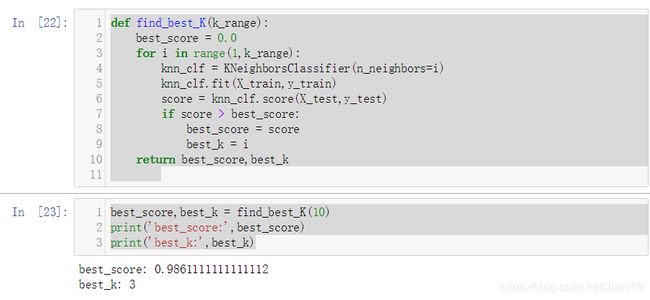
很明显这个digits数据集获得的accuracy比 鸢尾花数据集要低，通过遍历来查找最优的K

def find_best_K(k_range):

    best_score = 0.0

    for i in range(1,k_range):

        knn_clf = KNeighborsClassifier(n_neighbors=i)

        knn_clf.fit(X_train,y_train)

        score = knn_clf.score(X_test,y_test)

        if score > best_score:

            best_score = score

            best_k = i

    return best_score,best_k

best_score,best_k = find_best_K(10)

print('best_score:',best_score)

print('best_k:',best_k)

 

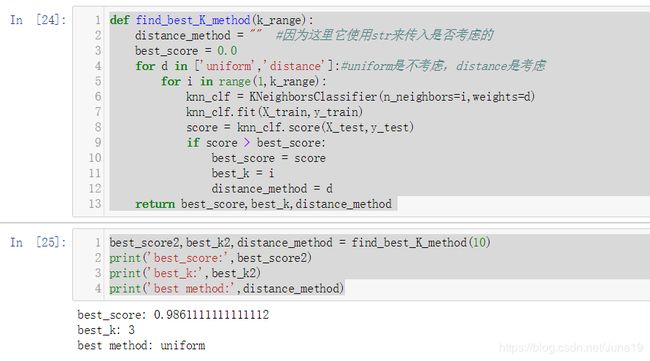
考虑距离（权重），在sklearn中已经封装好了 是否 考虑距离这个参数，我们可以直接调用

def find_best_K_method(k_range):

    distance_method = ""  #因为这里它使用str来传入是否考虑的

    best_score = 0.0

    for d in ['uniform','distance']:#uniform是不考虑，distance是考虑

        for i in range(1,k_range):

            knn_clf = KNeighborsClassifier(n_neighbors=i,weights=d)

            knn_clf.fit(X_train,y_train)

            score = knn_clf.score(X_test,y_test)

            if score > best_score:

                best_score = score

                best_k = i

                distance_method = d

return best_score,best_k,distance_method

best_score2,best_k2,distance_method = find_best_K_method(10)

print('best_score:',best_score2)

print('best_k:',best_k2)

print('best method:',distance_method)

考虑p

def find_best_K_method_p(k_range,ps):

    distance_method = "" #因为这里它使用str来传入是否考虑的

    best_score = 0.0

    best_p = 0.0

    for p in range(1,ps):

        for d in ['uniform','distance']:   #uniform 是不考虑， distance 是考虑

            for i in range(1,k_range):

                knn_clf = KNeighborsClassifier(n_neighbors=i, weights=d, p=p)

                knn_clf.fit(X_train,y_train)

                score = knn_clf.score(X_test,y_test)

                if score > best_score:

                    best_score = score

                    best_k = i

                    distance_method = d

                    best_p = p

return best_score,best_k,distance_method,best_p

best_score2, best_k2, distance_method, best_p = find_best_K_method_p(10,4)

print('best_score:', best_score2)

print('best K:', best_k2)

print('best method:', distance_method)

print('best p:', best_p)