1. 相关性的描述问题
独立性说明两者之间无关系,相关性可以说明两者之间有关系,但这两者之间关系强弱如何度量?我们可以有线性相关系数(皮尔逊积矩相关系数)、卡方检验(此处不谈)和互信息这几个指标来进行量化。
使用线性相关系数的前提自变量与因变量是线性关系,取值范围为[-1,1],负数表示负相关:
ρx,y=cov(X,Y)σX,σY=E[(X−uX)(Y−uY)]σX,σY ρ x , y = c o v ( X , Y ) σ X , σ Y = E [ ( X − u X ) ( Y − u Y ) ] σ X , σ Y
即协方差除以标准差的积。
而互信息是基于信息熵,适用面更广。
2. 信息熵与互信息
2.1 信息熵
信息熵表示要把一个事物弄清楚所需要的信息量的多少。所以,严格意义上来说,熵是表示不确定程度的度量,而非信息量的度量。意思是,熵小的,预测起来更容易。举个例子:一个汉字信息熵大约为8比特,英文的信息熵为4比特,意思是一个汉字所要表达意思的不确定度要大于英文,这说明了英文确实在很多方面表达精确度胜于汉字,因为更容易理解、预测它的意思。相应的,汉字存储压缩度更高,对应的英文原著翻译为中文版往往变薄了许多。
香农指出了信息熵必须满足费复兴,单调性,可加性这三种性质,并给出满足这三条性质的一种定义(当然也是目前唯一大家都用的定义):
H(X)=−∫XP(X)log(P(X)) H ( X ) = − ∫ X P ( X ) l o g ( P ( X ) )
P(X)是X的出现概率,即X分布越离散,X的状态数越多,信息熵越大。
#### 2.2 互信息:
互信息度量知道X,Y这两个变量其中一个,对另一个不确定度减少的程度,其定义为
I(X,Y)=∫x∫yP(X,Y)logP(X,Y)P(X)P(Y)=E(ln(P(X,Y)P(X)P(Y))) I ( X , Y ) = ∫ x ∫ y P ( X , Y ) l o g P ( X , Y ) P ( X ) P ( Y ) = E ( l n ( P ( X , Y ) P ( X ) P ( Y ) ) )
P(X)是X的出现概率,P(X,Y)是X,Y的联合概率概率
我们可以对以上进行变形:
I(X,Y)=∫x∫yP(X,Y)logP(X,Y)P(X)−∫X∫YP(X,Y)logP(Y)=∫X∫YP(X,Y)logP(Y|X)−∫X∫YP(X,Y)logP(Y)=∫X∫YP(Y|X)P(X)logP(Y|X)−∫X∫YP(X,Y)logP(Y)=∫XP(X)∫YP(Y|X)logP(Y|X)−∫XP(X,Y)∫YlogP(Y)=−∫XP(X)H(Y|X=x)−P(Y)∫YlogP(Y)=−∫XP(X)H(Y|X=x)−∫YP(Y)logP(Y)=−H(Y|X)+H(Y)=H(Y)−H(Y|X) I ( X , Y ) = ∫ x ∫ y P ( X , Y ) l o g P ( X , Y ) P ( X ) − ∫ X ∫ Y P ( X , Y ) l o g P ( Y ) = ∫ X ∫ Y P ( X , Y ) l o g P ( Y | X ) − ∫ X ∫ Y P ( X , Y ) l o g P ( Y ) = ∫ X ∫ Y P ( Y | X ) P ( X ) l o g P ( Y | X ) − ∫ X ∫ Y P ( X , Y ) l o g P ( Y ) = ∫ X P ( X ) ∫ Y P ( Y | X ) l o g P ( Y | X ) − ∫ X P ( X , Y ) ∫ Y l o g P ( Y ) = − ∫ X P ( X ) H ( Y | X = x ) − P ( Y ) ∫ Y l o g P ( Y ) = − ∫ X P ( X ) H ( Y | X = x ) − ∫ Y P ( Y ) l o g P ( Y ) = − H ( Y | X ) + H ( Y ) = H ( Y ) − H ( Y | X )
同理可得:
I(X,Y)=H(X)−H(X|Y) I ( X , Y ) = H ( X ) − H ( X | Y )
I(X,Y)=H(X,Y)−H(X|Y)−H(Y|X) I ( X , Y ) = H ( X , Y ) − H ( X | Y ) − H ( Y | X )
I(X,Y)=H(X)+H(Y)−H(X,Y) I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y )
a. 由上一行可以得出:互信息可以看作是X,Y两信息熵的交集
其图示如下:
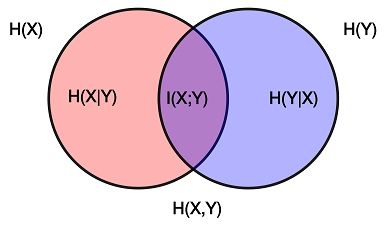
b. 互信息没有数值上的最大最小的界限,但可以依据A,B的互信息与A,B的信息熵相对大小,即用归一化的互信息,来量化A、B的关系强弱,比如常见的归一化方法:
I‘(X,Y)=2⋅I(X,Y)H(X)+H(Y) I ‘ ( X , Y ) = 2 ⋅ I ( X , Y ) H ( X ) + H ( Y )
I‘(X,Y)=I(X,Y)min(H(X),H(Y)) I ‘ ( X , Y ) = I ( X , Y ) m i n ( H ( X ) , H ( Y ) )
I‘(X,Y)=I(X,Y)sqrt(H(X)⋅H(Y)) I ‘ ( X , Y ) = I ( X , Y ) s q r t ( H ( X ) ⋅ H ( Y ) )
c. X,Y完全相关(比如完全线性相关)时,即X,Y之间满足一个函数映射关系,已知X,Y中一个则可以推导出另一个的所有状态及其概率,X,Y互信息最大,此时I(X,Y) = H(X) = H(Y)。
d. 当X,Y相互独立时,H(X|Y) = H(X),I(X,Y)最小,为0.
3.附录(信息量,信息熵与物理意义上的熵)
信息量:
1948年,香农在他著名的《通信的数学原理》论文中指出:“信息是用来消除随机不确定性的东西”,并提出了“信息熵”的概念来解决信息的度量问题。香农用信息熵的概念来描述信源的不确定度。
所谓某句话信息量大,是指用这些信息来进行预测会使得某事的预测变得更加精准,比如一本中文书比一个中文字的信息量大,因为通过这本书可以比较清晰地预测作者要表达的故事、情感和思想,而单个字却几乎无法预测。
日常中提到的信息量,可能和传递效率(有人说半天但只是表达了一个意思)、信息质量(比如可信度等)有关,和我们这儿谈到的信息量不同,我们文中谈到的信息量只和可能结果和各个结果之间的概率有关。
物理意义上的熵
表征某状态、某系统的不确定性的大小。系统越有序则信息熵越低。值越大,表示不确定性越大,系统的稳定性越好。玻尔兹曼给出的参数化和香农给出的参数化很相近,只是差常数因子。在封闭系统下,熵会达到最大值(即稳定状态,比如两种气体混合前总熵最低,混合好后总的熵最高);若使系统的熵减少(使系统更加有序化),必须有外部能量的干预。任何不可逆过程(大部分都是)宏观上会导致熵的增加;或者说微观上有极小概率会导致熵的减少,但到宏观上,就(几乎)不可能导致熵增加。
