特征提取算法

1、背景

特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。

特征提取（feature extraction）包括两部分：特征检测（feature detection）和特征描述（feature description）。假设我们使用object corners 作为特征，检测就是在一个区域或图像中寻找corners；描述就是给检测到的特征赋予定量属性（quantitative attributes），如 corner orientation和location。

特征是用来区分对象的，一般要independent于location, rotation, 和 scale，另外独立于illumination levels 和 changes caused by the viewpoint between the imaging sensor and the scene 也很重要。（平移不变性、旋转不变性、尺度不变性、光照不变性、视点不变性）
上面说的"independent"一词通常具有两种含义之一：invariant或covariant。特征描述子是不变的，即对于一系列的图像变换，其值保持不变；特征描述子是协变的，即对于一系列变换，应用任意一个变换会导致特征描述子发生相同的变换。通过协变量的规范化（normalize）可以转换为不变量，例如对于旋转是协变的，我们可以通过将特征描述子旋转至预定义的方向，这样旋转协变的特征描述子就转换为了旋转不变的也正描述子。

特征分为局部特征（local feature description）和全局特征（global）。如果一个特征适用于一个集合中的一个成员，则称这个特征是局部的；如果一个特征适用于整个集合，则称这个特征是全局的。“集合”和“成员”视具体任务而定。

特征提取算法通常会产生多个特征描述值，将这些数值特征打包称之为一个特征向量（feature vector），其元素都是描述子（descriptors）。如果采用n个descriptors，则特征向量是n维的，则包含所有特征向量的空间是一个n维特征空间（feature space）。

在特征提取之前应使用预处理操作对输入图像进行归一化（normalize），例如直方图均衡化或规定化（histogram equalization or specification），可以用于部分弥补光照变化的影响。

2、边界预处理

Moore boundary tracing algorithm

假设一幅二值图像，物体区域的像素值为1，背景区域像素为0，Moore边界跟踪算法流程如下：

1. 从左到右从上到下依次扫描图像，找到第一个像素值为1的点，作为起始点，记为$b_0$，将该点左边点记为$c_0$。
2. 令$b=b_0$，$c=c_0$，从$c$开始以顺时针方向扫描$b$的八邻域像素点，扫描过的序列依次记为$n_1,...,n_8$，假设序列中第一个像素值为1的点为$n_k$。
3. 令$b=n_k$，$c=n_{k-1}$，从$c$开始以顺时针方向扫描$b$的八邻域像素点，扫描过的序列依次记为$n_1,...,n_8$，假设序列中第一个像素值为1的点为$n_k$。
4. 重复第三步，直至$b=b_0$。算法停止时所有$b$点组成的序列是边界点的有序集合。

Chain Codes

链码通过指定长度和方向的直线段的连接序列来表示边界。

Freeman Chain Codes

定义四方向和八方向链码各个方向对应的数字。

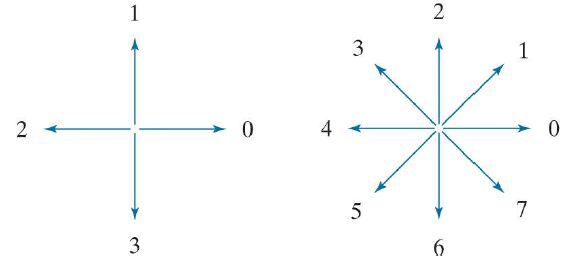
在实际使用中，不需要那么精细的链码（一是太长，二是些微扰动对边界形状影响很大），因此首先利用更大的网格间距对边界进行重采样，使得多个像素点落在一个网格内，根据原始像素点与网格结点的距离确定粗网格的边界点。然后以最左最上的边界点为起始点，顺时针方向按照以上的四方向或八方向数字定义对边界点进行数字编码。

• 链码可以相对于起点进行规范化（即对于任意起点，规范化的链码都相同）：将链码视为一个循环序列，并重新定义起点使得序列对应的数最小。
• 链码可以通过其一阶差分（first difference）对旋转进行规范化（即对边界进行任意方向旋转，规范化的链码都相同）。
  例如对于四方向链码10103322，我们先将其相对于起点规范化，得到链码01033221，其一阶差分的第一个数为最后一个数与起点相隔的方向数为3（因为最后一个数1要逆时针转动3次转到起点0），如图所示，一阶差分为3133030
  
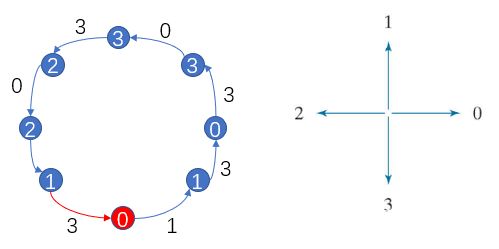
• 尺度规范化（Size normalization）可以通过改变重采样网格间距实现。

slope chain codes (SCCs)

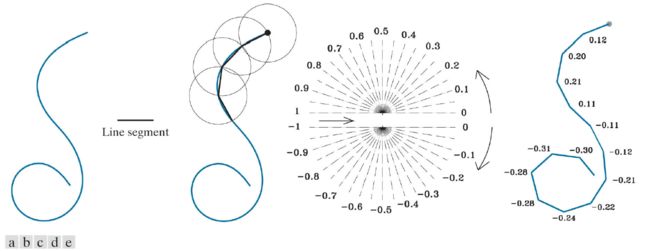
SCCs 通过用将某条固定长度线段的两个端点置于曲线上并遍历曲线得到，用一个斜率变化序列来表示，取值范围为(-1,1)，可以用来近似曲线。SCCs独立于旋转、平移，并且可以对尺度变化进行规范化。

minimum-perimeter polygon (MPP)

可以用边界的最小周长多边形（MPP）来近似表示边界。我们首先用一系列的cell 包围边界，称为 a cellular complex。则边界的MPP的顶点要么是 the cellular complex 内壁的凸顶点，要么是其内壁凹顶点对应的在外壁的镜像凹顶点。

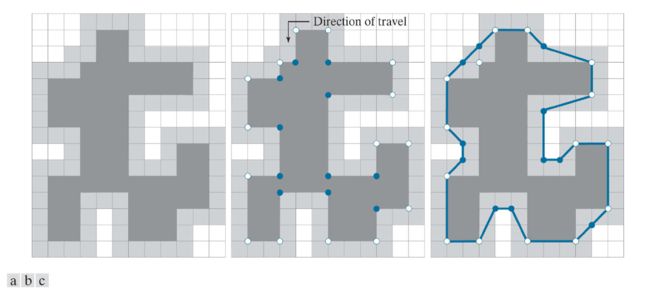
MPP算法通过遍历边界所有的顶点来判断该顶点是否为MPP的顶点。边界的顶点可以采用边界跟踪算法生成。

MPP可以用来近似表示边界，能大大减小数据量，此外对边界具有平滑效果（视网格大小而定）。

signatures

a signature 是用一个一维函数表示二维边界。

skeletons

边界(boundaries)和骨架(skeletons)都可以用来描述区域形状。骨架可以通过两种方法获得：基于形态学的腐蚀变薄处理；基于距离变换获得区域中轴的方法。

3、Region Feature Descriptors

3.1 区域描述子和特征向量

• The major and minor axes of a region

• The bounding box of a region

• The area of a region $A$：the number of pixels in the region

• The perimeter of a region $p$：the length of its boundary

• compactness(dimensionless measure)：$compactness=\frac{p^2}{A}$

• circularity/roundness(dimensionless measure)：$circularity=\frac{4\pi A}{p^2}$
  （$compactness$和$circularity$ are independent of size, orientation, and translation.）

• The effective diameter：$d_e=2\sqrt{\frac{A}{\pi }}$ (independent of orientation and translation)

• The eccentricity of a region：等于与该区域具有相同二阶中心矩的椭圆的离心率
  （ $椭圆离心率=\frac{c}{a}=\frac{\sqrt{a^2-b^2}}{a}=\sqrt{1-(\frac{b}{a}{)}^2}$ (a>=b) 即椭圆中心到焦点的距离与椭圆中心到主轴端点距离的比值）
  （给定一个区域，我们令椭圆的主轴和副轴分别与区域的轴对齐，获得该区域的近似椭圆。定义协方差矩阵$C$：$C=\frac{1}{K-1}{\sum }_{k=1}^K(z_k-\overline{z})(z_k-\overline{z}{)}^T$。其中$z_k$是一个二维向量，其元素为区域中像素点的坐标；$K$为像素点个数；$\overline{z}$是均值向量。主轴和副轴长度的一半$a$和$b$分别为协方差矩阵的最大值和最小值，主轴和副轴的方向分别为特征值对应的特征向量方向。 另外有结论：圆的离心率为0；直线的离心率为1。离心率的范围为[0,1]。）

通常一个描述子无法区分个体。我们将多个描述子组合成一个特征向量，所有这样的特征向量构成特征空间。 在特征空间中，我们更易看出个体间的相似性和差异性。

3.2 Topological Descriptors

Topology：研究图形不受任何变形影响（如拉伸、旋转）的特性，假设不存在撕裂（no tearing）和折叠的情况。(例如：区域空洞的个数)

• The Euler number $E$ of a region：$E=C-H$。（the number of holes $H$, and connected components $C$）
• Euler formular：$V-Q+F=C-H$。（对于由线段组成的区域（如多边形网络），denoting the number of vertices by $V$, the number of edges by $Q$, and the number of faces by $F$，有Euler formular。）

3.3 Texture

一般描述区域的纹理可以通过：smoothness, coarseness, and regularity …

• statistical approaches for describing the texture of a region：smooth. coarse, grainy …
• spectral approaches：detect global periodicity

statistical approaches： 利用灰度直方图的统计矩

设$z$是表示灰度的随机变量，$p(z_i),i=0,1,...,L-1$ 为对应的归一化直方图，则$z$的$n$阶矩为：
$${\mu }_n(z)=\sum _{i=0}^{L-1}(z_i-m{)}^{n}p(z_i)$$

其中，$m={\sum }_{i=0}^{L-1}{z}_{i}p(z_i)$。
可以发现，

• ${\mu }_0=1,{\mu }_1=0$。
• 二阶矩${\mu }_2={\sigma }^2(z)$是比较重要的纹理描述子。（It’s a measure of intensity contrast that can be used to establish descriptors of relative intensity smoothness：$R(z)=1-\frac{1}{1+\frac{{\sigma }^2(z)}{(L-1{)}^2}}$。 常亮度区域$R=0$。方差越大的区域$R$越接近1。）
• the third moment ${\mu }_3(z)$ is a measure of the skewness of the histogram.
• the fourth moment ${\mu }_4(z)$ is a measure of its relative flatness.
• uniformity：$U(z)={\sum }_{i=0}^{L-1}{p}^2(z_i)$。（常数区域，$U$最大）
• average entropy：$e(z)=-{\sum }_{i=0}^{L-1}p(z_i){\log }_{2}p(z_i)$。（常数区域，$e=0$）

总结：

• mean 反映整体亮度水平，但不反映纹理，一般不作为纹理描述子
• standard deviation 和 $R$ 一样，反映纹理的光滑性，值越小表明越光滑（常数区域值为0）
• third moment 反映了直方图的对称性，小于0表示直方图偏左，大于0表示偏右，即表示整体图像亮度偏暗或偏亮
• uniformity 均匀性。粗纹理对应于低值，值越大表明图像越光滑
• entropy 不确定性。随着uniformity的减小而增大，值越小，表明亮度变化越小，图像越光滑

statistical approaches： 利用灰度灰度共生矩阵

仅利用直方图计算的纹理描述子不包含像素的空间位置信息。为了引入空间位置信息，采取graylevel co-occurrence matrix。
定义灰度共生矩阵： 假设$Q$是位置算子，co-occurrence matrix $G$ is a matrix whose element $g_{ij}$ is the number of times that pixel pairs with intensities $z_i$ and $z_j$ occur in image $f$ in the position specified by $Q$。（即灰度共生矩阵$G$的元素$g_{ij}$表示像素$z_i$和$z_j$在满足$Q$指定的位置关系下在图像$f$中出现的次数。）
The quantity $p_{ij}=\frac{g_{ij}}{n}$ is an estimate of the probability that a pair of points satisfying $Q$ will have values $(z_i,z_j)$。

基于共生矩阵的纹理描述子：

• maximum probability： $\underset{i,j}{\max }(p_{ij})$

spectral approaches： 基于傅里叶频谱

傅里叶频谱的特征可以用作纹理描述（周期性纹理）。

LBP特征

LBP（Local Binary Pattern, 局部二值模式）是一种用来描述图像局部纹理特征的算子。
（1）首先将图像划分为16×16的小区域（cell）；
（2）对每个cell中的每个像素，将相邻的8个像素的灰度值与之比较，若大于该灰度值，则标记为1，否则标记为0。33邻域内的8个点经比较可产生8位二进制数，即为该像素点的LBP值。
（3）将二进制LBP值转换为十进制，计算每个cell的LBP直方图，即统计每个LBP值出现的频率，并对直方图进行归一化。
（4）将1616个cell的直方图进行连接得到一个特征向量，即整幅图的LBP纹理特征向量。
然后便可利用SVM或者其他机器学习算法进行分类了。

应用：纹理特征提取，提取的特征是图像的局部纹理特征

3.4 Moment Invariants

The 2-D moment of order $(p+q)$ of an $M\times N$ digital image $f(x,y)$：
$$m_{pq}=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}{x}^p{y}^{q}f(x,y)$$

The corresponding central moment of order $(p+q)$：
$${\mu }_{pq}=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}(x-\overline{x}{)}^p(y-\overline{y}{)}^{q}f(x,y)$$

其中，$\overline{x}=\frac{m_{10}}{m_{00}}$，$\overline{y}=\frac{m_{01}}{m_{00}}$。
The normalized central moment of order $(p+q)$：
$${\eta }_{pq}=\frac{{\mu }_{pq}}{{\mu }_{00}^{\gamma }}$$

其中，$\gamma =\frac{p+q}{2}+1$ for $p+q=2,3,...$
一组共7个2-D moment invariants can be derived from the second and third normalized central moments：${\varphi }_1,{\varphi }_2,...,{\varphi }_7$。这组矩对于平移、尺度变化、镜像、旋转都是不变的（invariant）。

4、Principal Components as Feature Descriptors

假设有$n$幅图像，对于任一位置，这$n$幅图像对应位置的像素组成一个$n$维列向量：
$$x=\left(\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right)$$

我们将$x$视为一个随机向量，并定义均值向量和协方差矩阵：
$$m_x=E\{x\}$$

$$C_x=E\{(x-m_x)(x-m_x{)}^T\}$$

由于$x$是一个$n$维列向量，则$C_x$是一个$n\times n$矩阵。$C_{ii}$表示向量$x$的第$i$个分量的方差，$C_{ij}$表示向量$x$中的$x_i$与$x_j$的协方差。如果$x_i$和$x_j$不相关，则$C_{ij}=0$。
$C_x$是一个实对称矩阵，总可以找到$n$个正交的特征向量。令矩阵$A$的每一行为$C_x$的特征向量，且对应的特征值按从大到小排序（即$A$的第一行是最大特征值对应的特征向量）。

Hotelling Transform (principal components transform)

作变换：
$$y=A(x-m_x)$$

有性质：$m_y=0$，$C_y=AC{A}^T$。$C_y$是一个对角矩阵，对角线上的元素为其特征值按从大到小排序。因此向量$y$的各个分量互不相关。$C_x$和$C_y$具有相同的特征值。

通过$y$可以重建$x$： ($A$为正交矩阵，$A^T=A^{-1}$)
$$x=A^{T}y+m_x$$

假设$A_k$是由$k$个最大特征值对应的特征向量组成的，$A_k$的维度为$k\times n$，作变换：
$$y_k=A_k(x-m_x)$$

(可以发现 $x_{n\times 1}$ --> $y_{k\times 1}$ 实现了降维。)
利用$y_k$我们获得$x$的近似：
$$\hat{x}=A_k^{T}y+m_x$$

$x$与$\hat{x}$的均方误差为：$e_{ms}={\sum }_{j=k+1}^n{\lambda }_j$。

使用主成分对尺寸、平移、旋转变化进行归一化

假设有一个物体，我们记物体像素点的坐标为$x=(x_1,x_2{)}^T$，物体区域的所有像素点构成数据总体，求其均值向量和协方差矩阵，然后对这个物体区域实行主成分变换。式子$y=A(x-x_m)$做了两件事：（1）$x-x_m$将变换后的原点确定为物体的质心；（2）变换后的y坐标向量是x的旋转，即将坐标轴与两个特征向量的方向对齐。

1、SIFT

尺度不变特征转换（Scale-invariant feature transform 或SIFT）用于检测和描述图像的局部性特征，它在空间尺度中寻找极值点，并提取出位置、尺度、旋转不变量，对于光线、噪声以及微小视角改变的容忍度较高。

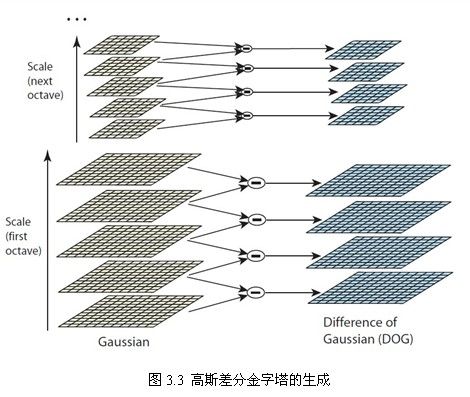
（1）构建高斯差分金字塔

高斯滤波是实现尺度变换的唯一变换核。

• $I(x,y)$表示原图像。
• $G(x,y,\sigma )$表示高斯滤波器，其中$G(x,y,\sigma )=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$。
• $L(x,y,\sigma )=G(x,y,\sigma )\otimes I(x,y)$。一系列的${\sigma }_i$可以生成一系列的$L(x,y,{\sigma }_i)$图像。这一系列图像称为原图像的一个尺度空间表示。
• $DoG$表示高斯差分（Difference of Gaussians）。$D(x,y,\sigma )=(G(x,y,k\sigma )-G(x,y,\sigma ))\otimes I(x,y)=L(x,y,k\sigma )-L(x,y,\sigma )$。

使用高斯差分函数的原因：尺度归一化的高斯拉普拉斯函数${\sigma }^2{\nabla }^{2}G$的极大值和极小值相比其他特征提取函数，如梯度、Hessian 或Harris角特征，能够产生最稳定的图像特征。而高斯差分函数近似于尺度归一化的高斯拉普拉斯函数。

在实际计算中，使用高斯金字塔每组中相邻上下两层图像相减，得到高斯差分图像。然后进行极值检测。

（2）特征点的搜索

尺度空间极值点检测（关键点的初步探查）

为了在高斯差分金字塔中寻找尺度空间的极值点，每个采样点要和它所有的相邻点进行比较，包括图像域和尺度域。即对于任意一个检测点要和它同尺度的8个相邻点以及上下相邻尺度的9*2个点共26个点比较。

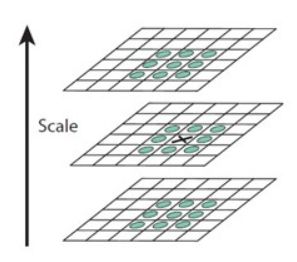
搜索过程从每组的第二层开始，以第二层为当前层，对第二层的DoG图像中的每个点取一个3×3的立方体，立方体上下层为第一层与第三层。这样搜索得到的极值点既有位置坐标又有空间尺度坐标。当S=3时，每组要搜索3层。

这样产生的极值点并不全是稳定的特征点，因为某些极值点响应较弱，而且DoG算子会产生较强的边缘响应。

子像元插值

上面的尺度空间极值点的搜索是在离散空间中进行的，检测到的极值点并不是真正意义上的极值点。需要利用已知的离散空间点插值到连续空间极值点，即子像元插值。

通过多次迭代得到最终候选点的精确位置与尺度，将其代入公式求得$D(x)$，并求其绝对值。如果其绝对值低于阈值的将被删除。

删除边缘效应

选取$\gamma =10$，即主曲率比值大于10的特征点将被删除。

参考资料：
[1] SIFT定位算法关键步骤的说明

2、Harris角点检测算子

Harris角点检测算子具有旋转不变性和尺度不变性，且对亮度和对比度变化不敏感。

若某个窗口内的图像存在角点，则在各个方向上移动这个特征的小窗口，窗口内区域的灰度会发生较大的变化。因此对于图像$I(x,y)$，定义点$(x,y)$平移$(\Delta x,\Delta y)$后的自相似性，即自相关函数：
$$c(x,y;\Delta x,\Delta y)=\sum _{w(u,v)\in W(x,y)}w(u,v)(I(u,v)-I(u+\Delta x,v+\Delta y){)}^2$$

该函数可近似为二项函数：
$$c(x,y;\Delta x,\Delta y)\approx A\Delta x^2+2C\Delta x\Delta y+B\Delta y^2=\left[\Delta x,\Delta y\right]M(x,y)\left[\begin{array}{c}\Delta x\\ \Delta y\end{array}\right]$$

其中，
$$A=\sum _w{I}_x^2,B=\sum _w{I}_y^2,C=\sum _w{I}_x{I}_y,M(x,y)=\left[\begin{array}{cc}A& C\\ C& B\end{array}\right]$$

当$M$的两个特征值都大且近似相等时，存在角点。我们可以通过计算一个角点响应值$R$来判断角点。
$$R=detM-\alpha (traceM{)}^2$$

其中, $\alpha$的取值范围为$0.04\sim 0.06$，
$$detM={\lambda }_1{\lambda }_2=AC-B^2$$

$$traceM={\lambda }_1+{\lambda }_2=A+C$$

算法流程如下：

• （1）计算图像$I(x,y)$在$X$和$Y$两个方向的梯度$I_x$、$I_y$。
• （2）计算图像两个方向上梯度的乘积$I_x^2$、$I_y^2$和$I_{xy}=I_x{I}_y$。
• （3）进行高斯加权，生成矩阵$M$的元素$A$、$B$和$C$。
  $$A=g(I_x^2)=I_x^2\otimes w,C=g(I_y^2)=I_y^2\otimes w,B=g(I_{xy})=I_{xy}\otimes w$$
• （4）计算每个像素的Harris响应值$R$，并对小于某一阈值$t$的$R$置为0。
• （5）在3×3或5×5的邻域内进行非极大值抑制，局部最大值即为图像中的角点。

3、HOG

HOG(Histogram of Oriented Gradient，方向梯度直方图)用于描述图像局部纹理的特征。HOG特征通过激素那和统计图像局部区域的方向梯度直方图来构成特征。
思想：在一幅图像中，局部目标的表象和形状能够被梯度或边缘的方向密度分布很好地描述。其本质为：梯度的统计信息，而梯度主要存在于边缘的地方。

算法步骤：
（1）灰度化和Gamma校正：能够有效降低阴影和光照变化的影响。
（2）计算梯度的幅值和方向：
（3）构建方向的直方图：将图像分为若干个cell。假设每个cell为6*6个像素，假设采用9个bin的方向直方图来统计梯度信息（即将360度分为9个方向块，第一个bin是0~40°，第2个bin是40-80° ）。假设某个像素梯度大小为2，方向为30°，则梯度方向直方图的第一个bin计数加2（即梯度大小用来作权值，用双线性内插法将幅值累加到直方图中?）。这样每个cell都能计算出一个梯度方向直方图，即对应的特征向量（上述为9维的特征向量）。
（4）把小cell组合成更大的block，block内归一化梯度直方图：将小cell组合成大的、空间上连通的blocks。一个block内所有cell的特征向量串联起来便得到该block的HOG特征（归一化去除光照和阴影的影响）。（注意，这些blocks是有重叠的，即每个cell的特征会以不同的结果多次出现在最后的特征向量中，我们将归一化后的block描述符称为HOG描述符。）
（5）收集所有blocks的特征，并将它们结合成最终的特征向量供分类使用。

应用：HOG+SVM进行行人检测

参考资料：
[1]Harris角点
[2]图像特征提取三大法宝：HOG特征，LBP特征，Haar特征