（2）聚类算法之K-means算法

1.引言

        K-means算法是一种聚类算法，所谓聚类，即根据相似性原则，将具有较高相似度的数据对象划分至同一类簇，将具有较高相异度的数据对象划分至不同类簇。聚类与分类最大的区别在于，聚类过程为无监督过程，即待处理数据对象没有任何先验知识，而分类过程为有监督过程，即存在有先验知识的训练数据集。
        K-means算法中的$K$代表类簇个数，means代表类簇内数据对象的均值 （当有部分异常点时，求均值是不合理的，即一个特大都值，或者极小的值，会影响均值的数值），因此，K-means算法又称为k-均值算法，k-means算法是一种基于划分的聚类算法，以距离作为数据对象间相似性度量的标准，即数据对象间的距离越小，则它们的相似性越高，则它们越有可能在同一个类簇。数据对象间距离的计算有很多种，k-means算法通常采用欧氏距离来计算数据对象间的距离。

2.K-means算法原理

        K-means算法以距离作为数据对象间相似性度量的标准，通常采用欧氏距离来计算数据对象间的距离。下面给出欧式距离的计算公式 ($x$代表据具有$m$个属性的行向量)：
$$dist(x_i,x_j)=\sqrt{(x_i-x_j)(x_i-x_j{)}^T}\text{\hspace{1em}(1)}$$

        K-means算法聚类过程中，每次迭代，对应的类簇中心需要重新计算（更新）：对应类簇中所有数据对象的均值，即为更新后该类簇的类簇中心。定义第$K$个类簇的类簇中心为$Cente{r}_k$，则类簇中心更新方式如下：

$$Cente{r}_k=\frac{1}{|C_k|}\sum _{x_i\in C_k}{x}_i\text{\hspace{1em}(2)}$$
其中，$C_k$表示第$k$个类簇，$|C_k|$表示第$k$个类簇中数据对象的个数，这里的求和是指类簇$C_k$中所有元素在每列属性上的和，因此$Cente{r}_k$也是一个含有$m$个属性的行向量。

K-means算法需要不断地迭代来重新划分类簇，并更新类簇中心，那么迭代终止的条件是什么呢？ 一般情况，有两种方法来终止迭代：(1)一种方法是设定迭代次数$T$，当到达第$T$次迭代，则终止迭代，此时所得类簇即为最终聚类结果；(2)另一种方法是采用误差平方和准则函数，函数模型如下：
$$J=\sum _{k=1}^K\sum _{x_i\in C_k}dist(x_i,Cente{r}_k)\text{\hspace{1em}(3)}$$
此公式表示，所有类数据与其中心的距离和。其中，$K$表示类簇个数。当两次迭代J的差值小于某一阈值时，即$\Delta J<\delta$时，则终止迭代，此时所得类簇即为最终聚类结果。即下次类中心都移动距离不大聚类完毕

        $K-means$算法思想可描述为：

1. 初始化$K$个簇集中心，然后计算各个数据对象到簇集中心的距离，把数据对象划分至距离其最近的聚类中心所在簇集中，并求距离和$J1$，跳转到2
2. 根据所得簇集，得到新的簇集中心；同时计算新的距离和$J2$，跳转到3
3. 计算$\Delta J$，判断$\Delta J$是否小于阈值或者循环次数是否大于$T$，如果小于阈值或者循环次数大于$T$，跳出循环，结束聚类。否则跳转到4
4. 根据所得簇集，得到新的簇集中心；同时计算新的距离和$J1$

算法详细流程描述如下：

3.K-means算法实现

3.1 numpy实现K-means算法

• 在迭代的过程中，首先判断容差，等容差小于某个值时就停止迭代，但是如果长时间不收敛，就根据迭代次数停止迭代。这样算法就拥有更好健壮性

import numpy as np
import random
import time
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
# 计算两个矩阵的距离矩阵
def compute_distances_no_loops(A, B):
    return cdist(A,B,metric='euclidean')
    
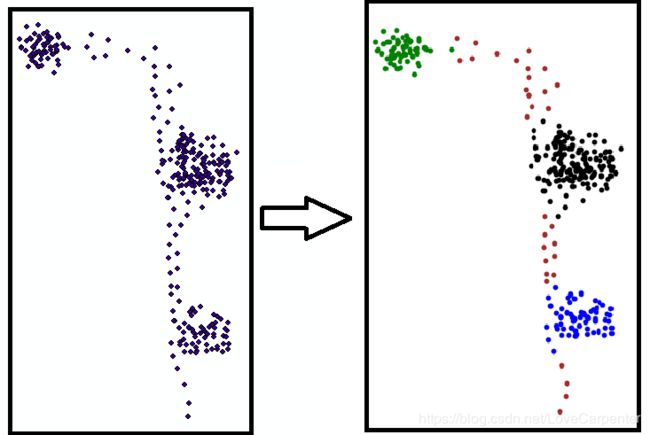
# 显示簇集，如果簇集类别大于6类，需要增加colorMark的内容
def plotFeature(data, labels_):
    clusterNum=len(set(labels_))
    fig = plt.figure()
    scatterColors = ['black', 'blue', 'green', 'yellow', 'red', 'purple', 'orange', 'brown','#BC8F8F','#8B4513','#FFF5EE']
    ax = fig.add_subplot(111)
    for i in range(-1,clusterNum):
        colorSytle = scatterColors[i % len(scatterColors)]
        subCluster = data[np.where(labels_==i)]
        ax.scatter(subCluster[:,0], subCluster[:,1], c=colorSytle, s=20)
    plt.show()

# 聚类算法的实现
# 需要聚类的数据data
# K 聚类的个数
# tol 聚类的容差，即ΔJ
# 聚类迭代都最大次数N
def K_means(data,K,tol,N):
    #一共有多少条数据
    n = np.shape(data)[0]
    # 从n条数据中随机选择K条，作为初始中心向量
    # centerId是初始中心向量的索引坐标
    centerId = random.sample(range(0, n), K)
    # 获得初始中心向量,k个
    centerPoints = data[centerId]
    # 计算data到centerPoints的距离矩阵
    # dist[i][:],是i个点到三个中心点的距离
    dist = compute_distances_no_loops(data, centerPoints)
    # axis=1寻找每一行中最小值都索引
    # squeeze()是将label压缩成一个列表
    labels = np.argmin(dist, axis=1).squeeze()
    # 初始化old J
    oldVar = -0.0001
    # data - centerPoint[labels]，获得每个向量与中心向量之差
    # np.sqrt(np.sum(np.power(data - centerPoint[labels], 2)，获得每个向量与中心向量距离
    # 计算new J
    newVar = np.sum(np.sqrt(np.sum(np.power(data - centerPoints[labels], 2), axis=1)))
    # 迭代次数
    count=0
    # 当ΔJ大于容差且循环次数小于迭代次数，一直迭代。负责结束聚类
    # abs(newVar - oldVar) >= tol:
    while count<N and abs(newVar - oldVar) > tol:
        oldVar = newVar
        for i in range(K):
            # 重新计算每一个类别都中心向量
            centerPoints[i] = np.mean(data[np.where(labels == i)], 0)
        # 重新计算距离矩阵
        dist = compute_distances_no_loops(data, centerPoints)
        # 重新分类
        labels = np.argmin(dist, axis=1).squeeze()
        # 重新计算new J
        newVar = np.sum(np.sqrt(np.sum(np.power(data - centerPoints[labels], 2), axis=1)))
        # 迭代次数加1
        count+=1
    # 返回类别标识，中心坐标
    return labels,centerPoints
starttime = time.clock()
data = np.loadtxt("cluster.csv", delimiter=",")
labels,_=K_means(data,3,0.01,100)
endtime = time.clock()
print(endtime - starttime)
plotFeature(data, labels)

3.2 使用scikit-learn实现K-means算法

import numpy as np
from sklearn.cluster import KMeans
# 加载数据
data = np.loadtxt("cluster.csv", delimiter=",")
# 构造一个聚类数为3的聚类器
estimator = KMeans(n_clusters=3,max_iter=100,tol=0.001)
# 实现聚类结果
estimator.fit(data)
# 获取聚类标签
label_pred = estimator.labels_
# 获取聚类中心
centroids = estimator.cluster_centers_
# 获取聚类准则的总和
inertia = estimator.inertia_

4 .K-means优缺点

• 优点：
    算法简单易实现；
• 缺点：
    需要用户事先指定类簇个数K；
    对异常点敏感，一个特大都值，或者极小的值，会影响均值的数值
    聚类结果对初始类簇中心的选取较为敏感；
    容易陷入局部最优；
    只能发现球型类簇；

5. 代码及数据下载地址

• GitHub的数据及代码下载地址为：GitHub的数据及代码下载链接（如果从GitHub下载代码，麻烦给小Demo一个Star，您的支持是我最大的动力）