3D渲染管线中的坐标变换

3D物体被渲染到屏幕之前，会经历以下的坐标变换：

• 局部坐标 Local Coordinates
• 世界坐标 World Coordinates
• 相机坐标 Camera Coordinates
• 透视坐标 Perspective Coordinates
• 屏幕坐标 Screen Coordinates

在不考虑光照计算、着色处理和纹理映射，只考虑几何变换的情况下，3D渲染管线中的坐标变换流程如下：

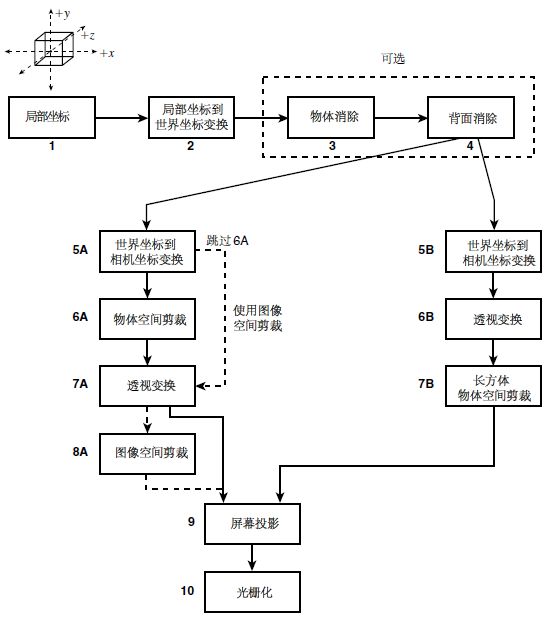
该变换流程，将3D模型的局部坐标，变换到屏幕坐标。
本文先不考虑物体消除、背面消除和物体空间的剪裁。

---

一、局部坐标

局部坐标也叫模型坐标，使用局部坐标，可以将模型平移到世界坐标中的实际位置。
可以将物体的中心当做局部坐标系的原点，如下图所示的立方体：

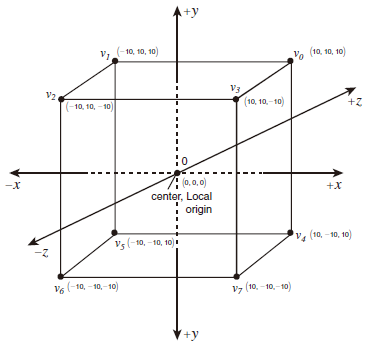
立方体边长为10个单位，中心坐标为(0,0,0)，各顶点在局部坐标系中的坐标如下：

Vertex 0: (10,10,10)		Vertex 1: (-10,10,10)
Vertex 2: (-10,10,-10)		Vertex 3: (10,10,-10)
Vertex 4: (10,-10,10)		Vertex 5: (-10,-10,10)
Vertex 6: (-10,-10,-10)		Vertex 7: (10,-10,-10)

也可以将其他位置作为局部坐标系的原点，例如下图所示的机器人手臂：

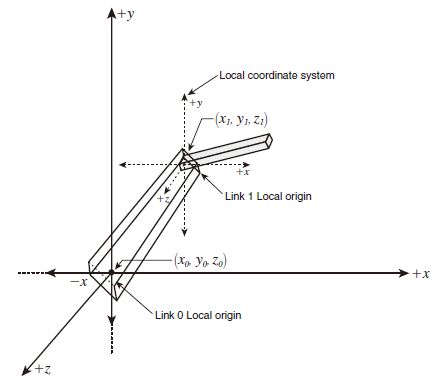
可以将手臂的一端作为局部坐标系的原点，从而实现旋转摆动手臂的动作。

我们可以将旋转和缩放放到局部坐标变换中完成。

---

二、世界坐标

将局部坐标变换到世界坐标，只需将物体平移到世界坐标的某个位置即可。
假设游戏的世界大小为1000x1000x1000，且要将模型平移到世界空间中的位置$(x_w,y_w,z_w)$：

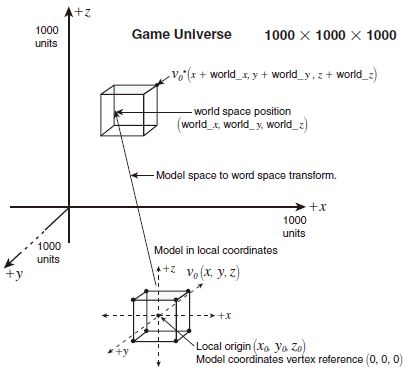
则有平移矩阵形式如下：
$${\mathbf{T}}_{\mathbf{m}\mathbf{w}}=\left[\begin{array}{cccc}1& 0& 0& 0\\ & & & \\ 0& 1& 0& 0\\ & & & \\ 0& 0& 1& 0\\ & & & \\ x_w& y_w& z_w& 1\\ & & & \end{array}\right]$$

将向量和矩阵相乘，可以实现模型坐标到世界坐标的平移，矩阵运算如下：

$${\mathbf{V}}_{\mathbf{m}}{\mathbf{T}}_{\mathbf{m}\mathbf{w}}={\left[\begin{array}{c}{x}_m\\ \\ y_m\\ \\ z_m\\ \\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccc}1& 0& 0& 0\\ & & & \\ 0& 1& 0& 0\\ & & & \\ 0& 0& 1& 0\\ & & & \\ x_w& y_w& z_w& 1\\ & & & \end{array}\right]={\left[\begin{array}{c}{x}_m+x_w\\ \\ y_m+y_w\\ \\ z_m+z_w\\ \\ 1\end{array}\right]}^{\mathrm{T}}$$

---

三、相机坐标

相机的参数：

• 相机在世界坐标中的位置
• 相机的方向
• 视野 FOV
• 远剪裁面和近剪裁面 —— 只有位于远近剪裁面之间的物体才可见，其他物体都不可见
• 视平面/投影面 —— 3D图像会投影到这个平面
  

将世界坐标变换为相机坐标：
对世界中的物体进行变换，使其位置是相对于相机的。因此，要人为地将物体从世界坐标系变换到相机坐标系，使得相机位于世界坐标系的原点，并指向+Z轴方向。

在图形学中，物体的运动是相对的，要移动相机，使得相机位于世界坐标系的原点，并指向+Z轴方向，只需相应移动所有的物体。这种变换分两步完成：先平移，后旋转。

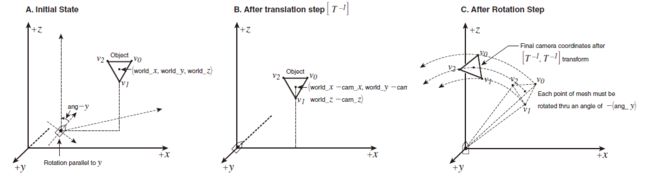
A：平移前，物体的位置为$P_{obj}=(worl{d}_x,worl{d}_y,worl{d}_z)$，相机的位置为$P_{cam}=(ca{m}_x,ca{m}_y,ca{m}_z)$
B：平移后，物体的位置为$P_{obj}-P_{cam}$
C：旋转后，物体的世界坐标变换到了相机坐标。

平移矩阵最下面一行是相机位置求反：
$${{\mathbf{T}}_{\mathbf{c}\mathbf{a}\mathbf{m}}}^{-1}=\left[\begin{array}{cccc}1& 0& 0& 0\\ & & & \\ 0& 1& 0& 0\\ & & & \\ 0& 0& 1& 0\\ & & & \\ -ca{m}_x& -ca{m}_y& -ca{m}_z& 1\\ & & & \end{array}\right]$$

绕三个轴旋转的旋转矩阵，旋转角度也要取反：
$${{\mathbf{R}}_{\mathbf{c}\mathbf{a}\mathbf{m}\mathbf{x}}}^{-1}=\left[\begin{array}{cccc}1& 0& 0& 0\\ & & & \\ 0& \cos (-{\theta }_x)& \sin (-{\theta }_x)& 0\\ & & & \\ 0& -\sin (-{\theta }_x)& \cos (-{\theta }_x)& 0\\ & & & \\ 0& 0& 0& 1\\ & & & \end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ & & & \\ 0& \cos ({\theta }_x)& -\sin ({\theta }_x)& 0\\ & & & \\ 0& \sin ({\theta }_x)& \cos ({\theta }_x)& 0\\ & & & \\ 0& 0& 0& 1\\ & & & \end{array}\right]$$

$${{\mathbf{R}}_{\mathbf{c}\mathbf{a}\mathbf{m}\mathbf{y}}}^{-1}=\left[\begin{array}{cccc}\cos (-{\theta }_y)& 0& -\sin (-{\theta }_y)& 0\\ & & & \\ 0& 1& 0& 0\\ & & & \\ \sin (-{\theta }_y)& 0& \cos (-{\theta }_y)& 0\\ & & & \\ 0& 0& 0& 1\\ & & & \end{array}\right]=\left[\begin{array}{cccc}\cos ({\theta }_y)& 0& \sin ({\theta }_y)& 0\\ & & & \\ 0& 1& 0& 0\\ & & & \\ -\sin ({\theta }_y)& 0& \cos ({\theta }_y)& 0\\ & & & \\ 0& 0& 0& 1\\ & & & \end{array}\right]$$

$${{\mathbf{R}}_{\mathbf{c}\mathbf{a}\mathbf{m}\mathbf{z}}}^{-1}=\left[\begin{array}{cccc}\cos (-{\theta }_z)& \sin (-{\theta }_z)& 0& 0\\ & & & \\ -\sin (-{\theta }_z)& \cos (-{\theta }_z)& 0& 0\\ & & & \\ 0& 0& 1& 0\\ & & & \\ 0& 0& 0& 1\\ & & & \end{array}\right]=\left[\begin{array}{cccc}\cos ({\theta }_z)& -\sin ({\theta }_z)& 0& 0\\ & & & \\ \sin ({\theta }_z)& \cos ({\theta }_z)& 0& 0\\ & & & \\ 0& 0& 1& 0\\ & & & \\ 0& 0& 0& 1\\ & & & \end{array}\right]$$
上述三个旋转矩阵的推导可参考：3D旋转矩阵的推导
综合上述四个矩阵，世界坐标到相机坐标的变换矩阵为：
$${\mathbf{T}}_{\mathbf{w}\mathbf{c}}={{\mathbf{T}}_{\mathbf{c}\mathbf{a}\mathbf{m}}}^{-1}{{\mathbf{R}}_{\mathbf{c}\mathbf{a}\mathbf{m}\mathbf{x}}}^{-1}{{\mathbf{R}}_{\mathbf{c}\mathbf{a}\mathbf{m}\mathbf{y}}}^{-1}{{\mathbf{R}}_{\mathbf{c}\mathbf{a}\mathbf{m}\mathbf{z}}}^{-1}$$

---

四、透视坐标

透视变换（投影变换）：从相机坐标到透视坐标的变换。本质上就是做一个透视除法，实现近大远小的效果。
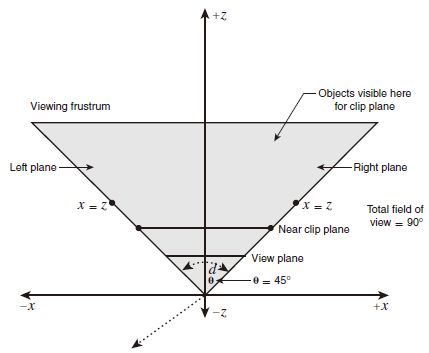
视距$d$：视平面和投影点（视点）之间的距离。
视平面（viewplane）：

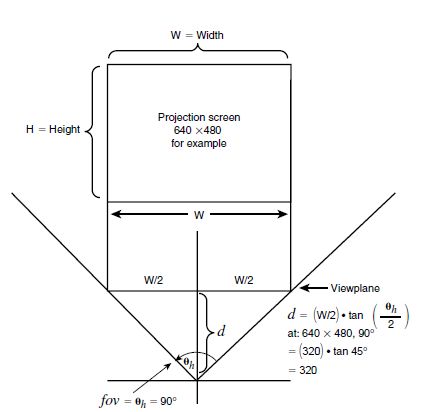
视距计算公式：
$$d=W/2\times \tan ({\theta }_h/2)$$

透视变换：将所有物体投影到视平面上。给定视距$d$，可以计算出物体上的点和视点的连线与视平面的交点：

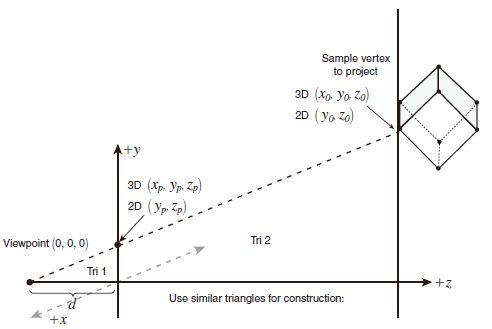
根据三角形相似，可得透视坐标：
$$\{\begin{array}{l}{X}_{per}=d{x}_0/z_0\\ Y_{per}=d{y}_0/z_0\end{array}$$

---

五、屏幕坐标

屏幕变换

视口（viewport） = 屏幕 （screen）= 光栅化窗口

屏幕变换：将视平面坐标转换到屏幕坐标。

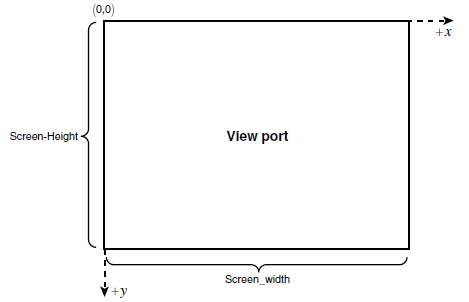
屏幕的原点是(0,0)，位于左上角，屏幕宽高分别为$W_s$和$H_s$，屏幕大小为$W_s\times H_s$，宽高比$ar=W_s/H_s$，且y轴被反转，如下图所示：

1.视野为90度且视距为1的情况
在这种情况下，透视空间中，视平面的坐标在每个轴上被归一化为-1到1。
$X_{per}$（从-1到1） 转换到 $X_{screen}$ （从0到$W_s-1$)
$Y_{per}$（从-1到1） 转换到 $Y_{screen}$ （从0到$H_s-1$)

$$\{\begin{array}{l}{X}_{screen}=(X_{per}+1)/2\times (W_s-1)\\ Y_{screen}=(Y-1)-(Y_{per}+1)/2\times (H_s-1)\end{array}$$

令$\alpha =(W_s-1)/2$，$\beta =(H_s-1)/2$，则有
$$\{\begin{array}{l}{X}_{screen}=\alpha +\alpha X_{per}\\ Y_{screen}=\beta -\beta Y_{per}\end{array}$$
其中，$(\alpha ,\beta )$是屏幕中心坐标。

2.一般情况：任意视野和任意视距的情况
在任意视野和任意视距的情况下，我们使用公式$d=W/2\times \tan ({\theta }_h/2)$来计算视距，因为没有被归一化，同样令$\alpha =(W_s-1)/2$，$\beta =(H_s-1)/2$，则有
$$\{\begin{array}{l}{X}_{screen}=\alpha +X_{per}\\ Y_{screen}=\beta -Y_{per}\end{array}$$

---

参考资料：

1. 《3D游戏编程大师技巧》 p328-362