吴恩达机器学习课后作业Python实现:第一周:线性回归
单变量线性回归
题目描述:在本部分的练习中,您将使用一个变量实现线性回归,以预测食品卡车的利润。假设你是一家餐馆的首席执行官,正在考虑不同的城市开设一个新的分店。该连锁店已经在各个城市拥有卡车,而且你有来自城市的利润和人口数据。
您希望使用这些数据来帮助您选择将哪个城市扩展到下一个城市。
数据集链接(数据在第一个文件内,需要自己查找):ex1data.txt
下面为读入数据和数据的展示
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'ex1data.txt'
# names添加列名,header用指定的行来作为标题,若原来无标题则设为none
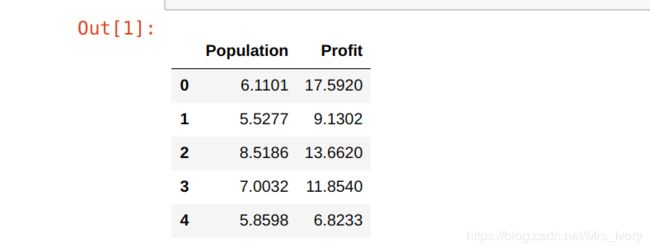
data = pd.read_csv(path,names=['Population','Profit'])
data.head()
在开始任何任务之前,通过可视化来理解数据通常是有用的。
对于这个数据集,您可以使用散点图来可视化数据,因为它只有两个属性(利润和人口)。
(你在现实生活中遇到的许多其他问题都是多维度的,不能在二维图上画出来。)
data.plot(kind='scatter', x='Population', y='Profit', figsize=(8,5))
plt.show()
# 在训练集中插入一列1,方便计算,只需要插入一次,如果多次允许时,该句需要删除
data.insert(0, 'Ones', 1)
# 设置训练集X,和目标变量y的值
cols = data.shape[1] # 获取列数
X = data.iloc[:,0:cols-1] # 输入向量X为前cols-1列
y = data.iloc[:,cols-1:cols] # 目标变量y为最后一列
#print(type(X))
#print(y)
X = np.array(X.values)
y = np.array(y.values)
theta = np.array([0,0]).reshape(1,2)
计算代价函数
def compute_cost(X,y,theta):
#print(t_theta.shape)
inner = np.power(((X.dot(theta.T))-y),2) # 后面的2表示2次幂
return sum(inner)/(2*len(X))
进行梯度下降函数的编写
parameters = int(theta.flatten().shape[0]) # 参数的数量
alpha = 0.01
epoch =100
def gradientDescent(X, y, theta, alpha, epoch=1000):
'''return theta, cost'''
temp = np.array(np.zeros(theta.shape)) # 初始化一个theta临时矩阵
parameters = int(theta.flatten().shape[0]) # 参数theta的数量
cost = np.zeros(epoch) # 初始化一个ndarray,包含每次迭代后的cost
m = X.shape[0] # 样本数量m
for i in range(epoch):
# 利用向量化同步计算theta值
# 注意theta是一个行向量
temp = theta - (alpha/m) * (X.dot(theta.T)- y).T.dot(X) # 得出一个theta行向量
theta = temp
cost[i] = compute_cost(X, y, theta) # 这个函数中,theta是变量,X,y是已知量
return theta,cost # 迭代结束之后返回theta和cost值
本题的梯度下降函数的原理如下图所示,所以在前面的代码中,我们使用data.insert(0, ‘Ones’, 1),在初始样本中插入一列1:
进行计算的过程如下:
final_theta, cost = gradientDescent(X, y, theta, alpha, epoch)
final_cost = compute_cost(X, y, final_theta)
#[4.47802761]
population = np.linspace(data.Population.min(), data.Population.max(), 97)
population.shape
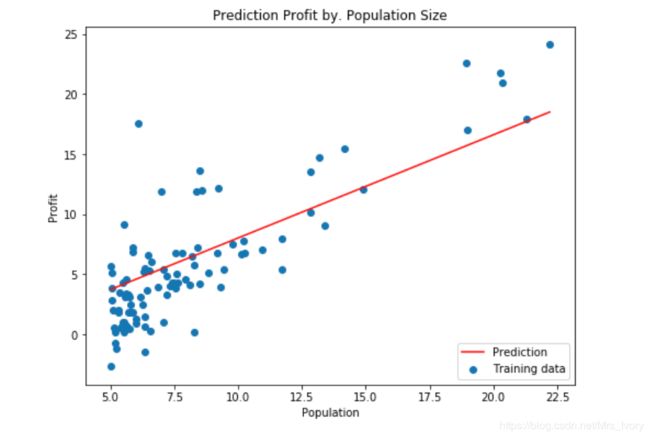
画出拟合的结果图像
population = np.linspace(data.Population.min(), data.Population.max(), 100) # 横坐标
profit = final_theta[0,0] + (final_theta[0,1] * population) # 纵坐标,利润
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(population, profit, 'r', label='Prediction')
ax.scatter(data['Population'], data['Profit'], label='Training data')
ax.legend(loc=4) # 4表示标签在右下角
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Prediction Profit by. Population Size')
plt.show()
多变量线性回归
建议::运行多变量线性回归的时候,新建一个.py文件,不要和上面的单变量在同一文件中,因为对于初学者会出现一些错误。
练习1还包括一个房屋价格数据集,其中有2个变量(房子的大小,卧室的数量)和目标(房子的价格)。 我们使用我们已经应用的技术来分析数据集。
数据集:ex2data.txt
载入数据
path = 'ex2data.txt'
data2 = pd.read_csv(path, names=['Size', 'Bedrooms', 'Price'])
data2.head()
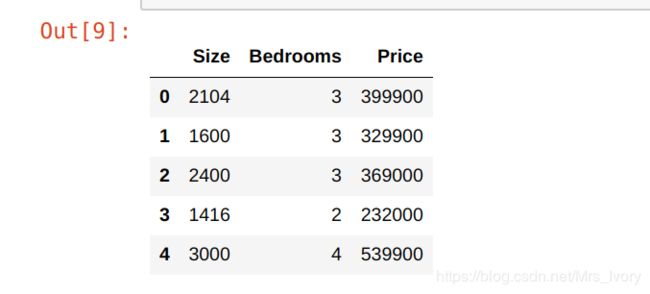
对于此任务,我们添加了另一个预处理步骤 - 特征归一化。因为有两个变量,所以我们必须对数据进行特征归一化
data2 = (data2 - data2.mean()) / data2.std()
data2.head()
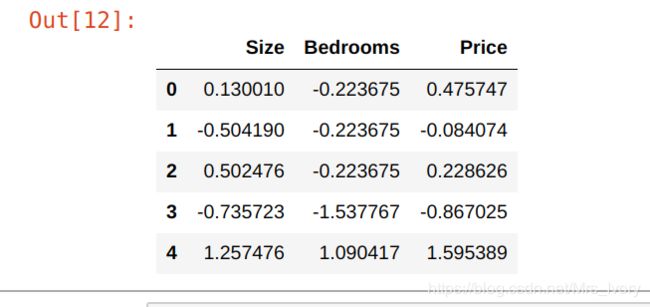
现在我们重复第1部分的预处理步骤,并对新数据集运行线性回归程序。(切记,插入第一列的语句只要运行一次)
# add ones column
# set X (training data) and y (target variable)
data2.insert(0, 'Ones', 1)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]
# convert to matrices and initialize theta
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))
# perform linear regression on the data set
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, epoch)
# get the cost (error) of the model
运行程序。读者是新手,不知如何画出和两个变量的拟合图,故画出了代价函数随着迭代次数的运行函数图
compute_cost(X2, y2, g2), g2
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(epoch), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()