Java学习笔记（23） Sorting

23.1Introduction

The data to be sorted might be integers, doubles,characters, or objects.The Java API contains severaloverloaded sort methods for sorting primitive type values and objects in thejava.util.Arrays andjava.util.Collectionsclasses. For simplicity, this chapter assumes:

1. data to be sorted are integers,

2. data are stored in an array, and

3. data are sorted in ascending order.

The programs can be easily modified to sortother types of data, to sort in descending order, or to sort data in anArrayList or aLinkedList.

23.2Insertion Sort

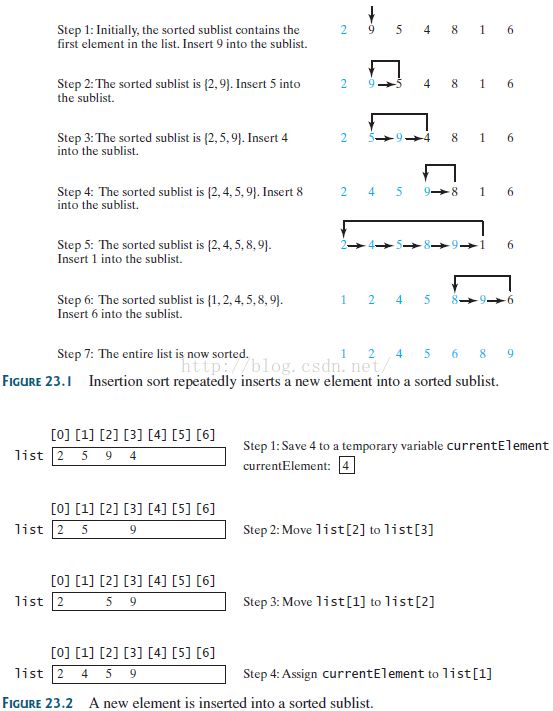
The insertion-sort algorithm sorts a list of values byrepeatedly inserting a new element into a sorted sublist until the whole listis sorted.

LISTING23.1 InsertionSort.java

1 public class InsertionSort {
2	 /** The method for sorting the numbers */
3	 public static void insertionSort(int[] list) {
4 		for (int i = 1; i < list.length; i++) {
5		 /** Insert list[i] into a sorted sublist list[0..i-1] so that
6		 list[0..i] is sorted. */
7		 int currentElement = list[i];
8		 int k;
9		 for (k = i - 1; k >= 0 && list[k] > currentElement; k--) {
10			 list[k + 1] = list[k];
11		 }
12
13		 // Insert the current element into list[k + 1]
14		 list[k + 1] = currentElement;
15		}
16	 }
17}

At the kth iteration, to insert an element into an array of sizek, it may takek comparisons to findthe insertion position, andk moves to insert the element. LetT(n) denote the complexityfor insertion sort andc denote the total number of other operations such asassignments and additional comparisons in each iteration. Thus,

Therefore, the complexity of the insertion sort algorithmis O(n2). Hence, the selection sort and insertion sort are of the same timecomplexity.

23.3 BubbleSort

Abubble sort sorts the array in multiple phases. Each pass successively swapsthe neighboring elements if the elements are not in order.

The bubble sort algorithm makes several passes throughthe array. On each pass, successive neighboring pairs are compared. If a pairis in decreasing order, its values are swapped; otherwise, the values remainunchanged. The technique is called a bubble sort or sinking sort, because thesmaller values gradually “bubble” their way to the top and the larger values sink to thebottom. After the first pass, the last element becomes the largest in thearray. After the second pass, the second-to-last element becomes the secondlargest in the array. This process is continued until all elements are sorted.

LISTING23.2 Bubble SortAlgorithm

1 for (int k = 1; k < list.length; k++) {
2	 // Perform the kth pass
3	 for (int i = 0; i < list.length - k; i++) {
4		 if (list[i] > list[i + 1])
5			 swap list[i] with list[i + 1];
6	 }
7 }

Note that if no swap takes place in a pass, there is noneed to perform the next pass, because all the elements are already sorted. Youcan use this property to improve the algorithm in Listing 23.2 as in Listing23.3.

LiSTING23.3 ImprovedBubble Sort Algorithm

1 boolean needNextPass = true;
2 for (int k = 1; k < list.length && needNextPass; k++) {
3	 // Array may be sorted and next pass not needed
4	 needNextPass = false;
5	 // Perform the kth pass
6	 for (int i = 0; i < list.length – k; i++) {
7		 if (list[i] > list[i + 1]) {
8			 swap list[i] with list[i + 1];
9			 needNextPass = true; // Next pass still needed
10		 }
11	 }
12}

LISTING23.4 BubbleSort.java

1 public class BubbleSort {
2	 /** Bubble sort method */
3	 public static void bubbleSort(int[] list) {
4		 boolean needNextPass = true;
5
6		 for (int k = 1; k < list.length && needNextPass; k++) {
7			 // Array may be sorted and next pass not needed
8			 needNextPass = false;
9			 for (int i = 0; i < list.length - k; i++) {
10				 if (list[i] > list[i + 1]) {
11					 // Swap list[i] with list[i + 1]
12					 int temp = list[i];
13					 list[i] = list[i + 1];
14					 list[i + 1] = temp;
15
16					 needNextPass = true; // Next pass still needed
17				 }
18			 }
19		 }
20	 }
21
22	 /** A test method */
23	 public static void main(String[] args) {
24		 int[] list = {2, 3, 2, 5, 6, 1, -2, 3, 14, 12};
25		 bubbleSort(list);
26		 for (int i = 0; i < list.length; i++)
27			 System.out.print(list[i] + " ");
28		 }
29	 }

 

-2 1 2 2 3 3 5 612 14

 

In the best case, the bubble sort algorithm needs justthe first pass to find that the array is already sorted—no next pass isneeded. Since the number of comparisons is n - 1 in the first pass, thebest-case time for a bubble sort is O(n).

In the worst case, the bubble sort algorithm requires n -1 passes. The first pass makes n - 1