OKapi BM25 算法

BM25（Best Match25）是在信息检索系统中根据提出的query对document进行评分的算法。It is based on the probabilistic retrieval framework developed in the 1970s and 1980s by Stephen E. Robertson, Karen Spärck Jones, and others.BM25算法首先由OKapi系统实现，所以又称为OKapi BM25。

　　

      BM25属于bag-of-words模型，bag-of-words模型只考虑document中词频，不考虑句子结构或者语法关系之类，把document当做装words的袋子，具体袋子里面可以是杂乱无章的。It is not a single function, but actually a whole family of scoring functions, with slightly different components and parameters. One of the most prominent instantiations of the function is as follows.

　　对于一个query , 包括关键字 , 一个文档的BM25得分:

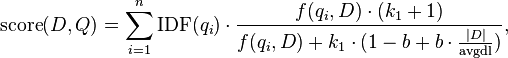
其中IDF是上篇文章《TD-IDF》中的IDF，f是《TD-IDF》中的TF，|D|是文档D的长度，avgdl是语料库全部文档的平均长度。k₁和b是参数。usually chosen, in absence of an advanced optimization, as  and 。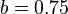

相关性

对每一个搜索查询，我们很容易给每个文档定义一个“相关分数”。当用户进行搜索时，我们可以使用相关分数进行排序而不是使用文档出现时间来进行排序。这样，最相关的文档将排在第一个，无论它是多久之前创建的（当然，有的时候和文档的创建时间也是有关的）。

有很多很多种计算文字之间相关性的方法，但是我们要从最简单的、基于统计的方法说起。这种方法不需要理解语言本身，而是通过统计词语的使用、匹配和基于文档中特有词的普及率的权重等情况来决定“相关分数”。

这个算法不关心词语是名词还是动词，也不关心词语的意义。它唯一关心的是哪些是常用词，那些是稀有词。如果一个搜索语句中包括常用词和稀有词，你最好让包含稀有词的文档的评分高一些，同时降低常用词的权重。

这个算法被称为 Okapi BM25。它包含两个基本概念 词语频率(term frequency) 简称词频(“TF”) 和 文档频率倒数(inverse document frequency) 简写为(“IDF”). 把它们放到一起，被称为 “TF-IDF”，这是一种统计学测度，用来表示一个词语 (term) 在文档中有多重要。

TF-IDF

词语频率( Term Frequency), 简称 “TF”, 是一个很简单的度量标准：一个特定的词语在文档出现的次数。你可以把这个值除以该文档中词语的总数，得到一个分数。例如文档中有 100 个词， ‘the’ 这个词出现了 8 次，那么 ‘the’ 的 TF 为 8 或 8/100 或 8%（取决于你想怎么表示它）。

逆向文件频率（Inverse Document Frequency）, 简称 “IDF”，要复杂一些：一个词越稀有，这个值越高。它由总文件数目除以包含该词语之文件的数目，再将得到的商取对数得到。越是稀有的词，越会产生高的 “IDF”。

如果你将这两个数字乘到一起 (TF*IDF), 你将会得到一个词语在文档中的权重。“权重”的定义是：这个词有多稀有并且在文档中出现的多么频繁？

你可以将这个概念用于文档的搜索查询。在查询中的对于查询中的每个关键字，计算他们的 TF-IDF 分数，并把它们相加。得分最高的就是与查询语句最符合的文档。

很酷吧！

Okapi BM25

上述算法是一个可用的算法，但并不太完美。它给出了一个基于统计学的相关分数算法，我们还可以进一步改进它。

Okapi BM25 是到目前为止被认为最先进的排名算法之一（所以被称为 ElasticSearch ）。Okapi BM25 在 TF-IDF 的基础上增加了两个可调参数，k1 和 b，, 分别代表 “词语频率饱和度（term frequency saturation）” 和 “字段长度规约”。这是什么鬼？

为了能直观的理解“词语频率饱和度”，请想象两篇差不多长度的讨论棒球的文章。另外，我们假设所有文档(除去这两篇)并没有多少与棒球相关的内容，因此 “棒球” 这个词将具有很高的 IDF – 它极稀少而且很重要。 这两篇文章都是讨论棒球的，而且都花了大量的篇幅讨论它，但是其中一篇比另一篇更多的使用了“棒球”这个词。那么在这种情况，是否一篇文章真的要比另一篇文章相差很多的分数呢？既然两个两个文档都是大篇幅讨论棒球的，那么“棒球”这个词出现 40 次还是 80 次都是一样的。事实上，30 次就该封顶啦！

这就是 “词语频率饱和度。原生的 TF-IDF 算法没有饱和的概念，所以出现 80 次“棒球”的文档要比出现 40 次的得分高一倍。有些时候，这时我们所希望的，但有些时候我们并不希望这样。

此外，Okapi BM25 还有个 k1 参数，它用于调节饱和度变化的速率。k1 参数的值一般介于 1.2 到  2.0 之间。数值越低则饱和的过程越快速。（意味着两个上面两个文档有相同的分数，因为他们都包含大量的“棒球”这个词语）

字段长度归约（Field-length normalization）将文档的长度归约化到全部文档的平均长度上。这对于单字段集合（single-field collections）（例如 ours）很有用，可以将不同长度的文档统一到相同的比较条件上。对于双字段集合（例如 “title” 和 “body”）更加有意义，它同样可以将 title 和 body 字段统一到相同的比较条件上。字段长度归约用 b 来表示，它的值在 0 和 1 之间，1 意味着全部归约化，0 则不进行归约化。

算法

在Okapi BM25 维基百科中你可以了解Okapi算法的公式。既然都知道了式子中的每一项是什么，这肯定是很容易地就理解了。所以我们就不提公式，直接进入代码：

BM25.Tokenize = function(text) {
    text = text
        .toLowerCase()
        .replace(/\W/g, ' ')
        .replace(/\s+/g, ' ')
        .trim()
        .split(' ')
        .map(function(a) { return stemmer(a); });

    // Filter out stopStems
    var out = [];
    for (var i = 0, len = text.length; i < len; i++) {
        if (stopStems.indexOf(text[i]) === -1) {
            out.push(text[i]);
        }
    }

    return out;
};

我们定义了一个简单的静态方法Tokenize()，目的是为了解析字符串到tokens的数组中。就这样，我们小写所有的tokens（为了减少熵）。我们运行Porter Stemmer 算法来减少熵的量同时也提高匹配程度（“walking”和”walk”匹配是相同的）。而且我们也过滤掉停用词（很普通的词）为了更近一步减少熵值。在我所写的概念深入之前，如果我过于解释这一节就请多担待。

BM25.prototype.addDocument = function(doc) {
    if (typeof doc.id === 'undefined') { throw new Error(1000, 'ID is a required property of documents.'); };
    if (typeof doc.body === 'undefined') { throw new Error(1001, 'Body is a required property of documents.'); };

    // Raw tokenized list of words
    var tokens = BM25.Tokenize(doc.body);

    // Will hold unique terms and their counts and frequencies
    var _terms = {};

    // docObj will eventually be added to the documents database
    var docObj = {id: doc.id, tokens: tokens, body: doc.body};

    // Count number of terms
    docObj.termCount = tokens.length;

    // Increment totalDocuments
    this.totalDocuments++;

    // Readjust averageDocumentLength
    this.totalDocumentTermLength += docObj.termCount;
    this.averageDocumentLength = this.totalDocumentTermLength / this.totalDocuments;

    // Calculate term frequency
    // First get terms count
    for (var i = 0, len = tokens.length; i < len; i++) {
        var term = tokens[i];
        if (!_terms[term]) { 
            _terms[term] = {
                count: 0,
                freq: 0
            }; 
        };
        _terms[term].count++;
    }

    // Then re-loop to calculate term frequency.
    // We'll also update inverse document frequencies here.
    var keys = Object.keys(_terms);
    for (var i = 0, len = keys.length; i < len; i++) {
        var term = keys[i];
        // Term Frequency for this document.
        _terms[term].freq = _terms[term].count / docObj.termCount;

        // Inverse Document Frequency initialization
        if (!this.terms[term]) {
            this.terms[term] = {
                n: 0, // Number of docs this term appears in, uniquely
                idf: 0
            };
        }

        this.terms[term].n++;
    };

    // Calculate inverse document frequencies
    // This is SLOWish so if you want to index a big batch of documents,
    // comment this out and run it once at the end of your addDocuments run
    // If you're only indexing a document or two at a time you can leave this in.
    // this.updateIdf();

    // Add docObj to docs db
    docObj.terms = _terms;
    this.documents[docObj.id] = docObj;
};

这就是addDocument()这种方法会奇迹般出现的地方。我们基本上建立和维护两个类似的数据结构:this.documents.和this.terms。

this.documentsis 是一个保存着所有文档的数据库，它保存着文档的全部原始文字，文档的长度信息和一个列表，列表里面保存着文档中的所有词语和词语的数量与出现频率。使用这个数据结构，我们可以很容易的和快速的（是的，非常快速，只需要时间复杂度为O(1)的哈表查询时间）回答如下问题：在文档 #3 中，’walk’ 这个词语出现了多少次？

我们在还使用了另一个数据结构，this.terms。它表示语料库中的所有词语。通过这个数据结构，我们可以在O(1)时间内回答如下问题：’walk’ 这个词在多少个文档中出现过？他们的 id 是什么？

最后，我们记录了每个文档的长度，并记录了整个语料库中文档的平均长度。

注意，上面的代码中， idf 被初始化 0，而且 updateidf() 方法被注释掉了。这是因为这个方法运行的非常慢，并且只需在建立索引之后运行一次就可以了。既然运行一次就能满足需求，就没有必要运行5000次。先把它注释掉，然后在大批量的索引操作之后运行，就可以节省很多时间。下面是这个函数的代码：

BM25.prototype.updateIdf = function() {
    var keys = Object.keys(this.terms);
    for (var i = 0, len = keys.length; i < len; i++) {
        var term = keys[i];
        var num = (this.totalDocuments - this.terms[term].n + 0.5);
        var denom = (this.terms[term].n + 0.5);
        this.terms[term].idf = Math.max(Math.log10(num / denom), 0.01);
    }
};

这是一个非常简单的函数，但是由于它需要遍历整个语料库中的所有词语，并更新所有词语的值，这就导致它工作的就有点慢。这个方法的实现采用了逆向文档频率 (inverse document frequency) 的标准公式（你可以在 Wikipedia 上找到这个公式）—  由总文件数目除以包含该词语之文件的数目，再将得到的商取对数得到。我做了一些修改，让返回值一直大于0。

BM25.prototype.search = function(query) {

    var queryTerms = BM25.Tokenize(query);
    var results = [];

    // Look at each document in turn. There are better ways to do this with inverted indices.
    var keys = Object.keys(this.documents);
    for (var j = 0, nDocs = keys.length; j < nDocs; j++) {
        var id = keys[j];
        // The relevance score for a document is the sum of a tf-idf-like
        // calculation for each query term.
        this.documents[id]._score = 0;

        // Calculate the score for each query term
        for (var i = 0, len = queryTerms.length; i < len; i++) {
            var queryTerm = queryTerms[i];

            // We've never seen this term before so IDF will be 0.
            // Means we can skip the whole term, it adds nothing to the score
            // and isn't in any document.
            if (typeof this.terms[queryTerm] === 'undefined') {
                continue;
            }

            // This term isn't in the document, so the TF portion is 0 and this
            // term contributes nothing to the search score.
            if (typeof this.documents[id].terms[queryTerm] === 'undefined') {
                continue;
            }

            // The term is in the document, let's go.
            // The whole term is :
            // IDF * (TF * (k1 + 1)) / (TF + k1 * (1 - b + b * docLength / avgDocLength))

            // IDF is pre-calculated for the whole docset.
            var idf = this.terms[queryTerm].idf;
            // Numerator of the TF portion.
            var num = this.documents[id].terms[queryTerm].count * (this.k1 + 1);
            // Denomerator of the TF portion.
            var denom = this.documents[id].terms[queryTerm].count 
                + (this.k1 * (1 - this.b + (this.b * this.documents[id].termCount / this.averageDocumentLength)));

            // Add this query term to the score
            this.documents[id]._score += idf * num / denom;
        }

        if (!isNaN(this.documents[id]._score) && this.documents[id]._score > 0) {
            results.push(this.documents[id]);
        }
    }

    results.sort(function(a, b) { return b._score - a._score; });
    return results.slice(0, 10);
};

最后，search() 方法遍历所有的文档，并给出每个文档的 BM25 分数，然后按照由大到小的顺序进行排序。当然了，在搜索过程中遍历语料库中的每个文档实是不明智。这个问题在 Part Two （反向索引和性能）中得到解决。

上面的代码已经做了很好的注释，其要点如下：为每个文档和每个词语计算 BM25 分数。词语的 idf 分数已经预先计算好了，使用的时候只需要查询即可。词语频率作为文档属性的一部分也已经预先计算好了。之后只需要简单的四则运算即可。最后给每个文档增加一个临时变量 _score，然后根据 score 做降序排列并返回前 10 个结果。

示例，源代码，注意事项和下一步计划

上面的示例有很多方法进行优化，我们将在 “全文搜索”的第二部分中介绍它们，欢迎继续收看。我希望我能在几个星期之后完成它。下面列了下次将要提到的内容：

• 反向索引和快速搜索
• 快速索引
• 更好的搜索结果

为了这个演示，我编了一个小的维基百科爬虫，爬到相当多（85000）维基百科文章的第一段。由于索引到所有85K文件需要90秒左右，在我的电脑我已经削减了一半。不想让你们仅仅为了一个简单的全文本演示浪费你的笔记本电脑电量。

因为索引是一个繁重的、模块化的CPU操作，我把它当成一个网络工作者。索引运行在一个后台线程上–在这里你可以找到完整的源代码。你也会发现到词干算法和我的停用词列表中的源代码参考。至于代码许可，还是一如既往为教育目的而免费，而不用于任何商业目的。

最后是演示。一旦索引完成，尝试寻找随机的东西和短语，维基百科会知道的。注意，只有40000段的索引，所以你可能要尝试一些新的话题。