KMeans聚类,GMM算法,EM算法通俗详解
首先推荐两个链接
1 刘建平博客园:https://www.cnblogs.com/pinard/category/894692.html【具体内容自行查看】
2,来自sklearn官方文档的一段叙述:
Gaussian mixture models, useful for clustering, are described in another chapter of the documentation dedicated to mixture models. KMeans can be seen as a special case of Gaussian mixture model with equal covariance per component.
注:本文基本没有公式推导,写这篇博客的起因是我注意到一些机器学习算法岗位面试提到了GMM与KMeans聚类算法的联系,另外GMM里面主要使用了EM算法思想,我索性就拿到一块来讲。
KMeans聚类
通俗理解:有10w个无标签样本,假设它们分为k个类(当然你并不知道,这k个类具体怎么分布,每个类的特征是什么)。那么问题来了,该怎么把这无标签的样本分成k个类呢-----> 物以类聚,人以群分。打个比方,如果咱们两人聊得来,那么我们之间肯定存在共同语言,也就是我们之间相似之处有很多:我们之间的特征距离相比其他人而言更近。在数学当中这个距离一般用欧几里得距离表示,原始KMeans就是通过计算观测值之间的距离进行比较,找出距离最小的那一部分并将其归为一类:具体算法步骤可以参阅 周志华机器学习P202 或者github代码
注:实际当中一般讲样本属性进行编码成为特征向量,在进行距离计算 一般有one-hot编码
其次了解一下混合模型(Mixture Model)
#A,General mixture model(常规混合模型,有限维度的层次模型 hierarchical model)有以下属性:
1,N random variables that are observed, each distributed according to a mixture of K components, with the components belonging to the same parametric family of distributions (e.g., all normal, all Zipfian, etc.) but with different parameters(N个已知的随机变量,都服从于一个混合模型(大模型),此模型包含k个分布模型(小模型),每个模型都是已知的并且属于同一种类但参数不同)
2,N random latent variables specifying the identity of the mixture component of each observation, each distributed according to a K-dimensional categorical distribution(N个随机隐变量确定了已知随机变量的分布特征,也就是隐变量明确的告诉你 第i个观察到的随机变量/第i个观测值属于哪个混合模型中的哪个小模型)
3,A set of K mixture weights, which are probabilities that sum to 1(每个小模型的权重之和为1: ∑ k = 1 \sum_k = 1 ∑k=1)
4, A set of K parameters, each specifying the parameter of the corresponding mixture component. In many cases, each “parameter” is actually a set of parameters. For example, if the mixture components are Gaussian distributions, there will be a mean and variance for each component. (每个小模型里的参数都确定了这个小模型的特征,事实上这里说的参数有可能是参数的集合,例如高斯分布的参数是均值和方差(协方差)的集合)
5,一般整个混合模型数学表示及结构如下
| 名称 | 含义 |
|---|---|
| K | number of mixture models(小模型的个数) |
| N | number of observations(随机变量/观测值的个数 ) |
| θ i = 1... k \theta_{i=1...k} θi=1...k | parameters of distribution of observation associated with components i (小模型的参数) |
| α i = 1... k \alpha_{i=1...k} αi=1...k | mixture weight,i.e…,prior probability of particular component i(小模型的权重/先验分布) |
| y i = 1... N y_{i=1...N} yi=1...N | observation i(已知随机变量[观测值/样本值]) |
| P ( y / θ ) P(y/\theta) P(y/θ) | probability distribution of an observation,parametrized on θ \theta θ ( θ \theta θ参数下的概率分布) |
#B,GMM便是常规混合模型中小模型种类是高斯分布的特例 参数 θ \theta θ是均值 μ i \mu_i μi和方差 σ i 2 \sigma_i^2 σi2,即 θ i \theta_i θi = { μ i , σ i 2 } \left\{\mu_i, \sigma_i^2 \right\} {μi,σi2},高斯混合模型可表示为: P ( y ∣ θ ) = ∑ k = 1 K α k ϕ ( y ∣ θ k ) P(y|\theta) = \sum_{k=1}^{K}\alpha_k\phi\left( y|\theta_k \right) P(y∣θ)=∑k=1Kαkϕ(y∣θk)。
其中 θ = ( α 1 , α 2 , . . . α k ; θ 1 , θ 2 , . . . θ k ) θ=\left( \alpha_1,\alpha_2,...\alpha_k;\theta_1,\theta_2,...\theta_k \right) θ=(α1,α2,...αk;θ1,θ2,...θk), 然后利用EM算法估计高斯混合模型的参数 θ θ θ,
那么对应EM算法中的隐变量是什么:反映观测数据 y i y_i yi是来自第k个小模型是未知的,用 γ i k \gamma_{ik} γik表示,其定义很简单,如下
γ i k = { 1 , 第 i 个 观 测 值 来 自 第 k 个 小 模 型 0 , 否 则 \gamma_{ik}= \begin{cases} 1, &第i个观测值来自第k个小模型\\ 0, & 否则 \end{cases} γik={1,0,第i个观测值来自第k个小模型否则 i = 1,2,…N;k = 1,2,…,K; γ i k \gamma_{ik} γik是0,1随机变量
下面的公式推导我不再叙述,读者可翻阅 统计学习方法P163
通俗理解:GMM它也是在不断的通过EM迭代寻找最佳参数 θ \theta θ来将整个观测样本进行分割在通过权重 α \alpha α组合成为混合模型;废话不多说先上图了解一下优化过程
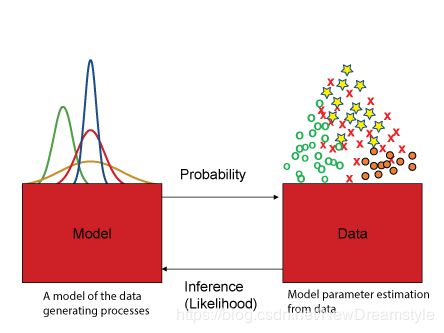

与KMeans一样,先初始化参数:
我们先假设这是有标签的观测值
先随便猜一组参数,然后将观测值扔进去得出第一次模型,你会发现跟标签概率分布误差较大,接下来再调整参数得到更好的模型,这样一步一步迭代下去直至误差最小。
当然我们得讨论聚类无监督学习,不存在已知的标签,所以你无法根据以往监督学习的误差函数来进行一个优化,这个时候便想到了EM算法
----------------------------------------------------------------------------5.21分割线-----------------------------------------
十几天前写的一直忙就存为草稿没动,准备接下来写EM算法的详解,先发布再说然后慢慢添加就当做一种督促