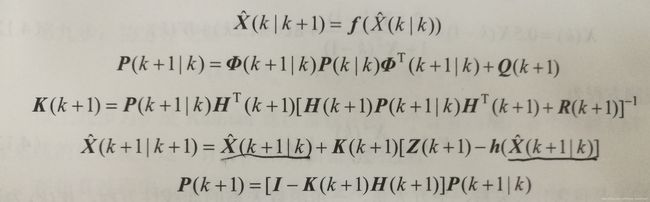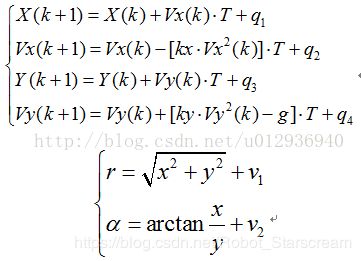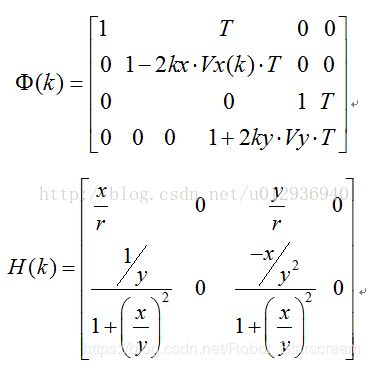「滤波算法」“扩展卡尔曼滤波（EFK）实例”讲解

本文将https://blog.csdn.net/u012936940/article/details/77249245进行了优化讲解。

---

1.应用的系统模型：

                                    

2.在扩展卡尔曼滤波中，状态的预测以及观测值的预测由非线性函数计算得出，线性卡尔曼滤波中的状态转移矩阵 A 阵和观测矩阵 H 阵由  和  函数的雅克比矩阵代替，假设状态有n维，则求法如下：

3.扩展卡尔曼滤波与线性卡尔曼滤波过程相同，五个公式如下：

                       

*为了方便表示两个雅可比公式，设出了  和 .

4.实例     

（1）根据图中情景，选取横向位置、速度，纵向位置、速度为状态量，列出下面非线性状态方程及观测方程

（2）根据状态方程和观测方程，提前计算雅克比矩阵如下：

（3）Matlab实现

close all;
clear all;
%%  真实轨迹（模拟）
kx = 0.01;   ky = 0.05;     % 阻尼系数
g = 9.8;                    % 重力
t = 15;                     % 仿真时间
Ts = 0.1;                   % 采样周期 
len = fix(t/Ts);            % 仿真步数
dax = 0.3; day = 0.3;       % 系统噪声
X = zeros(len,4);           % 状态的空矩阵
X(1,:) = [0, 50, 500, 0];   % 状态模拟的初值
for k=2:len
    x = X(k-1,1); vx = X(k-1,2); y = X(k-1,3); vy = X(k-1,4); 
    x = x + vx*Ts;
    vx = vx + (-kx*vx^2+dax*randn(1,1))*Ts;
    y = y + vy*Ts;
    vy = vy + (ky*vy^2-g+day*randn(1))*Ts;
    X(k,:) = [x, vx, y, vy];
end
%%  构造雷达测量值
dr = 8;  dafa = 0.1;        % 测量噪声
for k=1:len
    r = sqrt(X(k,1)^2+X(k,3)^2) + dr*randn(1,1);
    a = atan(X(k,1)/X(k,3))*57.3 + dafa*randn(1,1);
    Z(k,:) = [r, a];
end
%% EKF 扩展卡尔曼滤波
Qk = diag([0; dax; 0; day])^2;  
Rk = diag([dr; dafa])^2;        %W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise)，他们的协方差(covariance)分别是Q，R（这里我们假设他们不随系统状态变化而变化）
Pk = 10*eye(4);                 %卡尔曼增益
Pkk_1 = 10*eye(4);              %状态协方差矩阵
x_hat = [0,40,400,0]';          %最优状态过程变量
X_est = zeros(len,4);           %最优的状态
x_forecast = zeros(4,1);        %预测的状态矩阵
z = zeros(4,1);                 %观测矩阵
for k=1:len
    % 1 状态预测    
    x1 = x_hat(1) + x_hat(2)*Ts;
    vx1 = x_hat(2) + (-kx*x_hat(2)^2)*Ts;
    y1 = x_hat(3) + x_hat(4)*Ts;
    vy1 = x_hat(4) + (ky*x_hat(4)^2-g)*Ts;
    x_forecast = [x1; vx1; y1; vy1];        %预测值
    % 2  观测预测
    r = sqrt(x1*x1+y1*y1);
    alpha = atan(x1/y1)*57.3;  %57.3=180/pi,matlab用弧度不用角度
    y_yuce = [r,alpha]';
    %  状态 协方差矩阵（雅可比矩阵）
    vx = x_forecast(2);  vy = x_forecast(4);
    F = zeros(4,4);
    F(1,1) = 1;  F(1,2) = Ts;
    F(2,2) = 1-2*kx*vx*Ts;
    F(3,3) = 1;  F(3,4) = Ts;
    F(4,4) = 1+2*ky*vy*Ts;
    Pkk_1 = F*Pk*F'+Qk;
    %观测 协方差矩阵（雅可比矩阵）
    %观测方程的雅克比矩阵是观测量对状态量求导，这里观测量有距离和角度，状态有4个量，每一个观测量分别对4个状态求导，最终这里的雅克比矩阵是2x4的矩阵。
    x = x_hat(1); y = x_hat(3);
    H = zeros(2,4);
    r = sqrt(x^2+y^2);  xy2 = 1+(x/y)^2;
    H(1,1) = x/r;  H(1,3) = y/r;
    H(2,1) = (1/y)/xy2;  H(2,3) = (-x/y^2)/xy2;
    %计算卡尔曼增益
    Kk = Pkk_1*H'*(H*Pkk_1*H'+Rk)^-1;
    %校正
    x_hat = x_forecast+Kk*(Z(k,:)'-y_yuce);      
    Pk = (eye(4)-Kk*H)*Pkk_1;
    X_est(k,:) = x_hat;
end
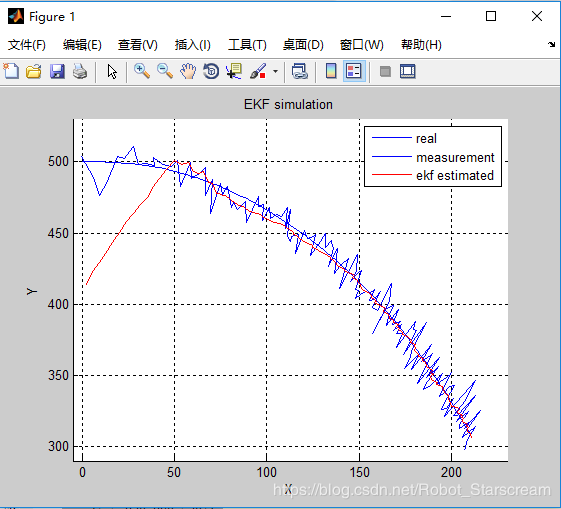
%%绘图 
figure, hold on, grid on;
plot(X(:,1),X(:,3),'-b');    %真实位置
plot(Z(:,1).*sin(Z(:,2)*pi/180), Z(:,1).*cos(Z(:,2)*pi/180));   %观测位置
plot(X_est(:,1),X_est(:,3), 'r');   %最优位置
xlabel('X'); 
ylabel('Y'); 
title('EKF simulation');
legend('real', 'measurement', 'ekf estimated');
axis([-5,230,290,530]);

（4）Matlab仿真结果