关于AVL（二叉平衡树）的插入讲解，很简单

AVL又称二叉平衡树，是会自平衡的二叉搜索树，左孩子比自己小，右孩子比自己大，关键在于他的每一个节点左右孩子高度差绝对值不会超过1
实际上我上网查了好几次AVL的详解，关于里面怎么平衡，单左，单右，左右双旋，右左双旋，是知道怎么转的，但那唯一一点删除啃了好几次没啃动。这次天梯赛选拔赛练习题里面有一道AVL插入题，就先把插入这块给捋一捋吧。
插入这块实际上不难，都是几个简单的函数（左转右转之类的）合到一起罢了，在写几个判断条件判断怎么转而已。

树的构造是这样的

struct TNode
{
	int data;
	struct TNode *Left;
	struct TNode *Right;
};

三个元素，一个存数据，一个左孩子指针，一个右孩子指针。

在讲AVL之前我们先要弄懂一个树的取高函数，使用递归来取得树的高度，代码是这样的

int getHight(struct TNode *A)
{
	if (A == NULL)//递归出口
		return 0;
	int LH = getHight(A->Left);
	int RH = getHight(A->Right);
	int MAX = max(LH, RH);
	return MAX + 1;
}

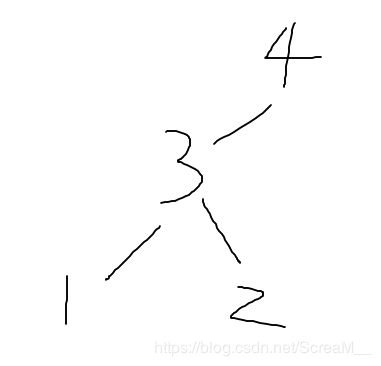
如上图这个树，要求4这个节点的高度，会先一直访问左孩子，直到1的左孩子（NULL）后返回0，此时1节点的左高度为0，之后访问右孩子后返回右高度也为0。之后会取两者的最大值+1返回，回到了节点3，这是节点3的左高是1，访问右孩子后得到右高度也为1，取最大值+1返回最初的4节点。得到4的左高为2，右高为0，最后返回4节点的树高为2+1=3。

在学会了取树高函数后我们就可以开始写AVL了，首先AVL要旋转的条件就是左右孩子的高度差的绝对值等于2.当这个条件成立之后就会开始平衡
平衡有两种，一种是旋转一次的单旋，一种是旋转两次的双旋，而单旋双旋又分别有两个，所以四个旋转分别是左单旋，右单旋，左右双旋，右左双旋。
听起来很多种情况，但事实上，我们只要弄明白一个单旋就自然明白剩下的情况了。

单旋

首先左单旋（顺时针）

实际上我的左单旋是AVL中右旋（顺时针），只不过我都是通过左右孩子谁需要旋转来记X旋

上面这个树，4节点的左孩子高度为2，右孩子高度为0，两者差的绝对值为2，符合平衡条件，因为左边的孩子比较沉，并且最后造成不平衡的那个插入（节点1）比发现不平衡点（节点4）的左孩子（节点3）要小，这种情况只要旋转一次就可以解决，只要把3节点作为根节点，就平衡了

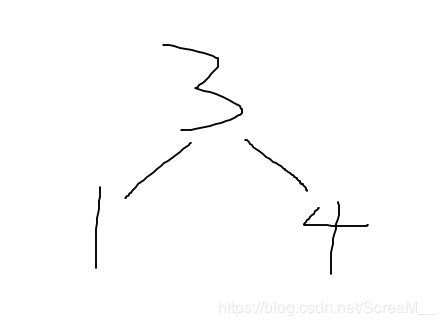
代码是这样的

struct TNode * SL(struct TNode *A)//单左旋(顺时针平衡)
{
	struct TNode * B = A->Left;
	A->Left = B->Right;
	B->Right = A;
	return B;
}

非常简单，用一句话来说就是让4节点的左孩子连接3的右孩子，然后3的右孩子再连接4来平衡。
由于3的右孩子是空的，所以4节点的左孩子就没东西了
而右旋（逆时针向左旋转）也是同理

struct TNode * SR(struct TNode *A)//单右旋(逆时针平衡)
{
	struct TNode * B = A->Right;
	A->Right = B->Left;
	B->Left = A;
	return B;
}

这次是让4右手去抓5的左手（为空），然后5的左手反过来抓4平衡。
这就是所有的单旋情况，剩下的双旋实际上就是进行两次单旋而已

双旋

下图5节点的左孩子高度为2，右孩子高度为0，符合情况。

而最后一次造成不平衡的节点4是大于节点5的左孩子2的，这种情况就要进行双旋，先让2进行一次右旋（逆时针左旋转），然后再让5进行一次左旋（顺时针右旋转）。
再强调一遍我的左右旋是左孩子旋转和右孩子旋转，而不是旋转方向

你会发现，在左右双旋的单右旋平衡后，就又会变成之前单旋的左旋情况，再进行一次单左旋即可。

struct TNode * DLR(struct TNode *A)//左右双旋
{
	A->Left = SR(A->Left);
	return SL(A);
}

代码比单旋还简单，事实上只是进行了两次单旋而已。

struct TNode * DRL(struct TNode *A)//右左双旋
{
	A->Right = SL(A->Right);
	return SR(A);
}

如何判断

那么这有四种情况，到底什么时候该怎么旋转呢。下面来说一下我自己的理解（轻喷）
首先平衡条件，当检测到左右孩子高度差绝对值为2时，就需要旋转了
而这时，如果左孩子比较重，那么需要的就是左单旋或者左右双旋
判断单双旋条件，如果左孩子较重，那么插入的数如果比左孩子小，就单旋，反之则双旋

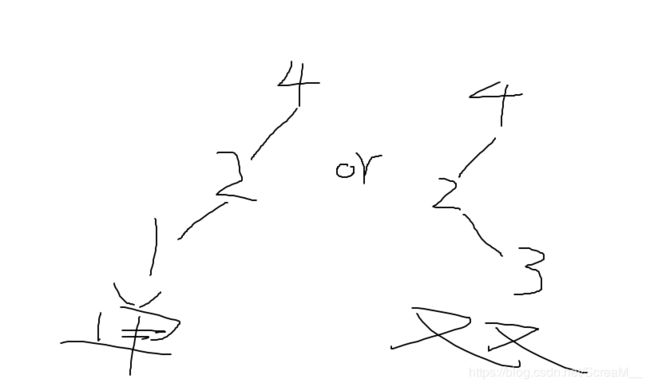
字太丑了！！
你可以发现，如果左孩子重，插入的数（节点1）比左孩子（节点2）还小的话，则是单旋，如果插入（节点3）就是双旋。

插入

以下都是个人理解，我是这么记插入检测平衡的条件的。
实际上插入跟二叉搜索树几乎一样，唯一的不同就是插入完之后，需要检测树高，然后判断是否要平衡（左右孩子高度差绝对值为2）。
在左孩子插入结束后，左边一定会比较高（上图无论插入3还是1,4的左高都是2），就需要左单旋或者左右双旋（都是左）。
左边重，就比较左孩子（2）跟插入数（1或者3）的大小，来决定单旋双旋（1单旋，3双旋）。
反过来右边重，就需要比较右孩子跟插入数的大小，然后决定单旋双旋。
下面是代码

struct TNode * Insert(struct TNode * A,int DATA)//插入
{
	if (A == NULL)
	{
		A = new TNode;
		A->data = DATA;
		A->Left = NULL;
		A->Right = NULL;
	}
	else
	{
		if (A->data > DATA)
		{
			A->Left = Insert(A->Left, DATA);
			if (getHight(A->Left) - getHight(A->Right) == 2)//左插后检测左边是不是超重
			{
				if (A->Left->data > DATA)//左超重判断左孩子与插入数大小决定单旋双旋
					A = SL(A);
				else
					A = DLR(A);
			}
		}
		else if (A->data < DATA)
		{
			A->Right = Insert(A->Right, DATA);
			if (getHight(A->Left) - getHight(A->Right) == -2)//右插后检测右边是否超重
			{
				if (A->Right->data < DATA)//右超重判断右孩子与插入数大小决定单旋双旋
					A = SR(A);
				else
					A = DRL(A);
			}
		}
	}
	return A;
}

下面是一道例题

7-4 平衡二叉树的根 （25 分）
将给定的一系列数字插入初始为空的AVL树，请你输出最后生成的AVL树的根结点的值。
输入格式:
输入的第一行给出一个正整数N（≤20），随后一行给出N个不同的整数，其间以空格分隔。
输出格式:
在一行中输出顺序插入上述整数到一棵初始为空的AVL树后，该树的根结点的值。
输入样例1:
5
88 70 61 96 120
输出样例1:
70
输入样例2:
7
88 70 61 96 120 90 65
输出样例2:
88

直接上代码，然后用样例2来捋一下过程。

#include
#include
using namespace std;
struct TNode
{
	int data;
	struct TNode *Left;
	struct TNode *Right;
};
int getHight(struct TNode *A)
{
	if (A == NULL)
		return 0;
	int LH = getHight(A->Left);
	int RH = getHight(A->Right);
	int MAX = max(LH, RH);
	return MAX + 1;
}
struct TNode * SL(struct TNode *A)//单左旋(顺时针平衡)
{
	struct TNode * B = A->Left;
	A->Left = B->Right;
	B->Right = A;
	return B;
}
struct TNode * SR(struct TNode *A)//单右旋(逆时针平衡)
{
	struct TNode * B = A->Right;
	A->Right = B->Left;
	B->Left = A;
	return B;
}
struct TNode * DLR(struct TNode *A)//左右双旋
{
	A->Left = SR(A->Left);
	return SL(A);
}
struct TNode * DRL(struct TNode *A)//右左双旋
{
	A->Right = SL(A->Right);
	return SR(A);
}
struct TNode * Insert(struct TNode * A,int DATA)//插入
{
	if (A == NULL)
	{
		A = new TNode;
		A->data = DATA;
		A->Left = NULL;
		A->Right = NULL;
	}
	else
	{
		if (A->data > DATA)
		{
			A->Left = Insert(A->Left, DATA);
			if (getHight(A->Left) - getHight(A->Right) == 2)
			{
				if (A->Left->data > DATA)
					A = SL(A);
				else
					A = DLR(A);
			}
		}
		else if (A->data < DATA)
		{
			A->Right = Insert(A->Right, DATA);
			if (getHight(A->Left) - getHight(A->Right) == -2)
			{
				if (A->Right->data < DATA)
					A = SR(A);
				else
					A = DRL(A);
			}
		}
	}
	return A;
}
int main()
{
	struct TNode * A = NULL;
	int n, temp;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> temp;
		A = Insert(A, temp);
	}
	cout << A->data << endl;
	return 0;
}

样例2输入：88 70 61 96 120 90 65
在刚开始插入80、70之后没什么影响，因为根节点左孩子高度最多也就是1，达不到平衡条件。而当插入61之后，变成了这个情况

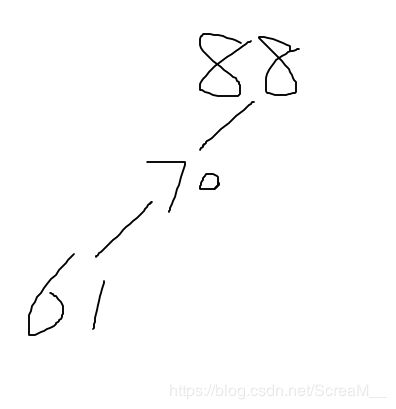
在插入61之后，对70的左孩子高度检测（因为是左插入）是1之后递归回节点88，发现左孩子高度为2（左插入后），开始判断61和左孩子70的大小决定单双旋，发现是单左旋，旋转后

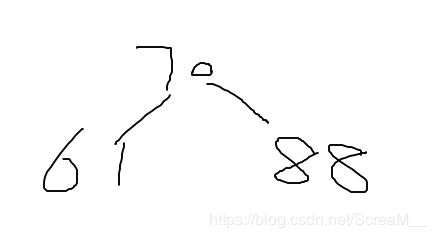
继续插入96，此时根节点右孩子高2，左孩子高1，仍然平衡

继续插入120，插入完之后一直递归检查，到88时发现右插入后造成了不平衡情况，判断单双旋为单旋（120大于96）准备进行右单旋

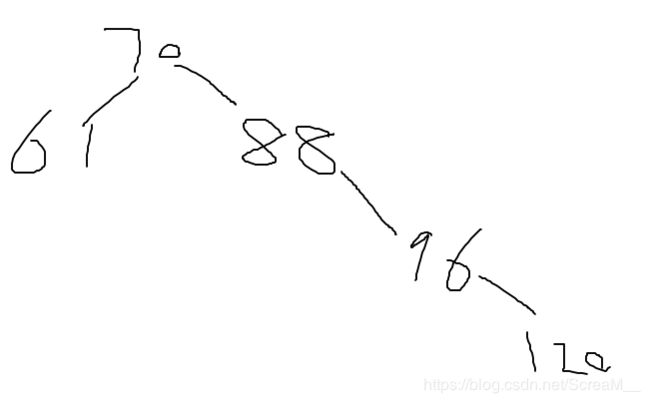
右单旋之后为这样

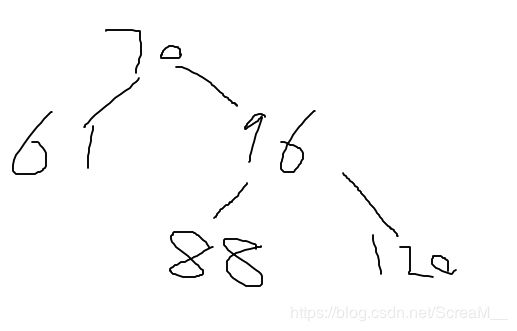
此时的70根就是样例1的答案，我们样例2继续插入90，插入完毕后是这样的

插入完90后，递归检测高度，一直到根节点70发现不平衡（左高1，右高3）
需要右单旋或者右双旋，发现90小于右孩子96，属于右左双旋
先对右孩子96进行左单旋（96左连90，88右连96）后是这样的

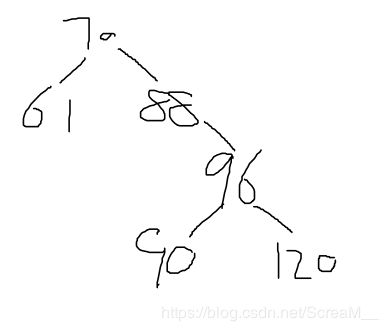
之后再对70进行右单旋（左右双旋连续进行两次单旋）（70右连88左，88左连70）
完成后如图

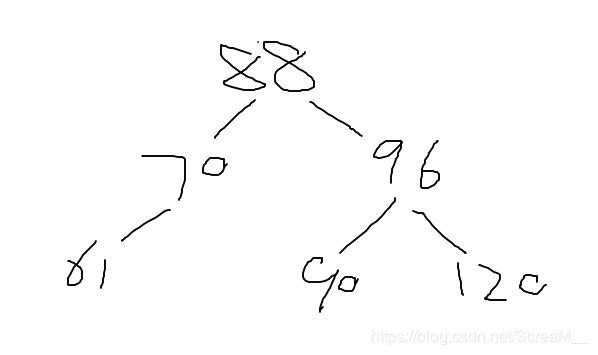
可以看到，经过左右双旋后，树又回到了平衡状态，此时树根为88，最后插入65，不影响平衡，输出结果88。