吴恩达机器学习第六周测验及编程作业和选做题
代码:https://github.com/LiuZhe6/AndrewNGMachineLearning
文章目录
- 测验1:Advice for Applying Machine Learning
- 第一题
- 第二题
- 第三题
- 第四题
- 第五题
- 编程作业:Regularized Linear Regression and Bias/Variance
- 作业一:Regularized Linear Regression Cost Function
- 作业二:Regularized Linear Regression Gradient
- 作业三:Learning Curve
- 作业四:Polynomial Feature Mapping
- 作业五:Validation Curve
- 选做题一:Computing test set error
- 选做二:Plotting learning curves with randomly selected examples
- 测验2:Machine Learning System Design
- 第一题
- 第二题
- 第三题
- 第四题
- 第五题
测验1:Advice for Applying Machine Learning
第一题
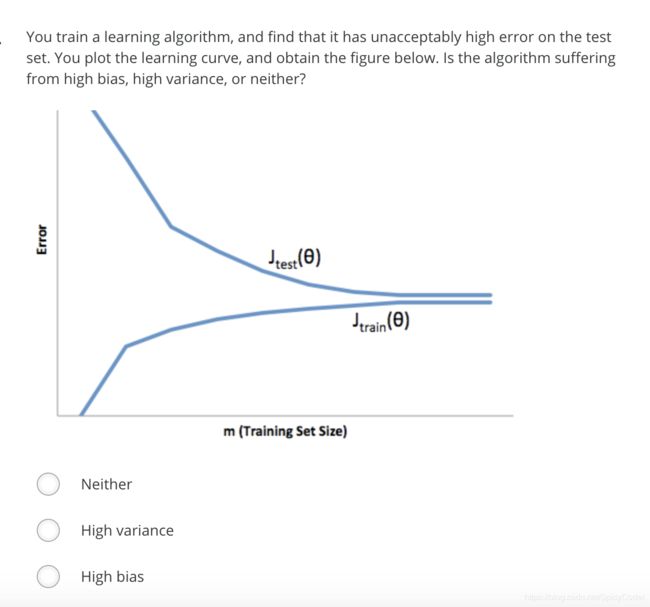
答案
C
分析:测试集误差与训练集误差趋于一致,此时应为高偏差。
第二题

答案
CD
分析:根据题目,假设函数在训练集上表现非常好,但是泛化能力不行,很有可能发生了高方差(过拟合),此时可以采取的措施有:1.减少特征数量 2.增加正则化参数lamda
第三题

答案
AB
分析:根据题目,假设函数在训练集和交叉验证集上表现都不好,故为高偏差(欠拟合),此时可以采取的措施有:1.增加多项式 2.减少正则化参数lamda。
第四题
第五题

答案
ACD
分析:
A:采用学习曲线可以帮助我们更好的了解当前所选择的学习算法的好坏,正确。
B:高偏差和高方差都不好,错误。
C:处于高偏差的情况下,增加训练样本并不一定可以帮助提升效果,正确。
D:处于高方差的情况下,增加训练样本可能帮助提升效果,正确。
编程作业:Regularized Linear Regression and Bias/Variance
作业一:Regularized Linear Regression Cost Function
linearRegCostFunction.m
记得正则化时,theta0不惩罚
J = 1 / (2 * m) * (X * theta - y)' * (X * theta - y) + lambda / (2 * m) * ((theta') * theta - theta(1)^2 );
作业二:Regularized Linear Regression Gradient
linearRegCostFunction.m
grad = 1/m * X' *(X * theta - y) + lambda / m * theta;
grad(1) -= lambda/m * theta(1);
作业三:Learning Curve
learningCurve.m
% 因为需要得到随m的增大,两个误差的值,故需要for循环
for i = 1 : m
theta = trainLinearReg(X(1:i,:), y(1:i) ,lambda);
error_train(i) = linearRegCostFunction(X(1:i,:), y(1:i), theta, 0); %lambda设置为0
error_val(i) = linearRegCostFunction(Xval, yval,theta,0);
作业四:Polynomial Feature Mapping
polyFeatures.m
for i = 1 : p
X_poly(:,i) = X.^i;
end;
作业五:Validation Curve
validationCurve.m
for i = 1 : length(lambda_vec)
lambda = lambda_vec(i);
theta = trainLinearReg(X,y,lambda);
error_train(i) = linearRegCostFunction(X,y,theta,0);
error_val(i) = linearRegCostFunction(Xval,yval,theta,0);
end;
刚开始写error_train和error_val的时候,后面穿的参数写成了lambda,提交发现不对。我思考了一下,觉得这里计算代价的时候,只是针对theta做不同的改变就可以了,lambda始终是0 。因为在上面计算theta的时候,就已经考虑了lambda。
选做题一:Computing test set error
ex5.m
%% 选做部分1:使用最优lambda计算test error
lambda = 3;
theta = trainLinearReg(X_poly,y,lambda);
test_error = linearRegCostFunction(X_poly_test,ytest,theta,0);
打印test_error,可以看到结果为test_error = 3.8599
选做二:Plotting learning curves with randomly selected examples
参考github
新建文件learningCurveWithRandomSel.m
function [error_train, error_val] = ...
learningCurveWithRandomSel(X, y, Xval, yval, lambda)
%LEARNINGCURVE Generates the train and cross validation set errors needed
%to plot a learning curve
% [error_train, error_val] = ...
% LEARNINGCURVE(X, y, Xval, yval, lambda) returns the train and
% cross validation set errors for a learning curve. In particular,
% it returns two vectors of the same length - error_train and
% error_val. Then, error_train(i) contains the training error for
% i examples (and similarly for error_val(i)).
%
% In this function, you will compute the train and test errors for
% dataset sizes from 1 up to m. In practice, when working with larger
% datasets, you might want to do this in larger intervals.
%
% Number of training examples
m = size(X, 1);
% You need to return these values correctly
error_train = zeros(m, 1);
error_val = zeros(m, 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in
% error_train and the cross validation errors in error_val.
% i.e., error_train(i) and
% error_val(i) should give you the errors
% obtained after training on i examples.
%
% Note: You should evaluate the training error on the first i training
% examples (i.e., X(1:i, :) and y(1:i)).
%
% For the cross-validation error, you should instead evaluate on
% the _entire_ cross validation set (Xval and yval).
%
% Note: If you are using your cost function (linearRegCostFunction)
% to compute the training and cross validation error, you should
% call the function with the lambda argument set to 0.
% Do note that you will still need to use lambda when running
% the training to obtain the theta parameters.
%
% Hint: You can loop over the examples with the following:
%
% for i = 1:m
% % Compute train/cross validation errors using training examples
% % X(1:i, :) and y(1:i), storing the result in
% % error_train(i) and error_val(i)
% ....
%
% end
%
% ---------------------- Sample Solution ----------------------
% X: m*(n+1)
% y: m*1
% Xval: k*(n+1)
% yval: k*1
k = size(Xval, 1);
for i=1:m,
ki = min(i,k);
sum_train_J = 0;
sum_val_J = 0;
for j=1:50,
% Randomly select i data
rand_indices = randperm(m);
X_sel = X(rand_indices(1:i), :);
y_sel = y(rand_indices(1:i), :);
[theta] = trainLinearReg(X_sel, y_sel, 1); % lambda=1
[J, grad] = linearRegCostFunction(X_sel, y_sel, theta, 0); % lambda=0
sum_train_J = sum_train_J + J;
rand_indices = randperm(k);
Xval_sel = Xval(rand_indices(1:ki), :);
yval_sel = yval(rand_indices(1:ki), :);
[J, grad] = linearRegCostFunction(Xval_sel, yval_sel, theta, 0); % lambda=0
sum_val_J = sum_val_J + J;
end;
error_train(i) = sum_train_J/50;
error_val(i) = sum_val_J/50;
end;
% -------------------------------------------------------------
% =========================================================================
end
ex5.m
%% 选做部分2:随机选择样本,计算误差,取平均值
lambda = 0.01;
[theta] = trainLinearReg(X_poly, y, lambda);
% Plot training data and fit
figure(1);
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
plotFit(min(X), max(X), mu, sigma, theta, p);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
title (sprintf('Polynomial Regression Fit (lambda = %f)', lambda));
figure(2);
[error_train, error_val] = ...
learningCurveWithRandomSel(X_poly, y, X_poly_val, yval, lambda);
plot(1:m, error_train, 1:m, error_val);
title(sprintf('Polynomial Regression Learning Curve (lambda = %f)', lambda));
xlabel('Number of training examples')
ylabel('Error')
axis([0 13 0 100])
legend('Train', 'Cross Validation')
fprintf('Polynomial Regression (lambda = %f)\n\n', lambda);
fprintf('# Training Examples\tTrain Error\tCross Validation Error\n');
for i = 1:m
fprintf(' \t%d\t\t%f\t%f\n', i, error_train(i), error_val(i));
end
fprintf('Program paused. Press enter to continue.\n');
pause;
测验2:Machine Learning System Design
第一题
第二题
第三题

答案
A
分析:
A:当阀值变为0.9时,查准率提高了,正确。
B:当阀值为0.5时,可以计算出F1值为0.5;当阀值为0.9时,F1变为0.18,下降了,错误。
C:阀值变为0.9时,查准率提高了,错误。
D:查全率(召回率)没有提高,错误。
第四题

答案
ACD
分析:
A:全部预测为y=0,则根据recall定义知,分子为0,故结果为0,正确。
B:全部预测为1,根据recall = TP/(TP+FN)知,FN为0,故recall为1,错误。
C:全部预测为1,由B知recall为1,即100%;根据precision = TP/(TP + FP)知,TP + FP = 100%且TP=1%,故precision=1%,正确。
D:依据题意,99%都是non spam,故正确。




