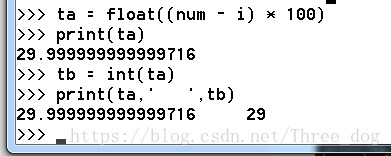
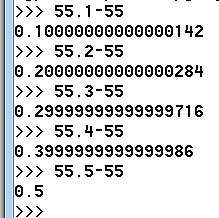
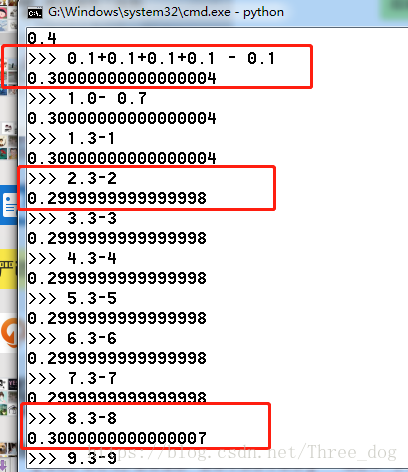
第一重境界,呆呆傻傻的遍历boolisPrime(intprime){for(intj=2;(j*j)usingnamespacestd;intisprime(intprime){intcount=2;for(inti=3;i<=prime;i++){boolflag=true;for(intj=2;(j*j)
不知起啥标题好
kingson____
你若不想做,总能找到借口;你若想做,总会找到方法。------阿拉伯谚语[^name]首先,吐槽下先,早上憋着憋着码了一上午,居然没发出去,然后退出了编辑去看发的文章,丫的没有,顿觉满世界充满敌意(别当真啦),后找退出前提示的保存为私密文章,找不到≥﹏≤压根不知在那里(新手来的,哪位大神知道麻烦告知小的一声)好啦吐槽完毕,进入正文话说一年前,我就有大神的博客资料(编程随想的chm文件)。可惜当时太
如何在Ubuntu上下载Firefox的ESR版本
一大加贝
Linux
Ubuntu是Linux操作系统的桌面类系统的一个发行版,因为网站后台是Linux操作系统,所以想着在虚拟机上装个Ubuntu系统学习一下。看了编程随想有关于浏览器的选择问题,Ta推荐Firefox。原因有以下几点:Firefox是开源软件,是由非营利组织的专门维护,这样就保证了Firefox的开发团队不会因为商业利益而拼了老命收集用户的隐私数据。与此截然相反的就是Google,因为他们是商业公司
Java新手的通病
youngster21
Programming
转自编程随想的博客:http://program-think.blogspot.com/2009/01/defect-of-java-beginner-0-overview.htmlJava新手的通病[0]:概述其实很早以前就想写这样一个文章,可惜当时我没有Blog,所以到现在才写下来。最近几年,随着Java在Web应用和企业应用两个方面的普及,对Java程序员的需求量大增。因此Java程序员的数
「不要随便做一个和事佬」写出我心(六十三)
Simle
不要随便做一个和事佬首发|微信公众号「编程随想曲」越长大,就会觉得做一个和事佬的机会越多,但是越长大,我们也会慢慢意识到,和事佬从一个褒义词,变为一个中性词,甚至有时候沦为贬义词。和事佬作为一个中间角色,如果你做不好,很容易造成“猪八戒照镜子,里外不是人”的后果。其次,和事佬本来就很难做好,多数情况我们是在十万火急的时候充当一个和事佬的角色,而这个时候我们对甲乙双方的真实情况了解甚少,因此很容易会
名人名言——摘录自编程随想的博客
weixin_34124651
1.一个人的价值,在于他贡献了什么,而不在于他获得了什么!——爱因斯坦2.你若喜爱你自己的价值,你就得给世界创造价值!——歌德3.我从来不把安逸和享乐当作生活目的;对这种伦理基础,我称之为【猪栏的理想】——爱因斯坦4.未经反思自省的人生不值得去过Theunexaminedlifeisnotworthliving.——苏格拉底(哲学之父)5.大多数人在20到30岁就已经过完自己的一生;一过了这个年龄
「看个电影,放松一下」写出我心(五十五)
Simle
看个电影,放松一下首发|微信公众号「编程随想曲」都说艺术来源于生活,高于生活,而影视作品是我们日常不可或缺的“艺术”,平时可能没有太多时间欣赏,周末一定要抽空看看,放松一下。电视剧有时候略显拖沓,而电影是很好选择,差不多一个半小时的时间,让我们领略不一样的旅程,亦或不一样的人生,亦或不一样的社会。喜剧片让我们开怀一笑,暂时忘记生活的烦恼。爱情片让我们感受婚姻,提前了解生活的柴米油盐。战争片让我们感
不抽耳光,不长记性
木鲸鱼
今天利用一天的时间仔细看了编程随想关于信息安全系列的扫盲文章,整个看得过程中总有种不解渴的感觉,这些文章都是12年左右写的,看着这些文字,脑子里不断在回忆自己当时在干嘛,想起了自己在刚进大学时报名竞选做网络部的学生干部。当时想去网络部的动机就是缘于自己对计算机有点点好奇,为什么一个小小的笔记本这么厉害,打开浏览器的时候,总是给我弹出广告,烦都烦死人了,是不是可以学点电脑知识,自己鼓捣一番就能做个纯
数字证书及 CA 的扫盲介绍
乃铭
版权声明作者编程随想本文原始地址:https://program-think.blogspot.com/2010/02/introduce-digital-certificate-and-ca.html最近1-2周(注:此文发布于2010年2月8日),关于CNNIC的CA证书问题,网上搞得沸沸扬扬。但是俺发觉,即使是一些IT行业的技术人员,也搞不太明白该问题的严重性(至于不懂技术的傻瓜用户,就更甭
“货币经济学”的基本概念:从“利率”到“央行货币政策”
清心涟漪
前言作者:编程随想原作者写作起源于8月初,人民币对美元的汇率破7。基于本人对金融学的理解,阅读完原文之后,做了部分精简和排版,以解释“货币经济学”的基本概念。本文的目标读者如果自认为对“宏观经济学”,尤其是其中的“货币经济学”已经有足够的认识,那么,本文你就不用看了。如果对这个领域还不熟悉,并且希望能对该领域有更系统性的了解,建议直接去看《货币金融学》这本书。这是非常经典的教材,被欧美很多高校采用
编程随想一二
初仔仔
最近看《程序员的思维修炼》,觉得其中有关右脑以及隐喻颇为有趣,故有了此篇随想...嘻嘻,貌似书中说的颇有道理。书写就像演讲一样,是个不错的思维工具。关于委托。貌似大家最爱说它是类型安全的函数指针,何为类型安全?自然是指GC这个奶妈托管的,指针自然不是托管的,也就是不是安全的类型。有位园友把GC比成体制,GC外就是体制外,真是精辟。既然不能在体制内,只要传递指针,那就是只能包成安全的,包装盒自然也就
求质数算法的N种境界 (N > 10)
sustxuguohao
经典题目
作者:编程随想本文原始地址:http://program-think.blogspot.com/2011/12/prime-algorithm-1.html★引子前天,俺在《俺的招聘经验[4]:通过笔试答题能看出啥?》一文,以”求质数”作为例子,介绍了一些考察应聘者的经验。由于本文没有政治敏感内容,顺便就转贴到俺在CSDN的镜像博客。昨天,某个CSDN网友在留言中写道:老实说,这个程序并不好写,除
编程随想
sinat_39173458
花了一点时间拜读了《c程序设计语言》书,作为一个初级程序员来讲,这本书表现得不太友好。但是内容却让我感到非常满意,里面提到的编程规范还有一些编程思想是非常值得我们学习的。代码的运算符之间要有空格,编写程序应该是从简单到复杂,不要妄想撸起袖子就可以写出一个大项目。编程这件事情可不能太急躁,慢慢来,欲速则不达,只有掌握了基础的知识点以后才会编出有质量的代码。有计划地去做一些CS计划,刷OJ或者acm之
学习技术的三部曲:WHAT、HOW、WHY(转)
东风三队
作者:编程随想原文地址:http://program-think.blogspot.com/2009/02/study-technology-in-three-steps.html最近几天有些网友在邮件里面问我关于学习的问题。有好几个人觉得工作了几年,也学会了不少的类库、框架、甚至语言,但是感觉自己的能力没有太大的提高。因此今天来说一下我个人对这方面的体会,希望对大伙儿(尤其是新手)有帮助。先声明
一、阅读的活力与艺术
puj0033
自从我在幼儿园咿咿呀呀学说话、识字、听、看故事开始,阅读就开始伴随我走过了三十个春秋。小时候我就是个重度的电视迷,电视机就是我的好朋友,小人书故事书就是我的开心果,结果长时间看电视直成为了我近视的主要原因,临近高考前才配了一副眼镜。我喜欢背诵唐诗宋词,甚至高中一字不差背过《岳阳楼记》,对诗词有特殊的爱好,爱看《中华好诗词》,好读书不求甚解。《如何阅读一本书》是从编程随想哥的博客里面看到的,后面随即
Java 新手入门需要关注的一些问题
luxixing
新手java
声明:本文所有列举的问题都来源于《编程随想》的博客,这个博客的博主知识渊博,编程方面的一些文章质量很高,给人醍醐灌顶的感觉。算法和数据结构什么时候该用数组类型容器,什么时候该用链表型容器,如何合理的使用数据类型什么是散列函数,HashMap的实现原理是什么什么是递归,使用递归实现目录树遍历什么是算法复杂度是否理解空间换时间的思想写一个针对整数数组的冒泡排序,写一个针对整数数组的二分查找函数面向对象
无处不在的二八原理
原理
无处不在的二八原理
2009-03-26 作者:编程随想 来源:编程随想的blog
什么是二八原理
我估计看我博客的人里面,应该有很多人听说过二八原理(如果你之前从来没听说过,那你的知识面有 太窄的嫌疑)。但是知道二八原理的人有很多却不会(或者不善于)运用。直接的后果就是你在各种事情上付出了很多时间与精力,但是回报却很少。鉴于该原理非 常非常的实用,
线程及 进程间的通信问题! .
线程
一个很好的编程随想的博客http://program-think.blogspot.com/2009/03/producer-consumer-pattern-0-overview.html
架构设计:生产者/消费者模式[0]:概述
1、如何确定数据单元2、队列缓冲区3、环形缓冲区4、双缓冲区 生产 消费 2010-06-01 10:13
#in
小狼毫输入法配置微软双拼以及模糊音定制
81蓝天
第一次看到小狼毫输入法是在编程随想的博客上,他推荐的输入法中排名第一个的就是小狼毫输入法,而且对其评价非常高。关于小狼毫输入法的讨论在这里,我只对自己目前需求比较关心的微软双拼以及模糊音,因为弄好这两点,我就可以正常使用了。下载并且我们安装完成后,以windows环境下为例,记录需要对它的安装文件修改的地方。1.切换到简体中文因为小狼毫输入法默认的是繁体中文输入,所以安装后的第一件事情是把输入法切
生产者消费者问题
zi413293813
方法:生产者消费者问题架构设计:生产者/消费者模式[0]:概述from编程随想的博客by编程随想今天打算来介绍一下“生产者/消费者模式”,这玩意儿在很多开发领域都能派上用场。由于该模式很重要,打算分几个帖子来介绍。今天这个帖子先来扫盲一把。如果你对这个模式已经比较了解,请跳过本帖子,直接看下一个帖子(关于如何确定数据单元)。看到这里,可能有同学心中犯嘀咕了:在四人帮(GOF)的23种模式里面似乎没
数字证书(转)
vga
数字证书及CA的扫盲介绍作者:编程随想 发布时间:2013-12-0311:48 阅读:1179次 推荐:11 原文链接 [收藏] ★先说一个通俗的例子考虑到证书体系的相关知识比较枯燥、晦涩。俺先拿一个通俗的例子来说事儿。◇普通的介绍信想必大伙儿都听说过介绍信的例子吧?假设A公司的张三先生要到B公司去拜访,但是B公司的所有人都不认识他,他咋办捏?常用的办法是带公司开的一张介绍信,在信中
线程及 进程间的通信问题!
jtop0
thread多线程windowsobjectSemaphore编译器
一个很好的编程随想的博客http://program-think.blogspot.com/2009/03/producer-consumer-pattern-0-overview.html架构设计:生产者/消费者模式[0]:概述 1、如何确定数据单元2、队列缓冲区3、环形缓冲区4、双缓冲区生产消费2010-06-0110:13#include#include#include#includetem
有没有这个必要
bibodeng
职场休闲随便写写
2011年8月14日 bibodeng 今天上网看了一下订阅的博客,结果发现“编程随想”的博客居然可以毫无阻碍地访问,真是奇了个怪。不管那么多,还是先看再说吧。 在博客里面,看到了许多指导同学们怎样成为优秀开发人员的,还有怎样找书、自学的。真是很符合我们这些刚入门的人的口味,而且还有心理学、思维方面的文章。现在,不知道我做的那个暑假实践还有没有必要。看来是没有必要了,被师兄说中了。互联网的
有没有这个必要
bibodeng
职场休闲随便写写生活感悟
2011年8月14日bibodeng今天上网看了一下订阅的博客,结果发现“编程随想”的博客居然可以毫无阻碍地访问,真是奇了个怪。不管那么多,还是先看再说吧。在博客里面,看到了许多指导同学们怎样成为优秀开发人员的,还有怎样找书、自学的。真是很符合我们这些刚入门的人的口味,而且还有心理学、思维方面的文章。现在,不知道我做的那个暑假实践还有没有必要。看来是没有必要了,被师兄说中了。互联网的时代真是要什么
设计模式介绍
tntxia
设计模式
设计模式来源于土木工程师 克里斯托弗 亚历山大(http://en.wikipedia.org/wiki/Christopher_Alexander)的早期作品。他经常发表一些作品,内容是总结他在解决设计问题方面的经验,以及这些知识与城市和建筑模式之间有何关联。有一天,亚历山大突然发现,重复使用这些模式可以让某些设计构造取得我们期望的最佳效果。
亚历山大与萨拉-石川佳纯和穆雷 西乐弗斯坦合作
android高级组件使用(一)
百合不是茶
androidRatingBarSpinner
1、自动完成文本框(AutoCompleteTextView)
AutoCompleteTextView从EditText派生出来,实际上也是一个文本编辑框,但它比普通编辑框多一个功能:当用户输入一个字符后,自动完成文本框会显示一个下拉菜单,供用户从中选择,当用户选择某个菜单项之后,AutoCompleteTextView按用户选择自动填写该文本框。
使用AutoCompleteTex
[网络与通讯]路由器市场大有潜力可挖掘
comsci
网络
如果国内的电子厂商和计算机设备厂商觉得手机市场已经有点饱和了,那么可以考虑一下交换机和路由器市场的进入问题.....
这方面的技术和知识,目前处在一个开放型的状态,有利于各类小型电子企业进入
&nbs
自写简单Redis内存统计shell
商人shang
Linux shell统计Redis内存
#!/bin/bash
address="192.168.150.128:6666,192.168.150.128:6666"
hosts=(${address//,/ })
sfile="staticts.log"
for hostitem in ${hosts[@]}
do
ipport=(${hostitem
单例模式(饿汉 vs懒汉)
oloz
单例模式
package 单例模式;
/*
* 应用场景:保证在整个应用之中某个对象的实例只有一个
* 单例模式种的《 懒汉模式》
* */
public class Singleton {
//01 将构造方法私有化,外界就无法用new Singleton()的方式获得实例
private Singleton(){};
//02 申明类得唯一实例
priva
springMvc json支持
杨白白
json springmvc
1.Spring mvc处理json需要使用jackson的类库,因此需要先引入jackson包
2在spring mvc中解析输入为json格式的数据:使用@RequestBody来设置输入
@RequestMapping("helloJson")
public @ResponseBody
JsonTest helloJson() {
android播放,掃描添加本地音頻文件
小桔子
最近幾乎沒有什麽事情,繼續鼓搗我的小東西。想在項目中加入一個簡易的音樂播放器功能,就像華為p6桌面上那麼大小的音樂播放器。用過天天動聽或者QQ音樂播放器的人都知道,可已通過本地掃描添加歌曲。不知道他們是怎麼實現的,我覺得應該掃描設備上的所有文件,過濾出音頻文件,每個文件實例化為一個實體,記錄文件名、路徑、歌手、類型、大小等信息。具體算法思想,
oracle常用命令
aichenglong
oracledba常用命令
1 创建临时表空间
create temporary tablespace user_temp
tempfile 'D:\oracle\oradata\Oracle9i\user_temp.dbf'
size 50m
autoextend on
next 50m maxsize 20480m
extent management local
25个Eclipse插件
AILIKES
eclipse插件
提高代码质量的插件1. FindBugsFindBugs可以帮你找到Java代码中的bug,它使用Lesser GNU Public License的自由软件许可。2. CheckstyleCheckstyle插件可以集成到Eclipse IDE中去,能确保Java代码遵循标准代码样式。3. ECLemmaECLemma是一款拥有Eclipse Public License许可的免费工具,它提供了
Spring MVC拦截器+注解方式实现防止表单重复提交
baalwolf
spring mvc
原理:在新建页面中Session保存token随机码,当保存时验证,通过后删除,当再次点击保存时由于服务器端的Session中已经不存在了,所有无法验证通过。
1.新建注解:
? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
《Javascript高级程序设计(第3版)》闭包理解
bijian1013
JavaScript
“闭包是指有权访问另一个函数作用域中的变量的函数。”--《Javascript高级程序设计(第3版)》
看以下代码:
<script type="text/javascript">
function outer() {
var i = 10;
return f
AngularJS Module类的方法
bijian1013
JavaScriptAngularJSModule
AngularJS中的Module类负责定义应用如何启动,它还可以通过声明的方式定义应用中的各个片段。我们来看看它是如何实现这些功能的。
一.Main方法在哪里
如果你是从Java或者Python编程语言转过来的,那么你可能很想知道AngularJS里面的main方法在哪里?这个把所
[Maven学习笔记七]Maven插件和目标
bit1129
maven插件
插件(plugin)和目标(goal)
Maven,就其本质而言,是一个插件执行框架,Maven的每个目标的执行逻辑都是由插件来完成的,一个插件可以有1个或者几个目标,比如maven-compiler-plugin插件包含compile和testCompile,即maven-compiler-plugin提供了源代码编译和测试源代码编译的两个目标
使用插件和目标使得我们可以干预
【Hadoop八】Yarn的资源调度策略
bit1129
hadoop
1. Hadoop的三种调度策略
Hadoop提供了3中作业调用的策略,
FIFO Scheduler
Fair Scheduler
Capacity Scheduler
以上三种调度算法,在Hadoop MR1中就引入了,在Yarn中对它们进行了改进和完善.Fair和Capacity Scheduler用于多用户共享的资源调度
2. 多用户资源共享的调度
Nginx使用Linux内存加速静态文件访问
ronin47
Nginx是一个非常出色的静态资源web服务器。如果你嫌它还不够快,可以把放在磁盘中的文件,映射到内存中,减少高并发下的磁盘IO。
先做几个假设。nginx.conf中所配置站点的路径是/home/wwwroot/res,站点所对应文件原始存储路径:/opt/web/res
shell脚本非常简单,思路就是拷贝资源文件到内存中,然后在把网站的静态文件链接指向到内存中即可。具体如下:
关于Unity3D中的Shader的知识
brotherlamp
unityunity资料unity教程unity视频unity自学
首先先解释下Unity3D的Shader,Unity里面的Shaders是使用一种叫ShaderLab的语言编写的,它同微软的FX文件或者NVIDIA的CgFX有些类似。传统意义上的vertex shader和pixel shader还是使用标准的Cg/HLSL 编程语言编写的。因此Unity文档里面的Shader,都是指用ShaderLab编写的代码,然后我们来看下Unity3D自带的60多个S
CopyOnWriteArrayList vs ArrayList
bylijinnan
java
package com.ljn.base;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
import java.util.concurrent.CopyOnWriteArrayList;
/**
* 总述:
* 1.ArrayListi不是线程安全的,CopyO
内存中栈和堆的区别
chicony
内存
1、内存分配方面:
堆:一般由程序员分配释放, 若程序员不释放,程序结束时可能由OS回收 。注意它与数据结构中的堆是两回事,分配方式是类似于链表。可能用到的关键字如下:new、malloc、delete、free等等。
栈:由编译器(Compiler)自动分配释放,存放函数的参数值,局部变量的值等。其操作方式类似于数据结构中
回答一位网友对Scala的提问
chenchao051
scalamap
本来准备在私信里直接回复了,但是发现不太方便,就简要回答在这里。 问题 写道 对于scala的简洁十分佩服,但又觉得比较晦涩,例如一例,Map("a" -> List(11,111)).flatMap(_._2),可否说下最后那个函数做了什么,真正在开发的时候也会如此简洁?谢谢
先回答一点,在实际使用中,Scala毫无疑问就是这么简单。
mysql 取每组前几条记录
daizj
mysql分组最大值最小值每组三条记录
一、对分组的记录取前N条记录:例如:取每组的前3条最大的记录 1.用子查询: SELECT * FROM tableName a WHERE 3> (SELECT COUNT(*) FROM tableName b WHERE b.id=a.id AND b.cnt>a. cnt) ORDER BY a.id,a.account DE
HTTP深入浅出 http请求
dcj3sjt126com
http
HTTP(HyperText Transfer Protocol)是一套计算机通过网络进行通信的规则。计算机专家设计出HTTP,使HTTP客户(如Web浏览器)能够从HTTP服务器(Web服务器)请求信息和服务,HTTP目前协议的版本是1.1.HTTP是一种无状态的协议,无状态是指Web浏览器和Web服务器之间不需要建立持久的连接,这意味着当一个客户端向服务器端发出请求,然后We
判断MySQL记录是否存在方法比较
dcj3sjt126com
mysql
把数据写入到数据库的时,常常会碰到先要检测要插入的记录是否存在,然后决定是否要写入。
我这里总结了判断记录是否存在的常用方法:
sql语句: select count ( * ) from tablename;
然后读取count(*)的值判断记录是否存在。对于这种方法性能上有些浪费,我们只是想判断记录记录是否存在,没有必要全部都查出来。
对HTML XML的一点认识
e200702084
htmlxml
感谢http://www.w3school.com.cn提供的资料
HTML 文档中的每个成分都是一个节点。
节点
根据 DOM,HTML 文档中的每个成分都是一个节点。
DOM 是这样规定的:
整个文档是一个文档节点
每个 HTML 标签是一个元素节点
包含在 HTML 元素中的文本是文本节点
每一个 HTML 属性是一个属性节点
注释属于注释节点
Node 层次
jquery分页插件
genaiwei
jqueryWeb前端分页插件
//jquery页码控件// 创建一个闭包 (function($) { // 插件的定义 $.fn.pageTool = function(options) { var totalPa
Mybatis与Ibatis对照入门于学习
Josh_Persistence
mybatisibatis区别联系
一、为什么使用IBatis/Mybatis
对于从事 Java EE 的开发人员来说,iBatis 是一个再熟悉不过的持久层框架了,在 Hibernate、JPA 这样的一站式对象 / 关系映射(O/R Mapping)解决方案盛行之前,iBaits 基本是持久层框架的不二选择。即使在持久层框架层出不穷的今天,iBatis 凭借着易学易用、
C中怎样合理决定使用那种整数类型?
秋风扫落叶
c数据类型
如果需要大数值(大于32767或小于32767), 使用long 型。 否则, 如果空间很重要 (如有大数组或很多结构), 使用 short 型。 除此之外, 就使用 int 型。 如果严格定义的溢出特征很重要而负值无关紧要, 或者你希望在操作二进制位和字节时避免符号扩展的问题, 请使用对应的无符号类型。 但是, 要注意在表达式中混用有符号和无符号值的情况。
&nbs
maven问题
zhb8015
maven问题
问题1:
Eclipse 中 新建maven项目 无法添加src/main/java 问题
eclipse创建maevn web项目,在选择maven_archetype_web原型后,默认只有src/main/resources这个Source Floder。
按照maven目录结构,添加src/main/ja
(二)androidpn-server tomcat版源码解析之--push消息处理
spjich
javaandrodipn推送
在 (一)androidpn-server tomcat版源码解析之--项目启动这篇中,已经描述了整个推送服务器的启动过程,并且把握到了消息的入口即XmppIoHandler这个类,今天我将继续往下分析下面的核心代码,主要分为3大块,链接创建,消息的发送,链接关闭。
先贴一段XmppIoHandler的部分代码
/**
* Invoked from an I/O proc
用js中的formData类型解决ajax提交表单时文件不能被serialize方法序列化的问题
中华好儿孙
JavaScriptAjaxWeb上传文件FormData
var formData = new FormData($("#inputFileForm")[0]);
$.ajax({
type:'post',
url:webRoot+"/electronicContractUrl/webapp/uploadfile",
data:formData,
async: false,
ca
mybatis常用jdbcType数据类型
ysj5125094
mybatismapperjdbcType
MyBatis 通过包含的jdbcType
类型
BIT FLOAT CHAR