【机器学习详解】SVM解回归问题

1.方法分析

在样本数据集(xn,tn)(xn,tn)中，tntn不是简单的离散值，而是连续值。如在线性回归中，预测房价的问题。与线性回归类似，目标函数是正则平方误差函数：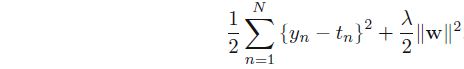

在SVM回归算法中，目的是训练出超平面y=wTx+by=wTx+b，采用yn=wTxn+byn=wTxn+b作为预测值。为了获得稀疏解，即计算超平面参数w,bw,b不依靠所有样本数据，而是部分数据（如在SVM分类算法中，支持向量的定义），采用ϵ−insensitiveϵ−insensitive 误差函数–Vapnik,1995。
ϵ−insensitiveϵ−insensitive 误差函数定义为，如果预测值ynyn与真实值tntn的差值小于阈值ϵϵ将不对此样本点做惩罚，若超出阈值，惩罚量为|yn−tn|−ϵ|yn−tn|−ϵ。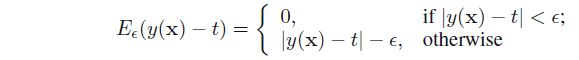

下图为ϵ−insensitiveϵ−insensitive 误差函数与平方误差函数的图形

2.目标函数

观察上述的EϵEϵ 误差函数的形式,可以看到，实际形成了一个类似管道的样子，在管道中样本点，不做惩罚，所以被称为ϵ−tubeϵ−tube，如下图阴影红色部分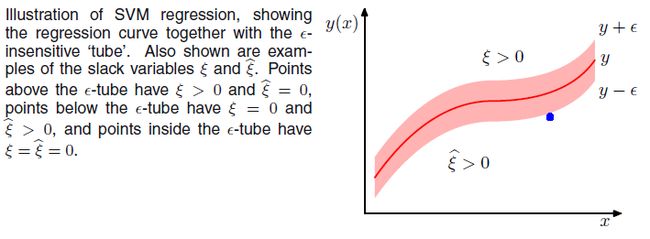

采用EϵEϵ替代平方误差项，因此可以定义最小化误差函数作为优化目标：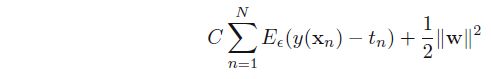

由于上述目标函数含有绝对值项不可微。我们可以转化成一个约束优化问题，常用的方法是为每一个样本数据定义两个松弛变量ξn≥0,ξn^≥0ξn≥0,ξn^≥0，表示度量tntn与ϵ−tubeϵ−tube的距离。
如上图所示：
当样本点真实值tntn位于管道上方时，ξn>0ξn>0,写成表达式：tn>y(xn)+ϵtn>y(xn)+ϵ时，ξn>0，ξ^n=0ξn>0，ξ^n=0；
当样本点真实值tntn位于管道下方时，ξn^>0ξn^>0,写成表达式：tn0，ξn=0ξn^>0，ξn=0；
因此使得每个样本点位于管道内部的条件为：
当tntn位于管道上方时，ξn>0ξn>0，有tn−y(xn)−ξn≤ϵtn−y(xn)−ξn≤ϵ
当tntn位于管道下方时，ξn^>0ξn^>0，有y(xn)−tn−ξ^n≤ϵy(xn)−tn−ξ^n≤ϵ
误差函数可以写为一个凸二次优化问题：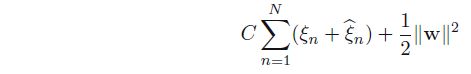

约束条件：
ξn≥0ξn≥0
ξn^≥0ξn^≥0
tn−y(xn)−ξn≤ϵtn−y(xn)−ξn≤ϵ
y(xn)−tn−ξ^n≤ϵy(xn)−tn−ξ^n≤ϵ
写成拉格朗日函数：

3.对偶问题

上述问题为极小极大问题：minw,b,ξn,ξn^ maxμn,μn^,αn,αn^Lminw,b,ξn,ξn^ maxμn,μn^,αn,αn^L与SVM分类分析方法一样，改写成对偶问题maxμn,μn^,αn,αn^ minw,b,ξn,ξn^Lmaxμn,μn^,αn,αn^ minw,b,ξn,ξn^L；首先分别对w,b,ξn,ξn^w,b,ξn,ξn^求偏导数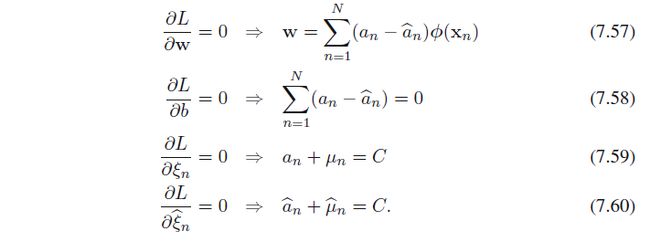

带回到拉格朗日函数中，化简得到只关于αn,αn^αn,αn^的函数，目标即最大化此函数。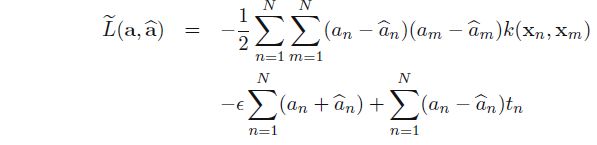

约束条件为：
0≤αn≤C0≤αn≤C
0≤αn^≤C0≤αn^≤C,其中k(xn,xm)=(xn)Txmk(xn,xm)=(xn)Txm为向量内积。
下面考虑KKT条件：

由式7.65,7.66知：
当αn≠0αn≠0时，必有ϵ+ξn+y(xn)−tn=0ϵ+ξn+y(xn)−tn=0,这些点位于管道上方边界出，或者管道上面。
当α^n≠0α^n≠0时，必有ϵ+ξn−y(xn)+tn=0ϵ+ξn−y(xn)+tn=0,这些点位于管道下方边界出，或者管道下面。
同时，由式7.65,7.66知，对于任意一个数据点，由于ϵ>0ϵ>0，则αn，α^nαn，α^n不可能同时不为0，而且得到在管道内部的点，必然有αn=0，α^n=0αn=0，α^n=0。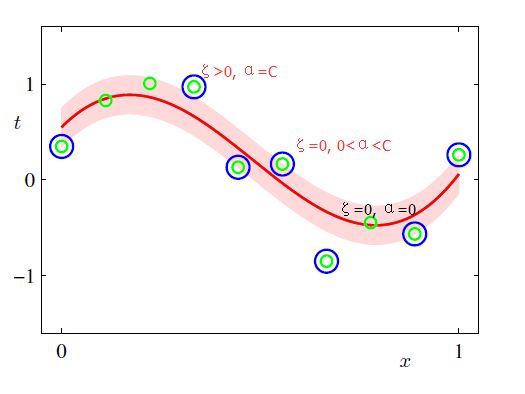

4.超平面计算：

把ww表达式带入到y=wTx+by=wTx+b得：

由上述的分析，影响超平面参数的点为位于管道边界处，或者管道外面。
关于b的计算，可以考虑在管道上方边界处一个点必然有：
ξn=0ξn=0
ϵ+ξn+y(xn)−tn=0ϵ+ξn+y(xn)−tn=0
联立解出：